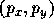. A
point p in S is maximal if there is no other point
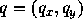in S such that 
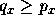and 
.
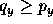(In other words, there is no other point in S that is
simultaneously east and north of q.)
An important part of designing computer networks is protecting information from being read by someone other than the indented recipient. A common way to solve this problem is to encrypt the information so that it looks like gibberish.
A simple way to encrypt information is called a Caesar cypher (because Julius Caesar was the first to use it). In a Caesar cypher, a number between 0 and 25 is selected as the key for the message. Each letter (but not spaces, numbers, or punctuation) is shifted by the key. For example, if the key is 1 and original letter is 'A', the encrypted letter is 'B'.
Write a program to encrypt a message using a Caesar cypher.
The first line of the input will be an integer (from 0 to 25), which will be the key. The rest of the input will be lines that contain the message to encrypt. Each of the remaining lines will contain less than 100 characters. Your program should stop when a line contains the word STOP
Input:
1 The quick brown fox jumped over the lazy dogs numbers and other things 1, 2, and 3! STOPOutput:
Uif rvjdl cspxo gpy kvnqfe pwfs uif mbaz epht ovncfst boe puifs uijoht 1, 2, boe 3!
Let S be a set of points in the plane. Each point p is
represented by its x and y coordinates, 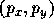. A
point p in S is maximal if there is no other point
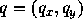in S such that 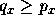and .
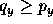(In other words, there is no other point in S that is
simultaneously east and north of q.)
Layer 1 consists of the points that are maximal in S. Layer
2 consists of the points that are maximal in S, excluding
layer 1. In general, each layer consists of the points that
are maximal in S excluding all the previous layers. For
example, in the figure below, Layer 1 consists of points
, 
, 
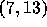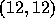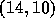, and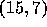 
.
Write a program that computes all the layers of a point set.
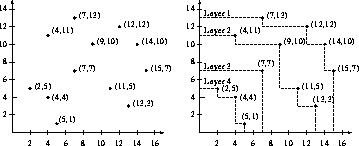
Each line of the input contains two numbers, the x and y coordinates of a single point. You may assume that the coordinates are integers in the range from 1 to 99 and that there are at most 200 points. Some points may share the same x-coordinate, and some may share the same y-coordinate, but you may assume that there are no duplicate points (two or more points with both the same x- and y-coordinates).
Output the points lying on each layer, with one line for each layer, starting with layer 1. On each line of output first print the layer number, followed by a colon (`` :''), followed by the list of points lying lying on this layer. The coordinates of each point are enclosed in parentheses, as shown in the examples below. Output points within each level in order of increasing x-coordinate.
Input:
5 1 14 10 7 7 9 10 12 12 11 5 4 4 15 7 4 11 7 13 2 5 13 3
Output:
1: ( 7,13) (12,12) (14,10) (15,7) 2: ( 4,11) ( 7,10) (11, 5) (13,3) 3: ( 7, 7) 4: ( 2, 5) ( 4, 4) ( 5, 1)
A 2-dimensional matrix is said to be monotone if as you read any row from left to right the values either remain constant or increase (they NEVER decrease), and as you read any column from top to bottom its values either remain constant or increase. A submatrix is a rectangular region of a matrix consisting of consecutive rows and columns. The size of a submatrix is its number of elements.
Write a program that, given a matrix, computes the monotone submatrix having the largest number of elements. If there are ties for the largest, then you may output any one of them.
The first line of the input contains two numbers, the number of rows and the number of columns in the matrix. Each subsequent line contains one row of the matrix. The matrix values are integers in the range from 0 to 99. You may assume that there are no more than 100 rows and 100 columns.
Output the submatrix one row per line, with each number separated by one or more spaces.
Input:
4 5 2 4 4 8 8 1 4 5 10 9 7 9 8 13 17 10 11 14 15 16
Output:
4 8 5 10 8 13 14 15
Input:
4 5 2 4 4 8 8 4 4 5 10 11 7 9 12 13 15 10 11 14 15 16
Output:
2 4 4 8 8 4 4 5 10 11 7 9 12 13 15 10 11 14 15 16
Input:
5 6 2 0 5 4 8 7 1 2 4 6 8 14 0 4 7 8 10 12 4 8 8 10 13 15 6 6 10 12 11 16
Output:
2 4 6 8 4 7 8 10 8 8 10 13
In a computer system, a deadlock occurs when a group of two or more programs are all blocked waiting for resources (e.g. disks, tape drives) that another member of the group is using. When a group of programs deadlock, no program in the group can make forward progress. Write a program to detect when a system contains a deadlock. Note: just because a request made by a program can't immediately be satisfied, it does not mean the system is deadlocked (see Example 1).
The input to the program consists of requests by programs to either acquire or release a resource. Each line will contain three values (each separated by a single space), an integer indicating the identity of the program making the request, a character indicating if the request is to acquire or release the resource (`a' or `r' respectively), and a string for the name of the resource.
When a deadlock is detected, your program should print the programs that are deadlocked. The list of programs involved in the deadlock should be sorted in increasing order of program identifier. Your program should terminate when a deadlock is found (and not read any additional input). If the end of input is reached, and no deadlock has been detected, your program should print "No deadlocks found". If an error is found (such as a program trying to acquire a resource it already has), your program should print "Input Error" and terminate.
Input:
1 a disk 2 a disk 1 r disk 2 r disk -1 a empty
Output:
No deadlocks found
Input:
3 a mouse 1 a disk 2 a tape 1 a tape 2 a disk -1 r empty
Output:
Deadlock detected: 1 2
Write a program that outputs all sentences that are anagrams of the input sentence using only words from the supplied dictionary. For sentence to be a valid anagram, it must use all of the letters in the input sentence exactly once.
The first line is a sentence. The remaining lines are the words of a dictionary, entered one word per line. Other than the spaces appearing between words of the first line, the input will consist only of lower-case alphabetic symbols (`a'--`z').
All words will be no more than 10 characters long. There will be at most 5 words on the first line and no more than 20 lines after that (each of which contain one word).
You must print all combinations of words from the dictionary that are anagrams of the first sentence. For example, ``Raining Mad Fangs" is an anagram of ``Finding Anagrams''. For each combination of words, you don't have to print them our in every possible order. You may may only use each word from the dictionary once per anagram. However, the same word may appear multiple times in the dictionary.
If no anagrams are possible from the input sentence, your program should print "No anagrams for this sentence".
Input:
finding anagrams admiring afar drama fan fans fangs mad minding nag race rain quick raining signing soup
Output:
admiring fans nag drama fan signing fangs mad raining
Your input is a series of rectangles, one per line. Each rectangle is specified as two points (X,Y) that specify the opposite corners of a rectangle. All coordinates will be integers in the range 0 to 100. For example, the line
5 8 7 10specifies the rectangle who's corners are (5,8), (7,8), (7,10), (5,10).
If drawn on graph paper, that rectangle would cover four squares.
Your job is to count the number of
unit (i.e.,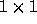 
) squares that are covered by
any one of the rectangles given as input. Any
square covered by more than one rectangle should only be counted once.
The input format is a series of lines, each containing 4 integers. Four -1's are used to separate problems, and four -2's are used to end the last problem. Otherwise, the numbers are the x-y coordinates of two points that are opposite corners of a rectangle.
Your output should be the number of squares covered by each set of rectangles. Each number should be printed on a separate line.
Input:
5 8 7 10 6 9 7 8 6 8 8 11 -1 -1 -1 -1 0 0 100 100 50 75 12 90 39 42 57 73 -2 -2 -2 -2Output:
8 10000
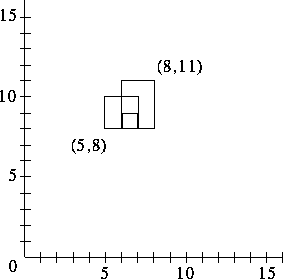
The three rectangles in the first probelem of the sample input.
Your input is in the form of an (X,Y) query point and n pairs of (X,Y) points. All numbers are integers.
The n points define a convex polygon. You must determine whether the query point is inside, outside, or on the border of the polygon.
Here are two sample poloygons, the one on the left is not convex, the one on the right is convex.
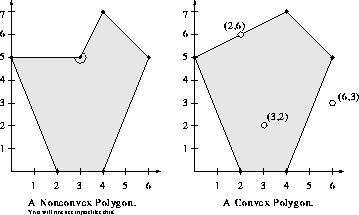
A number of lines consists of pairs of integers. The first pair of integers is the query point. All other pairs of integers specify vertices of the convex polygon.
For each input line print one line consisting of the query point followed by the string ``inside'', ``outside'', or ``border''.
Input:
5 5 0 0 10 0 0 10 10 10 5 15 0 0 10 0 0 10 10 10 0 5 0 0 10 0 0 10 10 10 3 2 0 5 2 0 4 0 6 5 4 7
Output:
5 5 inside 5 15 outside 0 5 boundary 3 2 inside
Consider the problem of computing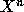 
with the fewest number of
multiplications, where X is a symbolic variable, which may take on any
numeric value, and n is a positive integer. Assume you can
multiply by X and any partial value previously computed
for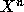 
.
A simple method is to start with X as the partial result, then multiply by X (n-1) times. More powerful algorithms can use many fewer numbers of multiplies (one such method is described in the Hindu classic Chandah-sutra, 200 BC).
Your goal is to design and implement an algorithm that can
compute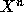 
for integer values of n within the number of
multiplies listed in the table below.
Notice that the simple algorithm that requires n-1 multiplies is not
sufficient, you must come up with a better algorithm.
There is no one right answer to this question.
For the purposes of judging the problem correct, any algorithm that
uses no more than the number of multiplies listed in the table is fine.
(Note: a fair bit of research has been done come up with an algorithm that
performs the minimum number of multiplies.
For example, for n = 23, 6 multiplies are sufficient).
You program should read a list of integers, one per line. Each integer will be between 1 and 10000. An input value of -1 will signal the end of input.
For each input value of n, print: n, the number of multiplies required to
calculate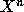 
, and the sequence of
multiplications required (separated by semicolons).
The sequence of multiplications
should be in the form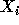 
= 
* 
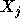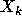, where 
.
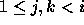The sequence starts with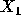 
. 
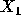= X is assumed by default.
Input:
1 -1Output:
1 0
Input:
3 14 -1Output:
3 2 X2 = X1 * X1; X3 = X2 * X1; 14 5 X2 = X1 * X1; X3 = X2 * X1; X4 = X3 * X3; X5 = X4 * X1; X6 = X5 * X5;