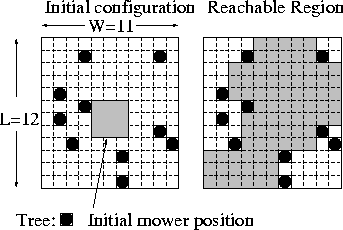
Suppose that you have a rectangular field that is L meters long and W meters wide. Let us think of this as an L by W grid of squares, where each square is 1 meter by 1 meter. Some of these squares have trees growing within them (shown as black circles in the figure below).
Your have a 
meter square lawn mower. You may move this
lawn mower up, down, left, or right by one meter so long as: (1) the
lawn mower lies entirely within the rectangular field, and (2) the
lawn mower never overlaps a square containing a tree. The lawn mower
cannot be rotated and cannot be picked up and moved over
a tree.
The lawn mower can ``reach'' a grid square if there is some way to move the lawn mower from its original position so that it entirely covers this square. Your task is to determine which squares of the lawn can be reached by the lawn mower. This region is shaded in the figure above on the right.
The first line of the input contains two positive integers, the length and width, L and W of the field. You may assume that length and width are at most 40. Each of the next L lines contains W marker characters, where each marker character corresponds to a grid square.
The marker character `+' means that there is a tree here, `.' means no tree. `M' is the center of the initial position of the lawn mower. (So initially the lawn mower overlaps this square and the 8 squares immediately surrounding it.) You may assume that there is exactly one `M', and initially the lawn mower is in a legal position (that is, it does not overlap any trees).
To aid readability, each marker character is preceded by a single space.
The output consists of L lines, each containing W marker characters, and each marker character is preceded by a single space. The character `+' signifies a tree, `O' (capital letter `Oh') is a square that the lawn mower can touch, and `.' is a square that the lawn mower cannot reach. The input and output for the above example is given below.
| Input: | Output: |
|---|---|
12 11 . . . . . . . . . . . . . . + . . . . . + . . . . . . . . . . . . . . . . . . . . . . . . + . . . . . . . . . . . . + . . . . . . . . + . . . M . . . . . . . . . . . . . . + . . . + . . . . . . . + . . . . . . + . . . . . . . . . . . . . . . . . . . . . + . . . . |
12 11 . . . . O O O O O . . . . . + O O O O O + . . . O O O O O O O O O . . O O O O O O O O O . + O O O O O O O O O . . . + O O O O O O O . + . O O O O O O O O . . . O O O O O O + . . . + O O O O O O . + O O O O O O + . . . . O O O O O O . . . . . O O O O O O + . . . . |
| Input 1 | Output 1 |
|---|---|
| Input 2 | Output 2 |
| Input 3 | Output 3 |
| Input 4 | Output 4 |
| Input 5 | Output 5 |