Notes
1 August 28, 2017
Audio and video capture from today’s class is available here.
2 August 30, 2017
Audio and video capture from today’s class is available here.
Code from today’s lecture:
3 September 1, 2017
Audio and video capture from today’s class is available here.
Code from today’s lecture:
4 September 6, 2017
Landing a RKT in BSL
We’re trying to land a rocket (RKT) safely on the ground. (See HtDP2e’s prologue for the original treatment.) We’re doing that with 2htdp/{image,universe} in the Beginning Student Language (BSL).
Drawing a RKT
First, we’ll draw a small rocket and name it RKT.
; A nifty rocket (define RKT (overlay/offset (overlay/offset (triangle 18 'solid "red") 0 27 (ellipse 24 60 'solid "gray")) 0 10 (isosceles-triangle 60 24 'solid "black")))
The identifier uses all capitals to indicate that RKT is a defined constant. Let’s draw a few example frames from our animation by placing RKT on an empty scene 100px wide and 200px high.
> (place-image RKT 0 0 (empty-scene 100 200))
The library function place-image requires the X/Y pixel offset from the first image to the second image, but placing RKT at 0,0 cuts off 3/4 of the rocket. Let’s move the rocket to the center of the scene by changing the X offset to 50.
> (place-image RKT 50 0 (empty-scene 100 200))
Now we’ll try to find the proper Y offset to place the rocket at the bottom of the scene.
> (place-image RKT 50 200 (empty-scene 100 200)) ; too far
> (place-image RKT 50 150 (empty-scene 100 200)) ; not far enough
> (place-image RKT 50 166 (empty-scene 100 200)) ; looks OK
If we adjust where we place RKT by -34px (from 200 to 166), the edge looks just about right. Copying and pasting is getting annoying, so let’s make a function that will do most of the work for us. We want to define a function that can draw our rocket for use in animate, so let’s call it draw-rocket.
Drawing RKT, Where?
We will land our rocket with animate. The signature of animate looks a little more complex than we’re used to seeing.
; (animate create-image) → natural-number/c ; create-image : (-> natural-number/c scene?)
We can write this in a slightly more familiar form:
; A Natural is a non-negative integer: one of { 0, 1, 2, ... }. ; animate : (Natural -> Image) -> Natural
The function animate expects a function as its input. The given function must have the signature Natural -> Image. So, we need to implement a function land-rocket with that signature.
What should we do with the natural number? We’re generalizing the expression (place-image RKT 50 0 (empty-scene 100 200)) and there are four obvious places we could use the natural number n: the X/Y offsets and the scene width/height.
We want the rocket to land–move from the top of the scene to bottom–which means changing where we place RKT vertically on the empty scene. We can do that by changing the Y offset given to place-image and test our example frames.
; land-rocket : Natural -> Image ; Draw a rocket on an empty scene with the y-offset N. (define (land-rocket n) (place-image RKT 50 n (empty-scene 100 200)))
> (land-rocket 0)
> (land-rocket 66)
> (land-rocket 166)
The first example with n equal to 0 has the rocket partially on the scene, but our landing animation should not start with any of the rocket visible. We should be able to use the same adjustment as earlier (-34px) to draw the rocket just above the top of the scene.
> (land-rocket -34)
Hmm, that left a few pixels hanging, so we must have gotten the original adjustment wrong. After a bit more trial and error, adjusting by -36px seems to be correct.
> (land-rocket -36)
There are two problems here.
First, and despite the fact that no errors occurred and images were returned, we broke land-rocket’s contract by applying it to negative integers.
Second, it would be tedious to perform this pixel adjustment each time we apply the function land-rocket. Instead, we can perform that adjustment inside the definition of land-rocket/v2 (and again test our examples).
; land-rocket/v2 : Natural -> Image ; Draw a rocket on an empty scene with the adjusted y-offset N. (define (land-rocket/v2 n) (place-image RKT 50 (- n 36) (empty-scene 100 200))) (land-rocket/v2 0) (land-rocket/v2 100) (land-rocket/v2 200)
Fantastic, let’s see how the animation looks!
Landing the RKT
> (animate land-rocket/v2)
Uh-oh. The rocket starts off correctly, but plows right through the bottom of the scene. After about (/ 200 28) seconds, the rocket begins to pass below the scene’s bottom edge.
So, how can we fix this?
A1: Is there some a stop-animate function we can call to stop the animation after the right amount of time?
R1: No, and it’s not obvious where to use such a function even if there were. Per its documentation, starting at 0 animate applies land-rocket/v2 to each successive natural number 28 times per second. Only after we close the animation’s window does the application of the animate function return the most recent (and highest) natural number. So, any (stop-animate (/ 200 28)) following our application of animate would not be evaluated until after the animation has ended.
A2: Couldn’t we call the hypothetical stop-animate inside of land-rocket/v2?
R2: Yes, but such a function would have to be performing side effects, which we’ll be discussing in more depth late this semester and next semester. It would require indirect communication with the animate function through some shared state (e.g. the state of the window manager).
Rather than solving the problem indirectly, let’s just stop the rocket from going past the bottom of the scene in land-rocket/v3.
How do we know when to stop the rocket? The fun answer is to try to stop the animation right when it hits the bottom, but its correctness depends on our reflexes. Reviewing our examples for land-rocket/v2, the rocket is flush at the bottom when n is 200. This makes sense, since the scene height is 200px and the rocket moves exactly the length of the scene.
We only want to place the rocket as we did in land-rocket/v2 while n is less than or equal to 200, otherwise we place the rocket at the same location as 200.
We can produce different outputs conditionally with a cond expression.
> (check-expect (cond [(number? "foo") "a number?"] [(string? "foo") "a string!"] [(= (+ 1 1) 2) "1+1=2"]) "a string!")
Each clause in a cond has two parts wrapped in square brackets: the question expression on the left and the result expression on the right. If any of the questions return #true, the corresponding result is returned.
The last clause may use else as a question that always succeeds.
> (check-expect (cond [(string? 42) "a string?"] [else "not a string!"]) "not a string!")
If no test succeeds, cond results in an error.
> (check-error (cond [#false "neither this one,"] [(= 1 2) "nor this one"]) "cond: all question results were false")
We can implement land-rocket/v3 using cond to stop moving the rocket when n is larger than 200.
; land-rocket/v3 : Natural -> Image ; Draw a rocket on an empty scene with the adjusted y-offset N. (define (land-rocket/v3 n) (cond [(<= n 200) (place-image RKT 50 (- n 36) (empty-scene 100 200))] [(> n 200) (place-image RKT 50 (- 200 36) (empty-scene 100 200))])) (land-rocket/v3 0) (land-rocket/v3 100) (land-rocket/v3 200) (land-rocket/v3 300)
Our last test shows the rocket still on the ground. We can confirm this by running the animation.
> (animate land-rocket/v3)
This is pretty cool, but I’m not happy with our rocket anymore. (Not nearly exciting enough.) Instead, let’s land a UFO!
Landing a UFO
(define UFO (overlay/xy (ellipse 30 22 'solid 'black) -26 5 (overlay (ellipse 72 22 'solid 'gray) (ellipse 76 26 'solid 'green) (ellipse 80 30 'solid 'black))))
We can implement land-ufo by replacing all uses of RKT in land-rocket/v3 with UFO, right?
; land-ufo : Natural -> Image ; Draw a ufo on an empty scene with the adjusted y-offset N. (define (land-ufo n) (cond [(<= n 200) (place-image UFO 50 (- n 36) (empty-scene 100 200))] [(> n 200) (place-image UFO 50 (- 200 36) (empty-scene 100 200))])) (land-ufo 0) (land-ufo 100) (land-ufo 200) (land-ufo 300)
Hmm, the UFO doesn’t quite make it to the bottom of the scene. The adjustment we used for RKT doesn’t work for UFO. So that adjustment do we need?
Recall why we made an adjustment in the first place. Our original land-rocket placed the rocket with the bottom 36px on the scene.
> (land-rocket 0)
What happens if we move it another 36px?
> (land-rocket 36)
It looks like it’s entirely on the scene. Judging this by eye got us in trouble earlier, but we can check this manually with the function image-height.
> (check-expect (image-height RKT) 72)
So, place-image measures its X/Y offsets from the center of RKT to the upper-left corner of the scene (and the documentation confirms this).
We can correct the adjustment in land-ufo/v2, using image-height to calculate the proper adjustment.
; land-ufo/v2 : Natural -> Image ; Draw a ufo on an empty scene with the adjusted y-offset N. (define (land-ufo/v2 n) (cond [(<= n 200) (place-image UFO 50 (- n (/ (image-height UFO) 2)) (empty-scene 100 200))] [(> n 200) (place-image UFO 50 (- 200 (/ (image-height UFO) 2)) (empty-scene 100 200))])) (land-ufo/v2 0) (land-ufo/v2 100) (land-ufo/v2 200) (land-ufo/v2 300)
No More Magic
The UFO lands exactly as expected! The constant 36 that we subtracted from the given natural number is known as a magic constant. We found it by trial and error, ignoring the reason why that particular adjustment was correct. Once we changed the conditions that made 36 the correct adjustment (by using an image with a different height) the magic went away.
Instead of blindly adjusting by 36 pixels, land-ufo/v2 moves the image up by half its height.
Are there any other magic constants in land-ufo/v2?
Answer 1: What about the 2 in each division that replaced 36?
Response 1: Not quite, place-image always measures from the center of the first image, so the 2 should only change if we stop using place-image, in which case we’d have to change all the arguments anyway.
A2: What about 50, the X offset given to place-image?
R2: Yes, we used 50 because it placed the image in the center of the scene. If we changed the width of the scene from 100, we would have to adjust the X offset as well.
A3: Isn’t the 200 in each of the cond questions is based on the height of the scene?
R3: Yep, those values are tied together too.
We can explicitly link these values together by naming the scene dimensions and referencing those constants inside land-ufo/v3.
; land-ufo/v3 : Natural -> Image ; Draw a ufo on an empty scene with ; its bottom N pixels from the top. ; Constants: (define W 100) (define H 200) ; (define (land-ufo/v3 n) (cond [(<= n H) (place-image UFO (/ W 2) (- n (/ (image-height UFO) 2)) (empty-scene W H))] [(> n H) (place-image UFO (/ W 2) (- H (/ (image-height UFO) 2)) (empty-scene W H))])) (land-ufo/v3 0) (land-ufo/v3 100) (land-ufo/v3 200) (land-ufo/v3 300)
Generalization
Q: Could we pass the scene width and height in as arguments to the function instead of referencing those constants?
A: We can, let’s do that instead, but we may run into another issue down the road.
Inside land-ufo/v3, we refer to the constants W and H that were defined outside the function. As suggested, we can instead generalize our function over the scene dimensions by adding them as arguments. This way we can draw the UFO on a scene of any size, as shown in land-ufo-on-scene.
; land-ufo-on-scene : Natural Natural Natural -> Image ; Draw a ufo on an empty scene of size WxH ; with its bottom N pixels from the top. (define (land-ufo-on-scene n w h) (cond [(<= n h) (place-image UFO (/ w 2) (- n (/ (image-height UFO) 2)) (empty-scene w h))] [(> n h) (place-image UFO (/ w 2) (- h (/ (image-height UFO) 2)) (empty-scene w h))])) (land-ufo-on-scene 0 100 200) (land-ufo-on-scene 100 120 80) (land-ufo-on-scene 200 80 120) (land-ufo-on-scene 300 100 500)
Since land-ufo-on-scene takes three arguments rather than one, it breaks animate’s contract and would cause an error. But we can define size-specific helpers in terms of land-ufo-on-scene that can be used with animate.
(define (land-ufo/100x200 n) (land-ufo-on-scene n 100 200)) (define (land-ufo/200x400 n) (land-ufo-on-scene n 200 400)) (define (land-ufo/80x40 n) (land-ufo-on-scene n 80 40)) (animate land-ufo/100x200) (animate land-ufo/200x400) (animate land-ufo/80x40)
We can even take one more step to generalize over the image as well, shown in land-image-on-scene. As before, we can define specialized helpers that can be passed to animate.
; land-image-on-scene : Natural Natural Natural -> Image ; Draw IMG on an empty scene of size WxH ; with its bottom N pixels from the top. (define (land-image-on-scene img n w h) (cond [(<= n h) (place-image img (/ w 2) (- n (/ (image-height img) 2)) (empty-scene w h))] [(> n h) (place-image img (/ w 2) (- h (/ (image-height img) 2)) (empty-scene w h))])) (define (land-rkt/100x200 n) (land-image-on-scene RKT n 100 200)) (define (land-ufo/80x80 n) (land-image-on-scene UFO n 80 80)) (land-rkt/100x200 0) (land-rkt/100x200 100) (land-rkt/100x200 200) (land-rkt/100x200 300) (land-ufo/80x80 0) (land-ufo/80x80 100) (land-ufo/80x80 200) (land-ufo/80x80 300) (animate land-rkt/100x200) (animate land-ufo/80x80)
Q: Can’t we use min to get rid of the cond?
A: That’s clever, and correct!
; land-image-on-scene/min : Natural Natural Natural -> Image ; Draw IMG on an empty scene of size WxH with its ; bottom N pixels from the top (without a cond). (define (land-image-on-scene/min img n w h) (place-image img (/ w 2) (- (min n h) (/ (image-height img) 2)) (empty-scene w h))) (define (land-rkt/min n) (land-image-on-scene RKT n 100 200)) (land-rkt/min 0) (land-rkt/min 100) (land-rkt/min 200) (land-rkt/min 300) (animate land-rkt/min)
But, should we? To me, it’s less obvious that land-image-on-scene/min has different behavior when the arguments N and H satisfy certain conditions (relative to land-image-on-scene). While the use of min makes the function smaller and removes repeated expressions, it may not make the function easier to understand. With all else equal, the better implementation is the one that is easiest to understand. Anyone looking at your code years down the line will thank you.
5 September 8, 2017
Audio and video capture from today’s class is available here.
6 September 11, 2017
Audio and video capture from today’s class is available here.
Code from today’s lecture:
7 September 13, 2017
Audio and video capture from today’s class is available here.
Code from today’s lecture:
8 September 15, 2017
Audio and video capture from today’s class is available here.
Code from today’s lecture (remember, it has failing test cases):
Today’s quiz:
A Coord is a (make-posn Integer Integer). Interp: a point on the Cartesian plane.
Write a function dist : Coord -> Number that computes the distance from the origin.
Recall: distance of (x,y) to (0,0) is √(x²+y²).
You do not need to perform all steps of the DR, just define the function.
9 September 18, 2017
Audio and video capture from today’s class is available here.
We didn’t really write any code; we discussed templates, stubs, the three kinds of errors, and failing test cases.
Today’s quizzes were (1) exactly the quiz from Friday and (2):
A Lec is one of: |
- "M" |
- "W" |
- "F" |
Interp: day of the week for 131A lecture |
|
Write a template for a Lec function. |
Here are some common issues encountered so far in grading Assignment 3: Designing and composing functions:
Most students place test cases below their def’n instead of between signature and def’n.
Some people included function examples in comments without writing concrete test cases. Some had both.
Almost every submission had some incorrect indentation and long lines.
The format-month almost universally lacked helper usage and contained long lines.
- Some students defined "helpers" that didn’t "help" at all, basically like:
(define (supposed-to-implement x)
(so-called-helper x))
Many submissions had stubs still left in their code either as a comment or as a defined function like (define (format-month-stub ...) "Nov").
There were lots of submissions with just templates defined for every function, or data templates that were just wrong.
General disorganization was common, e.g. signatures and test cases thrown about randomly and not coupled together with the function def’n. Some people renamed the functions to something else which made it difficult to grade.
Lots of long function bodies were defined on the same line as the "define".
Commonly init-time was defined as a function instead of just as an expression in terms of init-* constants.
A surprising amount of submission weren’t even grammatically well-formed BSL programs. :(
Make sure you correct any of these issues if they occur in your program for Assignment 4: Style and design.
10 September 20, 2017
Audio and video capture from today’s class is available here.
Here is the code for simple space invaders designed using the design recipe and adhering to The Style:
I’ve made a two part video that develops the invader program from scratch, resulting in the code above. You can watch this to get a complete example of following the DR through on an involved example.
11 September 22, 2017
Audio and video capture from today’s class is available here.
12 Midterm 1 Drills
Here are some drill questions to practice for the first midterm. These only cover topics we’ve covered so far in class, but more topics will be on the midterm. I will post relevant drill problems as appropriate.
12.1 Simple computations
Determine what the following programs evaluate to:
(- (sqr 5))
(modulo 12 5)
(+ (/ 4 3) 1)
(string-append "Hello" "World")
(string-append "" "Fred")
(substring "manslaughter" 4)
(above (circle 10 "outline" "black") (square 5 "outline" "black"))
(substring (string-append "te" "am") 1 3)
(+ (posn-x (make-posn 3 4)) (posn-x (make-posn 10 2)))
(define-struct name (first last)) (make-name "James" "Bond") (define first-name "James") (define last-name "Bond") (string-append last-name ", " first-name " " last-name) (define x 3) (define y 4) (sqrt (+ (sqr x) (sqr y))) (define-struct name (first last)) (define ms (make-name "Michael" "Scott")) (define sm (make-name (name-last ms) (name-first ms))) (name-last sm) (define (f x) (/ (sqr x) 2)) (+ (f 5) (f 2)) (define (g y) (cond [(<= (string-length y) 4) 3.25] [else "yellow"])) (g "pie")
12.2 Stepping through computations
Write out each step of computation. At each step, underline the expression being simplified. Label each step as being "arithmetic" (meaning any built-in operation), "conditional", "plug" (for plugging in an argument for a function parameter), or "constant" for replacing a constant with its value.
(+ (sqr 5) (add1 2))
(define Q 2) (define (h z) (+ (* z 5) Q)) (cond [(= (h 1) 7) (add1 9)] [(= (h 2) 12) 4]) (define (hi name) (string-append "Hi " name "!")) (hi (substring "DVH" 0 1)) (define s (make-posn "GOOG" 99)) (cond [(< 100 (posn-y s)) "sell"] [(> 100 (posn-y s)) "buy"] [else "nada"])
12.3 Classifying errors
Classify the following programs as having a syntax error, a run-time error, logical error, or having no errors.
(define (f x) (expt 2 x)) (check-expect (f 4)) (string-append "Hi " (substring "DVH" 1 4))
; dist : Number Number -> Number ; Compute distance to origin of (x,y) (define (dist x y) (sqrt (+ (sqr x) (sqr x)))) (dist 3 4) (define h z (+ z (sqr z)))
12.4 Stubs, Templates
Assume the following data definitions:
; A Name is a (make-name String String) (define-struct name (first last)) ; A Shape is one of: ; - (make-rect Integer Integer) ; - (make-circ Integer) (define-struct rect (width height)) (define-struct circ (radius)) ; A Drawing is one of: ; - Shape ; - (make-posn Shape Shape) ; A Price is one of ; - [0,99) ; - [99,999) ; A Move is one: ; - "N" ; - "E" ; - "W" ; - "S" ; - "NE" ; - "NW" ; - "SE" ; - "SW" ; A MaybeMove is one of: ; - Move ; - #false ; A Niner is a 9 ; A Biz is one of: ; - "a" ; - 7 ; - #true ; - (make-posn 9 9)
Write templates for each of these data definitions.
Write stubs for each of these signatures.
; greeting : Name -> String ; cheap? : Price -> Boolean ; next-move : Move -> MaybeMove ; area : Drawing -> Number ; sign : Shape -> Name ; inc : Number -> Niner ; choose : Move Move -> Move ; cost : Drawing -> Price ; cap : Shape String Image -> Biz ; same-price? : Price Price -> Boolean ; bribe : Price -> Name ; change-last : Name String -> Name ; dot : String Integer -> String ; cross : String Move -> Shape ; all-on? : Shape Shape Shape Shape -> Boolean ; flip : Move -> Move ; rotate : Image MaybeMove -> Shape
12.5 Designing functions
; A Name is a (make-name String String) ; Interp: a person's full (first and last) name. ; Both strings must contain at least one letter. (define-struct name (first last))
Design a function that creates a opening phrase of a letter. For example, given the full name David Van Horn, produces "Dear David,".
Design a function that is given two full names and a first name. It should produce a new name using the given first name and a hyphenated combination of the last names of the two full names. For example, given full names Ed Tobin, Laura Hochstadt, and the first name Sam, it should produce the full name Sam Tobin-Hochstadt.
Design a function that is given a full name and produces a “private” version of the name that abbreviates the last name to the first letter and a period. So for example, given the full name David Van Horn, then the full name David V. would be the produced.
Design a function that is given two full names and determines whether the two people have the same first name.
; A Dir is one of: ; - "N" ; - "E" ; - "W" ; - "S" ; Interp: North, East, West, and South.
Design a function that computes the opposite of a given direction.
Design a function that determines if two directions are the same.
Design a function that determines if two directions are opposites of each other.
Design a function that computes a right turn from the given direction.
Design a function that given a direction computes a name (as in a Name) like this: given "S" it should compute "South Southwest" where South is the first name and Southwest is the last name. North should give you North Northwest, etc.
; A Coord is a (make-posn Integer Integer) ; Interp: a Cartesian coordinate
Design a function that takes two coordinates and computes a coordinate representing their sum, e.g. (x1,y1) + (x2,y2) = (x1+x2,y1+y2).
Design a function that, given a coordinate (x,y), computes the area of the triangle formed by (0,0), (x,0), and (x,y). Recall the area of a triangle is 1/2 * base * height.
Design a function that, given a coordinate (x,y), computes the perimeter of the triangle formed by (0,0), (x,0), (x,y).
Design a function that reflects a coordinate over the x-axis, e.g. (5,3) becomes (5,-3).
12.6 Solutions
Here are videos going through solutions to each part of the drill problems:
Designing Dir functions : the video file was corrupted
13 September 25, 2017
Audio and video capture from today’s class is available here.
Here are the comments I made in regard to what we’ve seen so far in assignment 4 submissions: feedback-assign4.pdf.
Here is the code for today (I re-arranged it slightly to follow the style guidelines):
14 Midterm practice exam
15 September 27, 2017
Audio and video capture from today’s class is available here.
Here is the code for today; we skipped the section on lists of strings, so see if you can do that on your own and also have a go at the functions on lists of lists of numbers we didn’t get to.
Today’s quiz:
;; An Onion is one of: |
;; - (make-bulb) |
;; - (make-skin Onion) |
(define-struct bulb ()) |
(define-struct skin (inner)) |
Write a template for Onion functions.
16 September 29, 2017
Audio and video capture from today’s class is available here.
Today’s quiz:
;; An Onion is one of: |
;; - (make-bulb) |
;; - (make-skin Onion) |
(define-struct bulb ()) |
(define-struct skin (inner)) |
Write the definition of the count-skins function:
(define b (make-bulb)) |
|
;; count-skins : Onion -> Natural |
;; Count the number of skins on the onion |
(check-expect (count-skins b) 0) |
(check-expect (count-skins (make-skin b)) 1) |
(check-expect (count-skins (make-skin (make-skin b))) 2) |
17 Pair programming Space Invaders with shots
(a) how the head and hands model of pair programming can be effective in rapidly thinking through and solving problems and
(b) how sticking to the design process makes short order of the assignment.
We were able to complete that part of the assignment in 1 hour. As
you watch the video, I hope you’ll realize we were able to get through
it so quickly not because we are overly smart, experienced, or have an
encyclopedic knowledge of BSL or Space Invaders—
I made only one change to the code after we finished, which is I deleted all the obsoleted code having to do with Aim and Fire.
18 October 4, 2017
Audio and video capture from today’s class is available here.
Today’s code:
19 October 6 & 9, 2017
The Snake Game
What things change over time in the snake game?
Per the discussion in the previous lecture:
the length of the snake
the placement of the food
the x, y of the head of the snake
the score
when the snake turns
position of each segment of the snake’s body
if the snake is eating food or not
when the food is produced
when you lose
For each of the changes that were listed out on Wednesday, which information can be computed based on other values and which are necessary to remember?
Things that Change
Many of the listed "things that change" do not have to be directly represented.
✗ The length of the snake can be computed;
✓ the placement of the food must be remembered;
✗ the x, y of the head of the snake is no different from other segments;
✗ the score will be computed as the length of the snake;
✓ when the snake turns or rather, the direction the snake is moving;
✓ position of each segment of the snake’s body must be remembered;
✗ if the snake is eating food or not is known based on the location of the snake’s head and the locations of the food;
✗ when the food is produced will occur with some constant probability; and
✗ when you lose is known based on the location of the snake’s segments and the game borders.
So, what’s left?
the X, Y of all food must be known,
the direction in which the snake moves must be known, and
the X, Y of every segment of the snake must be known.
The only thing that distinguishes one block of food from another is its location, so, let’s implement Food as Posns.
; A Food is a (make-posn Int Int) ; Interp: the location of a block of food in the game. ; food-template : Food -> ??? (define (food-template f) (... (posn-x f) ... (posn-y f) ...))
There can be an arbitrary amount of food on the game board, so...
; A ListofFood is one of: ; - '() ; - (cons Food ListofFood) ; Interp: an arbitrary amount of Food. ; foods-template : ListofFood -> ??? (define (foods-template fs) (cond [(empty? fs) ...] [(cons? fs) (... (first fs) ... (foods-template (rest fs)))]))
force you to understand the data you’re using in your implementation and
make writing tests for your functions much faster.
The Snake can move in one of four directions, so we use four strings to distinguish these directions.
; A Dir is one of: "left", "right", "up", or "down". ; Interp: the direction in which the head of the snake is moving. ; dir-template : Dir -> ??? (define (dir-template d) (cond [(string=? "left" d) ...] [(string=? "right" d) ...] [(string=? "up" d) ...] [(string=? "down" d) ...]))
We could use any four distinct values for this purpose, such as one of four numbers {1, 2, 3, 4}, or one of four distinct Posns {(make-posn 0 1), (make-posn 1 0), (make-posn -1 0), (make-posn 0 -1)}). Think a bit about why are some choices better than others.
With the choice below, not only is the direction obvious at a glance, but each Dir happens to be a valid KeyEvent. This may end up being useful as we design the rest of the program.
Each segment of the snake has a location, so let’s use Posns again to represent each Seg in the snake.
; A Seg is (make-posn Int Int) ; Interp: the location of one piece of the snake ; seg-template : Seg -> ??? (define (seg-template s) (... (posn-x s) ... (posn-y s) ...))
A snake may be arbitrarily long, so we’ll need some way to represent an arbitrary number of segments. But what’s the smallest number of Segs that constitute a snake? It must start with at least one, so we need a data definition that contains one or more Segs. Per the definition below, it’s impossible to create a NEListofSeg with no Segs in it.
; A NEListofSeg is one of: ; - (cons Seg '()) ; - (cons Seg NEListofSeg) ; Interp: the segments of the snake in the game, where the first is the snake's ; head.
This is different than other lists we’ve seen, since all other lists allowed a list of zero-length. When writing our template for any functions that operate on NEListofSegs, we’ll need to distinguish these two cases using something other than empty?. How is the first case in the NEListofSeg data definition different from the second? Its rest is '()!
; segs-template : NEListofSeg -> ??? (define (segs-template ss) (cond [(empty? (rest ss)) (... (first ss) ...)] [(cons? (rest ss)) (... (first ss) ... (segs-template (rest ss)))]))
Now we can give a data definition for a Snake:
; A Snake is a (make-snake NEListofSeg Dir) ; Interp: All of the segments inside the snake and the direction ; that the snake is moving. (define-struct snake (segs dir)) ; snake-template : Snake -> ??? (define (snake-template s) (... (segs-template (snake-segs s)) ... (dir-template (snake-dir s)) ...))
This is everything we need in the WorldState of our Game:
; A Game is a (make-game Snake ListofFood) ; Interp: the WorldState of the snake game. (define-struct game (snake foods))
As with all composite data, given a Game we can tear it apart. Each of Snake and ListofFood have their own templates. Explicitly applying those templates will give hints for where we should expect to need helper-functions when working with Games.
; game-template : Game -> ??? (define (game-template g) (... (snake-template (game-snake g)) ... (foods-template (game-foods g)) ...))
Blocks help us scale the game board to any size we want and simplify other operations. The Snake moves a single Block each tick. Each of the Segs and Food are a single Block. Each block is rendered as a square BLOCK-SCALE pixels wide.
; A Block is a (make-posn Int Int) ; Interp: the smallest unit of measure on the game board.
With these data definitions, we can implement the operations for our snake game.
Aside: defining examples
Every single student I interact with during office hours does not test their functions. The core reason is that writing tests for the function is the hardest part of function design. There is a reason why writing tests is hard.
how to construct valid input values,
how to construct a valid output value, and
how the input values are used to create the output value
If you’ve actually followed the design recipe when you were creating your data definitions, you’ve already created a bunch of valid input values for any function that operates those data definitions. This lets you focus on the important part of the test: the expected output, and particularly, how the input is used to create the expected output.
Here are some simple examples of Games, which requires examples of each data definition we’ve created.
(define DIR0 "down") (define DIR1 "right") (define DIR2 "up") (define SEG0 (make-posn 0 0)) (define SEG1 (make-posn 0 1)) (define SEG2 (make-posn 1 1)) (define SEGS0 (list SEG0)) (define SEGS1 (cons SEG1 SEGS0)) (define SEGS2 (cons SEG2 SEGS1)) (define SNAKE0 (make-snake SEGS0 DIR0)) (define SNAKE1 (make-snake SEGS1 DIR1)) (define SNAKE2 (make-snake SEGS2 DIR2)) (define FOOD0 (make-posn 1 1)) (define FOOD1 (make-posn 2 2)) (define FOOD2 (make-posn 3 2)) (define FOODS0 '()) (define FOODS1 (cons FOOD0 FOODS0)) (define FOODS2 (cons FOOD1 FOODS1)) (define FOODS3 (cons FOOD2 FOODS2)) (define GAME0 (make-game SNAKE0 FOODS0)) ; eating on next turn: (define GAME1 (make-game SNAKE1 FOODS1)) (define GAME2 (make-game SNAKE2 FOODS2)) ; collision with self: (define GAMEOVER0 (make-game (make-snake (list* (make-posn 0 0) (make-posn 1 0) SEGS2) "left") FOODS3)) ; collision with wall: (define GAMEOVER1 (make-game (make-snake (cons (make-posn -1 0) SEGS0) "left") FOODS2))
Top-down design of the snake game
Where do we start? At the top! How? The same way as always, assume we’ve got functions that do exactly what we want, then design them.
We’ll use big-bang, so let’s start working out that main function to help us design the program as a whole. We have to give big-bang our initial Game as input. We’ll need a way to-draw each Game. Things that change over time occur on-tick: including snake movement, snake growth, and food generation. The snake’s direction changes on-key events. The Game should stop-when the snake collides with itself or the edges of the scene.
; main : Game -> Game ; Run the snake game using ‘big-bang' given the initial world state. (define (main g) (big-bang g ; (Game) [to-draw draw-game] ; (Game -> Image) [on-tick tock-game 1/4] ; (Game -> Game) [on-key keyh-game] ; (Game KeyEvent -> Game) [stop-when stop-game ; (Game -> Boolean) game-over])) ; (Game -> Image)
We know what the signatures of these functions must be from the documentation of big-bang. So, let’s implement them!
Drawing the Game
Blocks make drawing the game quite easy. We draw each Block as a square BLOCK-SCALE pixels wide, so the only function that actually deals with pixel values is draw-block-on.
Note: Our drawing functions always take as input the scene on which new images should be placed.
(define BLOCK-SCALE 10) ; Block -> Pixel scale (define MTW 40) ; Game board width (# blocks) (define MTH 30) ; Game board height (# blocks) (define MT (rectangle (* (+ 1 MTW) BLOCK-SCALE) (* (+ 1 MTH) BLOCK-SCALE) "solid" "black")) ; draw-block-on : Block Color Image -> Image ; Places a square of color C at the scaled pixel ; location denoted by B on SCN. (define (draw-block-on b c scn) (place-image (square BLOCK-SCALE "solid" c) (* (+ 1 (posn-x b)) BLOCK-SCALE) (* (+ 1 (posn-y b)) BLOCk-SCALE) scn)) ; draw-block-on : LoBlock Color Image -> Image ; Places a square of color C at the scaled pixel ; location denoted by B on SCN. (define (draw-blocks-on bs c scn) (cond [(empty? bs) scn] [(cons? bs) (draw-blocks-on (rest bs) c (draw-block-on (first bs) c scn))])) (define SEGCOLOR "yellow") (define FOODCOLOR "red") ; draw-game : Game -> Image ; Render the snake game as an image. (define (draw-game g) (draw-blocks-on (snake-segs (game-snake g)) SEGCOLOR (draw-blocks-on (game-foods g) FOODCOLOR MT))) (define GAMEOVER-SIZE 32) (define GAMEOVER-COLOR "red") (define GAMEOVER-MSG "Final score: ") ; game-score : Game -> Natural ; Calculate the score of the game as the number of snake segments. (define (game-score g) (length (snake-segs (game-snake g)))) (check-expect (game-score GAME0) 1) (check-expect (game-score GAME1) 2) (check-expect (game-score GAME2) 3) ; game-over : Game -> Image ; Display the score once we stop the world. (define (game-over g) (overlay (text (string-append GAMEOVER-MSG (number->string (game-score g))) GAMEOVER-SIZE GAMEOVER-COLOR) (draw-game g))) (check-expect (game-over GAME0) (overlay (text (string-append GAMEOVER-MSG "1") GAMEOVER-SIZE GAMEOVER-COLOR) (draw-game GAME0))) (check-expect (game-over GAME1) (overlay (text (string-append GAMEOVER-MSG "2") GAMEOVER-SIZE GAMEOVER-COLOR) (draw-game GAME1))) (check-expect (game-over GAME2) (overlay (text (string-append GAMEOVER-MSG "3") GAMEOVER-SIZE GAMEOVER-COLOR) (draw-game GAME2)))
Ticking the Game
The snake grows if it’s eating or
moves if it isn’t, and
food appears randomly at the snake’s tail (~20% of the time).
The snake is eating if in the next game state, its head Seg is overlapping with some Food on the game board. Assuming that next-head gives us the next head Seg of the snake, we’ve can implement eating?:
; eating? : Snake ListofFood -> Boolean ; Is the snake eating food in the next state? (define (eating? s fs) (member? (next-head s) fs)) (check-expect (eating? SNAKE0 FOODS0) #false) (check-expect (eating? SNAKE1 FOODS1) #true) (check-expect (eating? SNAKE2 FOODS2) #false)
So, we need to design next-head as well. We’ve already decided that the next head will be one Block away from the current-head. The current head of the snake is easy:
; current-head : Snake -> Seg ; Return the head segment of the given snake. (define (current-head s) (first (snake-segs s))) (check-expect (current-head SNAKE0) SEG0) (check-expect (current-head SNAKE1) SEG1) (check-expect (current-head SNAKE2) SEG2)
So, we just need to know in which Dir that one Block should be added to implement next-head:
; next-head : Snake -> Seg ; Return the next head segment of the given snake. (define (next-head s) (cond [(string=? "left" (snake-dir s)) (make-posn (- (posn-x (current-head s)) 1) (posn-y (current-head s)))] [(string=? "right" (snake-dir s)) (make-posn (+ 1 (posn-x (current-head s))) (posn-y (current-head s)))] [(string=? "down" (snake-dir s)) (make-posn (posn-x (current-head s)) (+ 1 (posn-y (current-head s))))] [(string=? "up" (snake-dir s)) (make-posn (posn-x (current-head s)) (- (posn-y (current-head s)) 1))])) (check-expect (next-head SNAKE0) (make-posn (posn-x (current-head SNAKE0)) (+ 1 (posn-y (current-head SNAKE0))))) (check-expect (next-head SNAKE1) (make-posn (+ 1 (posn-x (current-head SNAKE1))) (posn-y (current-head SNAKE1)))) (check-expect (next-head SNAKE2) (make-posn (posn-x (current-head SNAKE2)) (- (posn-y (current-head SNAKE2)) 1)))
Now we know how to test if the snake is eating? on the next tick. On each tick the snake’s next-head will be added to the snake’s ListofSeg. If the snake is not eating? its last Seg is removed; if the snake is eating? it is not.
The function next-snake implements this behavior with the help of move-snake and grow-snake, and remove-last.
Note the signature remove-last : NEListofSeg -> ListofSeg. If remove-last is given a single-element list it will return the empty list, so it would be incorrect to give NEListofSeg as the return type. But once we add the next-head to the ListofSeg, we once again know we’re satisfying make-snake’s signature.
; next-snake : Snake ListofFood -> Snake ; Create the next snake given the last snake and the existing food. (define (next-snake s fs) (cond [(eating? s fs) (grow-snake s)] [else (move-snake s)])) (check-expect (next-snake SNAKE0 FOODS0) (make-snake (list SEG1) DIR0)) (check-expect (next-snake SNAKE1 FOODS1) (make-snake SEGS2 DIR1)) (check-expect (next-snake SNAKE2 FOODS2) (make-snake (list (make-posn 1 0) (make-posn 1 1) (make-posn 0 1)) DIR2)) ; move-snake : Snake -> Snake ; Creates a new snake with the next head and the last segment removed. (define (move-snake s) (make-snake (cons (next-head s) (remove-last (snake-segs s))) (snake-dir s))) (check-expect (move-snake SNAKE0) (make-snake (list SEG1) DIR0)) (check-expect (move-snake SNAKE1) (make-snake (list SEG2 SEG1) DIR1)) (check-expect (move-snake SNAKE2) (make-snake (list (make-posn 1 0) (make-posn 1 1) (make-posn 0 1)) DIR2)) ; grow-snake : Snake -> Snake ; Creates a new snake with the next head added. (define (grow-snake s) (make-snake (cons (next-head s) (snake-segs s)) (snake-dir s))) (check-expect (grow-snake SNAKE0) (make-snake SEGS1 DIR0)) (check-expect (grow-snake SNAKE1) (make-snake SEGS2 DIR1)) (check-expect (grow-snake SNAKE2) (make-snake (cons (make-posn 1 0) SEGS2) DIR2)) ; remove-last : NELoSeg -> LoSeg ; Removes the last element from the given NELoSeg. ; Note: the returned list may not be non-empty. (define (remove-last ss) (cond [(empty? (rest ss)) '()] [else (cons (first ss) (remove-last (rest ss)))])) (check-expect (remove-last SEGS0) '()) (check-expect (remove-last SEGS1) (list (make-posn 0 1))) (check-expect (remove-last SEGS2) (list (make-posn 1 1) (make-posn 0 1)))
Finally, we have to handle Food generation. We’ve decided to generate food about once every 5 moves of the snake, and we’ll define a value to easily configure that parameter. If we add food, we’ll add it on the tail of the snake.
; maybe-add-food : Snake ListofFood -> ListofFood ; Add food under the tail of the snake about FOOD-FREQ⁻¹ often. (define FOOD-FREQ 5) (define (maybe-add-food s fs) (cond [(= 0 (random FOOD-FREQ)) (cons (return-last (snake-segs s)) fs)] [else fs])) (check-random (maybe-add-food SNAKE0 FOODS0) (cond [(= 0 (random FOOD-FREQ)) (cons SEG0 FOODS0)] [else FOODS0])) (check-random (maybe-add-food SNAKE1 FOODS1) (cond [(= 0 (random FOOD-FREQ)) (cons SEG0 FOODS1)] [else FOODS1])) (check-random (maybe-add-food SNAKE2 FOODS2) (cond [(= 0 (random FOOD-FREQ)) (cons SEG0 FOODS2)] [else FOODS2])) ; return-last : NELoSeg -> Seg ; Returns the last element. (define (return-last ss) (cond [(empty? (rest ss)) (first ss)] [else (return-last (rest ss))])) (check-expect (return-last SEGS0) SEG0) (check-expect (return-last SEGS1) SEG0) (check-expect (return-last (reverse SEGS2)) SEG2) ; next-foods : Snake ListofFood -> ListofFood (define (next-foods s fs) (maybe-add-food s (remove (next-head s) fs))) (check-random (next-foods SNAKE0 FOODS0) (maybe-add-food SNAKE0 (remove (next-head SNAKE0) FOODS0))) (check-random (next-foods SNAKE1 FOODS1) (maybe-add-food SNAKE1 (remove (next-head SNAKE1) FOODS1))) (check-random (next-foods SNAKE2 FOODS2) (maybe-add-food SNAKE2 (remove (next-head SNAKE2) FOODS2)))
This was the last piece we need to add to implement tock-game.
; tock-game : Game -> Game ; Change the state of the snake game after one clock tick. (define (tock-game g) (make-game (next-snake (game-snake g) (game-foods g)) (next-foods (game-snake g) (game-foods g)))) (check-random (tock-game GAME0) ; not eating (make-game (move-snake SNAKE0) (maybe-add-food SNAKE0 FOODS0))) (check-random (tock-game GAME1) ; eating (make-game (grow-snake SNAKE1) (maybe-add-food SNAKE1 (remove (next-head SNAKE1) FOODS1)))) (check-random (tock-game GAME2) ; not eating (make-game (move-snake SNAKE2) (maybe-add-food SNAKE2 FOODS2)))
Stopping the Game
The snake game ends when the snake collides with itself or if it goes off the game board.
; on-board? : Seg -> Boolean ; Returns true only if the given segment is on the game board. (define (on-board? s) (and (>= (posn-x s) 0) (>= (posn-y s) 0) (<= (posn-x s) MTW) (<= (posn-y s) MTH))) (check-expect (on-board? SEG0) #true) (check-expect (on-board? SEG1) #true) (check-expect (on-board? SEG2) #true) (check-expect (on-board? (make-posn -1 0)) #false) (check-expect (on-board? (make-posn 0 -1)) #false) (check-expect (on-board? (make-posn (+ MTW 1) 0)) #false) (check-expect (on-board? (make-posn 0 (+ MTH 1))) #false) (check-expect (on-board? (make-posn -1 (+ MTH 1))) #false) ; stop-game : Game -> Boolean ; Stop the snake game when ; - the snake collides with the wall or ; - the snake collides with itself. (define (stop-game g) (or (member? (current-head (game-snake g)) (rest (snake-segs (game-snake g)))) (not (on-board? (current-head (game-snake g)))))) (check-expect (stop-game GAME0) #false) (check-expect (stop-game GAME1) #false) (check-expect (stop-game GAME2) #false) (check-expect (stop-game GAMEOVER0) #true) (check-expect (stop-game GAMEOVER1) #true)
Controlling the Game
We want the snake to move with the arrow keys. Per the documentation, the KeyEvents associated with the arrow keys are precisely Dirs. This makes the keyh-game quite easy to implement.
; keyh-game : Game KeyEvent -> Game ; Handle big-bang key events for the snake game. (define (keyh-game g ke) (cond [(or (string=? ke "left") (string=? ke "right") (string=? ke "down") (string=? ke "up")) (make-game (make-snake (snake-segs (game-snake g)) ke) (game-foods g))] [else g])) (check-expect (keyh-game GAME0 "right") (make-game (make-snake SEGS0 "right") FOODS0)) (check-expect (keyh-game GAME1 "left") (make-game (make-snake SEGS1 "left") FOODS1)) (check-expect (keyh-game GAME2 "down") (make-game (make-snake SEGS2 "down") FOODS2))
Now we can run our snake game by passing any example game to main.
20 October 11, 2017
Audio and video capture from today’s class is available here.
Today’s code:
21 October 13, 2017
Audio and video capture from today’s class is available here.
Today’s code:
22 October 16, 2017
Audio and video capture from today’s class is available here.
23 October 18, 2017
Audio and video capture from today’s class is available here.
Today’s code: using-abstractions.rkt
Today’s quiz:
; my-append : [X] [Listof X] [Listof X] -> [Listof X] ; Append the elements of ls1 and ls2 (check-expect (my-append '() '()) '()) (check-expect (my-append '() (list 4 5 6)) (list 4 5 6)) (check-expect (my-append (list 1 2 3) '()) (list 1 2 3)) (check-expect (my-append (list 1 2 3) (list 4 5 6)) (list 1 2 3 4 5 6)) (define (my-append ls1 ls2) (cond [(empty? ls1) ls2] [(cons? ls1) (cons (first ls1) (my-append (rest ls1) ls2))])) ; Quiz: Give an equivalent definition of my-append ; in terms of foldr ; Recall: ; foldr : [X Y] (X Y -> Y) Y [Listof X] -> Y
24 Midterm 1 solution videos
Here is a series of videos going through the exam and constructing answers:
25 October 20, 2017
Audio and video capture from today’s class is available here.
The code will not be posted for this lecture (but can be seen in the video).
The first quiz from today:
; flatten : [X] [Listof [Listof X]] -> [Listof X] ; Flatten a list of lists of elements into a list of elements (check-expect (flatten '()) '()) (check-expect (flatten (list (list 1 2 3)) (list 4 5) (list 6)) (list 1 2 3 4 5 6)) (define (flatten lolox) (cond [(empty? lolox) '()] [(cons? lolox) (append (first lolox) (flatten (rest lolox)))])) ; Quiz: Give an equivalent definition of flatten ; in terms of foldr ; Recall: ; foldr : [X Y] (X Y -> Y) Y [Listof X] -> Y
The second quiz:
; largest : [Listof Number] Number -> Number ; Determine the largest number among all elements of the list and given number (check-expect (largest '() 5) 5) (check-expect (largest (list 1 2 3) 5) 5) (check-expect (largest (list 6 5 4) 5) 6) (define (largest lon n) (cond [(empty? lon) n] [(cons? lon) (max (first lon) (largest (rest lon) n))])) ; Quiz: Give an equivalent definition of largest ; in terms of foldr ; Recall: ; foldr : [X Y] (X Y -> Y) Y [Listof X] -> Y
26 October 23, 2017
Audio and video capture from today’s class is available here.
Again the code will not be posted, but can be seen in the video.
Today’s quiz:
; all-longer-than? : [Listof String] Number -> Boolean ; Are all of the strings longer than n characters long? (check-expect (all-longer-than? '() 1) #true) (check-expect (all-longer-than? (list "a" "b" "c") 1) #false) (check-expect (all-longer-than? (list "abc" "def") 1) #true) (define (all-longer-than? los n) (cond [(empty? los) #true] [(cons? los) (and (> (string-length (first los)) n) (all-longer-than? (rest los) n))])) ; Quiz: Give an equivalent definition of all-longer-than? ; in terms of andmap ; Recall: ; andmap : [X] (X -> Boolean) [Listof X] -> Boolean
27 October 25, 2017
Audio and video capture from today’s class is available here.
Today’s quiz:
; erma : ____________________________ (check-expect (erma (list sqr add1)) (list 25 6)) (check-expect (erma (list number->string)) (list "5")) (define (erma lof) (cond [(empty? lof) '()] [(cons? lof) (local [(define f (first lof))] (cons (f 5) (erma (rest lof))))])) ; QUIZ: Give a parametric signature for erma.
Today’s code: adventure.rkt.
28 October 27, 2017
Audio and video capture from today’s class is available here.
Today’s code: adventure2.rkt.
29 Midterm 2 practice
Here is the second midterm practice exam: m2-practice.pdf (m2-practice-soln.pdf).
30 October 30, 2017
Audio and video capture from today’s class is available here.
Today’s code: multi-inputs.rkt.
; wilma : ___________________________ (check-expect (wilma add1 5) (list 6 5 4 3 2 1)) (check-expect (wilma number->string 3) (list "3" "2" "1" "0")) (define (wilma f n) (cond [(zero? n) (list (f 0))] [else (cons (f n) (wilma f (sub1 n)))])) ; QUIZ: Give a parametric signature for wilma.
31 November 1, 2017
Audio and video capture from today’s class is available here.
Today’s code:
32 Midterm 2 Drills
Here are some drill problems. (Solutions: drill-soln.rkt.)
Keep in mind that any topic from midterm 1 could show up again on midterm 2 so it may be worth revisiting older drill problems and the practice midterm 1.
32.1 Programming with functions
Design and abstraction called andf from the following two functions:
; even-pos? : Number -> Boolean ; Is the number even and positive? (check-expect (even-pos? 4) #true) (check-expect (even-pos? 3) #false) (check-expect (even-pos? -1) #false) (define (even-pos? n) (and (even? n) (positive? n))) ; neg-odd? : Number -> Boolean ; Is the number negative and odd? (check-expect (neg-odd? 4) #false) (check-expect (neg-odd? 3) #false) (check-expect (neg-odd? -1) #true) (define (neg-odd? n) (and (negative? n) (odd? n)))
Be sure to give andf the most general parametric signature that is valid.
Use your abstraction to define the following function (you may find string-alphabetic? and string-lower-case? helpful):
; string-lower-alpha? : String -> Boolean ; Is the string made up of lower case, alphabetic letters? (check-expect (string-lower-alpha? "ABC") #false) (check-expect (string-lower-alpha? "a2c") #false) (check-expect (string-lower-alpha? "abc") #true) (define (string-lower-alpha? s) ...)
Using only andf, >, even?, and lambda expressions, write an expression that produces a predicate on numbers that will produce true when applied to even numbers greater than 5.
32.2 Signatures
Provide the most general valid signature for the following functions.
(define (lengths xs) (map length xs)) (define (total-length xs) (foldr (λ (x t) (+ (length x) t)) 0 xs)) (define (map-f-zero lof) (map (λ (f) (f 0)) lof))
32.3 Using list abstractions
Re-define the following functions in terms of list abstraction functions where appropriate. (Signatures and purpose statements intentionally omitted):
(check-expect (rev-append (list "there" "hi")) "hithere") (define (rev-append los) (cond [(empty? los) ""] [(cons? los) (string-append (rev-append (rest los)) (first los))])) (check-expect (posns-at-x (list 1 2 3) 7) (list (make-posn 7 1) (make-posn 7 2) (make-posn 7 3))) (define (posns-at-x ys x) (cond [(empty? ys) '()] [(cons? ys) (cons (make-posn x (first ys)) (posns-at-x (rest ys) x))])) (check-expect (dist (make-posn 0 0) (make-posn 3 4)) 5) (define (dist p q) (sqrt (+ (sqr (- (posn-x p) (posn-x q))) (sqr (- (posn-y p) (posn-y q)))))) (check-expect (close-by (make-posn 0 0) (list (make-posn 3 4) (make-posn 8 8)) 6) (list (make-posn 3 4))) (define (close-by p lop d) (cond [(empty? lop) '()] [(cons? lop) (cond [(<= (dist p (first lop)) d) (cons (first lop) (close-by p (rest lop) d))] [else (close-by p (rest lop) d)])])) (check-expect (draw-on (list (make-posn 50 50))) (place-image (circle 10 "solid" "red") 50 50 (empty-scene 100 100))) (define (draw-on lop) (cond [(empty? lop) (empty-scene 100 100)] [(cons? lop) (place-image (circle 10 "solid" "red") (posn-x (first lop)) (posn-y (first lop)) (draw-on (rest lop)))]))
32.4 Designing functions
Design a function that computes the “dot product” of two equal length lists of numbers. The dot product is the sum of the product of each corresponding elements in the lists. For example, the dot product of (list 1 2 3) and (list 4 5 6) is (+ (* 1 4) (* 2 5) (* 3 6)).
(list (list (* 1 4) (* 1 5) (* 1 6) (* 1 7)) (list (* 2 4) (* 2 5) (* 2 6) (* 2 7)) (list (* 3 4) (* 3 5) (* 3 6) (* 3 7)))
Notice that the outer product of a list of length N and of length M is a list of N lists of M numbers, with the exception that if M or N is 0, the result is an empty list.
(list (list "a1" "a2" "a3" "a4") (list "b1" "b2" "b3" "b4") (list "c1" "c2" "c3" "c4"))
Design an abstraction function for “outer-product-like" computations of any kind. Redefine your two outerproduct functions in terms of it.
Design a function append-to-each that consumes a string s and a list of string los and produces a list of strings like los but with s appended to the front of each element.
Design a function append-all that consumes two list of strings los1 and los2 and produces a list of strings that appends each element of los1 to all of the elements in los2. For example, (append-all (list "a" "b") (list "c" "d")) should produce (list "ac" "ad" "bc" "bd").
(list "aa" "ab" "ac" "ba" "bb" "bc" "ca" "cb" "cc")
(list "" "a" "b" "c" "aa" "ab" "ac" "ba" "bb" "bc" "ca" "cb" "cc")
33 November 3, 2017
Audio and video capture from today’s class is available here.
Code from today: qsort.rkt.
34 Solving lab 19: From Functions to Signatures
Lab 19 asks you to provide the most general signature for functions like the following:
; brillig : (define (brillig x) (= 1 (modulo x 2)))
The way to approach problems like this is to play code detective. Start by collect evidence of what you know, then use that to make deductions about other things you know. Keep doing this until you can’t deduce anything more, and you’ve arrived at the most general signature.
Let’s walk through an example. What do you know about brillig? It’s a function that takes one input. Let’s make a signature involving variables to capture what we know so far; as we continue, these variables may get solved and go away. So far we have:
; brillig : A -> B
We know that much just from look at:
(define (brillig x) ...)
Now, let’s look at the body of the function to try and learn more information about A and B.
Q: How is the parameter x used? A: it is the first argument to modulo. Follow-up Q: what is the signature of modulo? A: Number Number -> Number. So we can conclude A = Number.
Q: What kind of value does the body of the function produce? A: It produces whatever kind of value = produces. Follow-up Q: What does = produce? A: A Boolean. So we can conclude B = Boolean.
Since we’ve solved for the two unknowns, A, B, we are done and can now give the most general signature:
; brillig : Number -> Boolean
Using this signature, go back to the code and confirm it makes sense.
Let’s do another.
; slithy : (define (slithy m n) (> (length m) n))
We can see from the form of the definition that slithy is a function taking two arguments. Assigning variables for the unknowns, we get:
; slithy : A B -> C
How are the arguments used?
Well, m is the argument of length and length expects a list of some kind. What kind? We don’t know yet, so assign a new variable for this unknown, say D. Now we know A = [Listof D].
Switching to n, it is the second argument of >, so B = Number.
What kind of value does the body of the function produce? Whatever kind of value > produces, i.e. Booleans.
; slithy : [Listof D] Number -> Boolean
Are there any facts we haven’t accounted for? No, so we’re done, but there are still unkowns: D. Take another look at the code. Does the code impose any constraints on what kind of elements are in the list? Does it treat them like numbers, string, functions, etc.? No, it doesn’t do anything with the elements of the list, so there’s nothing more to learn about D and it remains as a parameter in the most general signature:
; slithy : [D] [Listof D] Number -> Boolean
Go back and make sure this signature makes sense for the function.
Another:
; outgrabe : (define (outgrabe x y) (map x (append y y)))
From the definition, we get:
; outgrabe : A B -> C
How is the first parameter, x, used? It is the first argument of map. The first argument of map must be a function that takes one argument, so we know A must be D -> E where D and E are new unknowns.
How is the second parameter, y, used? It is both the first and second argument of append, which takes two lists and produces a list of the same kind of element. So B must be a list of some kind [Listof F].
Now, since the result of (append y y) is the second argument to map and we know the elements of the list and the input of the function must match, we can conclude F = D.
What about C? What kind of value does the body of the function produce? It produces whatever kind of value map produces, which is a list of elements produced by the given function. Hence, C = Listof E.
; outgrabe : [D -> E] [Listof D] -> [Listof E]
Are there any facts we haven’t accounted for or anything more we can say about D or E? No, so we’re done and D and E are parameters to the signature:
; outgrabe : [D E] [D -> E] [Listof D] -> [Listof E]
Go back and make sure this signature makes sense for the function.
NOTE: It’s important to note that whenever we determine that one variable is equal to another, we then only use one or the other, but not both. For example, we know D = F, but it would be a mistake to give this function the signature:
; WRONG-outgrabe : [D E F] [D -> E] [Listof F] -> [Listof E]
The problem is having two separate parameters, which sould really be a single one, makes it seem like D and E can be instantiated separately to different things. So each set of equal variables, should be represnted by a single variable in the final signature.
Moving on:
; uffish : (define (uffish x) (cond [(number? x) (+ x 10)] [(string? x) (string-length x)]))
We know:
; uffish : A -> B
; A NumOrString is one of ; - A Number ; - A string
What kind of value does the function produce? It produces whatever the cond produces, which in term produces whatever + produces and whatever string-length produces, i.e. Numbers.
; uffish : NumOrString -> Number
; frabjous : (define (frabjous a b c) (a (b c)))
; frabjous : A B C -> D
What do we know about A based on how a is used? It is a function of one argument. So A = E -> F for new unknowns.
; frabjous : [E -> F] B C -> D
What do we know about B based on how b is used? It is a function of one argument. So B = G -> H for new unknowns.
; frabjous : [E -> F] [G -> H] C -> D
What do we know about C based on how c is used? It is the argument of b. So G = C.
; frabjous : [E -> F] [C -> H] C -> D
Are there facts we haven’t accounted for? Yes, the result of (b c) is the argument of a, so the input of a and the result of b must match, i.e. E = H.
; frabjous : [E -> F] [C -> E] C -> D
What does the function produce? Whatever a produces, so D = F.
; frabjous : [E -> D] [C -> E] C -> D
There’s nothing more we can deduce, so the remaining unknowns are parameters:
; frabjous : [C D E] [E -> D] [C -> E] C -> D
Next, picking up the pace:
; callooh : (define (callooh a b) (a 10 (or (b 0) (b 1)))) ; callooh : A B -> C ; because (b 0) and (b 1) ; callooh : A [Numbder -> D] -> C ; because (or (b 0) (b 1)) ; callooh : A [Numbder -> Boolean] -> C ; because (a 10 (or ...)) ; callooh : [Number Boolean -> G] [Numbder -> Boolean] -> C ; because (define (callooh ...) (a ...)) ; callooh : [Number Boolean -> C] [Numbder -> Boolean] -> C ; done: ; callooh : [C] [Number Boolean -> C] [Numbder -> Boolean] -> C
Last:
; callay : (define (callay q) (frabjous (λ (d) (+ d 42)) q "day")) ; callay : A -> B
Now since we apply a function with a parametric signature, we need to use the parameters of frabjous (first making them distinct from the unknowns we have so far, which they already are) and try to solve for them:
frabjous : [E -> D] [C -> E] C -> D
Since "day" is the third argument, C = String.
frabjous : [E -> D] [String -> E] String -> D
Since q is the second argument, A = [String -> E].
Since (λ (d) (+ d 42)) is the first argument, and it has the signature [Number -> Number], we know E = Number and D = Number.
frabjous : [Number -> Number] [String -> Number] String -> Number
Coming back to callay, we know A = [String -> E] and E = Number, so A = [String -> Number]:
; callay : [String -> Number] -> B
What does the function produce? Whatever frabjous produces. So B = Number:
; callay : [String -> Number] -> Number
And we’re done.
35 November 10, 2017
Audio and video capture from today’s class is available here.
36 November 13, 2017
Audio and video capture from today’s class is available here.
37 November 15, 2017
Audio and video capture from today’s class is available here.
38 November 17, 2017
Audio and video capture from today’s class is available here.
Code: graph.rkt.
39 November 20, 2017
Audio and video capture from today’s class is available here.
Code: graph2.rkt.
40 November 27, 2017
Audio and video capture from today’s class is available here.
Code: typed.rkt.
41 November 29, 2017
Audio and video capture from today’s class is available here.
Code: typed2.rkt.
42 December 1, 2017
Audio and video capture from today’s class is available here.
43 December 4, 2017
Audio and video capture from today’s class is available here.
The client has been filled-in to be a full implementation. The server code is as it was in class.
44 Final Exam Drills
The final exam is cumulative, so you should review Midterm 1 Drills and Midterm 2 Drills. The following drills only cover material introduced since the second midterm.
Solutions: drill-final-exam-soln.rkt.
44.1 Designing with accumulators
Here is a design of the factorial function using structural recursion on natural numnbers:
; factorial : Natural -> Natural ; Compute n! (check-expect (factorial 5) 120) (define (factorial n) (cond [(zero? n) 1] [else (* n (factorial (sub1 n)))]))
Design a variant of factorial that uses structural recursion on n with an accumulator that represents the factorial of all the numbers seen so far.
Here is a design of the largest function that uses structural recursion on a non-empty list of (real) numbers to compute the largest number in the list:
; largest : [NEListof Real] -> Real ; Finds largest element in given non-empty list (check-expect (largest (list 7)) 7) (check-expect (largest (list 2 9 7)) 9) (define (largest ns) (cond [(empty? (rest ns)) (first ns)] [else (max (first xs) (largest (rest xs)))]))
Design a variant of largest that uses structural recursion on ns with an accumulator that represents the largest element of the list seen so far.
Here is a design of the prod function that computes the product of a list of numbers:
; prod : [Listof Number] -> Number ; Compute the product of the list (check-expect (prod '()) 1) (check-expect (prod (list 1 2 3 4 5)) 120) (define (prod xs) (cond [(empty? xs) 1] [(cons? xs) (* (first xs) (prod (rest xs)))]))
Here is a design of sum:
; sum : [Listof Number] -> Number ; Compute the sum of the list (check-expect (sum '()) 0) (check-expect (sum (list 1 2 3 4 5)) 15) (define (sum xs) (cond [(empty? xs) 0] [(cons? xs) (+ (first xs) (sum (rest xs)))]))
Give alternative designs that use an accumulator to represent the product (resp. sum) of the numbers seen so far.
Based on your accumulator variant of prod and sum, design an abstraction of these two functions. Give it the most general signature you can. Reformulate your accumulator-based prod and sum functions in terms of this abstraction.
What does the abstraction remind you of?
Can you use your abstraction to reformulate largest?
Here is the design of a function called minf that consumes a function producing real numnbers and a non-empty list of input elements and finds the (earliest) element in the list that minimizes the output of the function:
; minf : [X] [X -> Real] [NEListof X] -> X ; Find the earliest element that minimizes f. (check-expect (minf sqr (list -4 2 8)) 2) (check-expect (minf sqr (list -4 -2 8 2)) -2) (define (minf f xs) (cond [(empty? (rest xs)) (first xs)] [else (local [(define x1 (first xs)) (define y1 (f x1)) (define xn (minf f (rest xs))) (define yn (f xn))] (if (<= y1 yn) x1 xn))]))
The observant reader will notice that function f is called 2 × (n-1) times (where n is the length of the list). Using an accumulator-based design, you can do better, calling the function at most n times. The trick is that you will need two accumulators: the minimizing element seen so far and the result of applying the function to that minimizing element; also note that you start these values off by using the first element of the list (which is guaranteed to exist).
Design a 2-accumulator-based version of minf and argue why it only calls f at most n times.
44.2 Generative recursion
Suppose we have a data definition for "ascening strings," i.e. strings that consist of letters that must appear in alpahabetic order in the string. For example, "aabcz" and "bdrtu" are ascending, but "efarw" is not.
; An AscString is a String ; where (explode s) is sorted by string<?
Design a function that is given an AscString and a 1String and determines if the given letter occurs in the string. It should use generative recursion to be more efficient than scanning the list. (You should not use string-contains?.)
44.3 Invariants
A Quad Tree is an important data structure for representing a set of spatial coordinates, for example a set of GPS locations, and supporting very efficient queries about whether a given point is in the set of locations or not.
The idea is to represent a set of points using a tree. Each node in the tree contains a point and four subtrees. The four subtrees have an important invariant: one holds all the points that are to the Northwest of the point in the node, another holds the points to the Northeast, another the Southeast, and another the Southwest.
Here is a data definition for quad trees:
; A QT (Quad Tree) is one of: ; - #false ; - (make-quad Posn QT QT QT QT) (define-struct quad (pt ne nw se sw)) ; Interp: a set of positions, #false represents an empty set ; Invariant: ; - all points in ne are north (y is smaller) & east (x is larger) of pt ; - all points in nw are north (y is smaller) & west (x is smaller) of pt ; - all points in se are south (y is larger) & east (x is larger) of pt ; - all points in sw are south (y is larger) & west (x is larger) of pt
(Note this uses the convention of graphics coordinates in which the y-axis grows downward.)
Define the following function, taking advantage of this invariant to compute the answer efficiently:
; contains? : Posn QT -> Boolean ; Is the given position in the set?
44.4 Graphs
When we studied graphs we used the follow data representation for graphs (November 20, 2017):
; A Graph is [Listof (cons String [Listof String])] ; Interp: a graph is a list of nodes and neighbors reachable from the node
So a graph such as this:
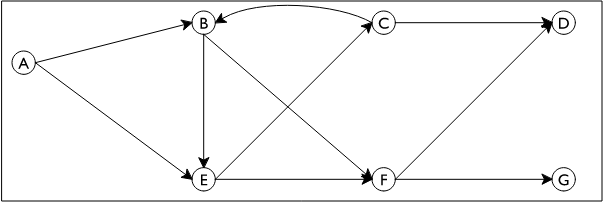
is represented as:
(define G (list (list "A" "B" "E") (list "B" "E" "F") (list "C" "D" "B") (list "D") (list "E" "C" "F") (list "F" "D" "G") (list "G")))
Alternatively, we could have represented a graph as a list of edges:
; A Graph is [Listof (list String String)] ; Interp: a graph is a list of edges from one node to another
Under this definition, the graph above would be represented as:
(define G (list (list "A" "B") (list "A" "E") (list "B" "E") (list "B" "F") (list "C" "D") (list "C" "B") (list "E" "C") (list "E" "F") (list "F" "D") (list "F" "G")))
Re-develop the path function in light of this new representation:
; path : Graph String String -> [Maybe [Listof String]] ; Compute a path in the graph between the given nodes, if one exists ; Produces #false if no path exists
44.5 Types
Which of the following programs well-typed (according to Typed Racket’s type system)?
(: f : (All (A) (Number -> A) -> A)) (define (f x) (x 3)) (: g : (U String Number) -> (U String Number)) (define (g x) (cond [(string? x) (+ x 3)] [(number? x) (string-append "hi" x)])) (: h : (U String Number) -> (U String Number)) (define (h x) (cond [(string? x) (string-append "hi" x)] [(number? x) (+ x 3)])) (: i : Number -> Real) (define (i x) (if (< x 10) (sqr x) (+ x 50))) (: j : Number -> [Listof Number]) (define (j x) (map (λ ([z : (Number -> Number)]) (z x)) (list add1 sqr sqrt))) (: k : Number String -> [Listof String]) (define (k x y) (cons (string-append (number->string x) y)))
Provide the most general valid type signature for the following functions. Provide type annotations needed for any λ parameters.
(define (lengths xs) (map length xs)) (define (total-length xs) (foldr (λ (x t) (+ (length x) t)) 0 xs)) (define (map-f-zero lof) (map (λ (f) (f 0)) lof))
Challenge problem (nothing this tricky will be on the exam): provide the most general type signature and annotions for this function:
; Abstraction of outer "product" computations (define (outer f l1 l2) (cond [(empty? l2) '()] [else (map (λ (m) (map (λ (n) (f m n)) l2)) l1)]))
45 December 11, 2017
For the final lecture, we collectively came up with the following slide to capture what the course has been all about:

46 December 15, 2017
Here are PDFs of the final exam and solution.
Have a great break! It’s been a pleasure teaching this class and I look forward to seeing you in the Spring! – DVH