13 Hustle: heaps and lists
A little and a little, collected together, become a great deal; the heap in the barn consists of single grains, and drop and drop makes an inundation.
13.1 Inductive data
So far all of the data we have considered can fit in a single machine word (64-bits). Well, integers can’t, but we truncated them and only consider, by fiat, those integers that fit into a register.
In the Hustle language, we will add two inductively defined data types, boxes and pairs, which will require us to relax this restriction.
Boxes are like unary pairs, they simply hold a value, which can be projected out. Pairs hold two values which each can be projected out.
To see how values are now inductively defined notice that if you have a value v, you can make another value with (box v). Similarly, if v1 and v2 are values, then so is (cons v1 v2). This suggests the following recursive type definition for values:
; type Value = ; | Integer ; | Boolean ; | Character ; | Eof ; | Void ; | '() ; | (cons Value Value) ; | (box Value)
The new operations include constructors (box e) and (cons e0 e1) and projections (unbox e), (car e), and (cdr e). We’ll also include predicates for identifying boxes and pairs: (box? e) and (cons? e).
Examples
> (unbox (box 7)) 7
> (car (cons 3 4)) 3
> (cdr (cons 3 4)) 4
> (box? (box 7)) #t
> (cons? (cons 3 4)) #t
> (box? (cons 3 4)) #f
> (cons? (box 7)) #f
Usually boxes are mutable data structures, like OCaml’s ref type, but we will examine this aspect later. For now, we treat boxes as immutable data structures.
13.2 Empty lists can be all and end all
While we’ve introduced pairs, you may wonder what about lists? Just as in Racket, lists can be represented by idiomatic uses of cons: a non-empty list is a pair whose car is an element and whose cdr is the rest of the list. What’s left? We need a representation of the empty list!
In Racket, and in our languages, we write this value as '(). There’s nothing particularly special about the empty list value, we just need another distinguished value to designate it.
Using cons and '() in a structured way we can form proper list, among other useful data structures.
We use the following AST data type for Hustle:
#lang racket ;; type Expr = ... | (Lit Datum) ;; type Datum = ... | '() ;; type Op1 = ... | 'box | 'car | 'cdr | 'unbox | 'box? | 'cons? ;; type Op2 = ... | 'cons
13.3 Parsing
Mostly the parser updates for Hustle are uninteresting. We’ve added some new unary and binary primitive names that the parser now recognizes for things like cons, car, cons?, etc., however, one wrinkle is that we now have a very limited form of quote, so it’s worth discussing what this means for the concrete syntax of our language.
13.3.1 Quote and the notion of self-quoting datums
In Racket, some datums are self-quoting, which means they don’t need to be quoted. For example, 5 is a self-quoting datum. You actually can quote 5: '5. This means exactly the same thing as 5. These are two different concrete syntaxes for exactly the same thing: the integer literal 5.
The whole reason for quote is that it is used to indicate when something is a datum when it would otherwise be interpreted as an expression. This becomes relevant we start having datums with parentheses in them because for example the expression (add1 5) and the datum '(add1 5) mean very different things, whereas 5 and '5, do not. So lists (and pairs) are not self-quoting: we are required to use quote when we want to write such datums: (quote (add1 5)), which can also be written in shorthand form as '(add1 5).
Up until this point, all of our datums have been self-quoting and we have thus just left quote out of the concrete syntax. Now we have quote for the empty list.
13.3.2 Parsing quoted datums and self-quoting datums
In our parser, we introduce a predicate for identifying self-quoting datums (self-quoting-datum?), which includes integers, boolean, and characters; and another for identifying the larger class of datums (datum?), which includes all the self-quoting datums, plus the empty list '(). Notice in the parser that self-quoting datums are expressions, but quoted datums must occur withing a (quote ...) form.
Examples
> (parse 5) '#s(Lit 5)
; This is quoting at the Racket-level and the parser sees 5 > (parse '5) '#s(Lit 5)
; This is quoting at the Hustle-level and the parser see '(quote 5) ; which it parses at (Lit 5) > (parse ''5) '#s(Lit 5)
; This is quoting at the Racket-level and the parser see '(), ; but () is not valid expression syntax, hence a parse error > (parse '()) parse error '()
; This is quoting at the Hustle-level and the parser sees '(quote ()), ; which is parsed as the empty list. > (parse ''()) '#s(Lit ())
It’s worth noting that while we have added pairs and boxes to our language, we have not added literal notation for these things. (We will eventually.) So things like '(1 . 2) are not valid syntax in Hustle:
Examples
> (parse ''(1 . 2)) parse error '(1 . 2)
#lang racket (provide parse parse-closed) (require "ast.rkt") ;; s:S-Expr -> e:ClosedExpr ;; Parse s into (a potentially open) expr e (define (parse s) (match (parse/acc s '() '()) [(list _ e) e])) ;; s:S-Expr -> e:ClosedExpr ;; Parse s into closed expr e; signal an error when e is open (define (parse-closed s) (match (parse/acc s '() '()) [(list '() e) e] [(list fvs e) (error "unbound identifiers" fvs)])) ;; s:S-Expr bvs:[Listof Id] fvs:[Listof Id] ;; -> (list fvs-e:[Listof Id] e:Expr) ;; Parse s into expr e and list of free variables fvs-e, ;; assuming variables in bvs are bound and fvs are free. (define (parse/acc s bvs fvs) (define (rec s bvs fvs) (match s [(and 'eof (? (not-in bvs))) (list fvs (Eof))] [(? self-quoting-datum?) (list fvs (Lit s))] [(list (and 'quote (? (not-in bvs))) (? datum? d)) (list fvs (Lit d))] [(? symbol?) (list (if (memq s bvs) fvs (cons s fvs)) (Var s))] [(list-rest (? symbol? (? (not-in bvs) k)) sr) (match k ['let (match sr [(list (list (list (? symbol? x) s1)) s2) (match (parse/acc s1 bvs fvs) [(list fvs e1) (match (parse/acc s2 (cons x bvs) fvs) [(list fvs e2) (list fvs (Let x e1 e2))])])] [_ (error "let: bad syntax" s)])] [_ (match (parse-es/acc sr bvs fvs) [(list fvs es) (list fvs (match (cons k es) [(list (? op0? o)) (Prim0 o)] [(list (? op1? o) e1) (Prim1 o e1)] [(list (? op2? o) e1 e2) (Prim2 o e1 e2)] [(list 'begin e1 e2) (Begin e1 e2)] [(list 'if e1 e2 e3) (If e1 e2 e3)] [_ (error "bad syntax" s)]))])])] [_ (error "parse error" s)])) (rec s bvs fvs)) ;; s:S-Expr bvs:[Listof Id] fvs:[Listof Id] ;; -> (list fvs-e:[Listof Id] es:[Listof Expr]) ;; Parse s into a list of expr es and list of free variables fvs-e, ;; assuming variables in bvs are bound and fvs are free. (define (parse-es/acc s bvs fvs) (match s ['() (list fvs '())] [(cons s ss) (match (parse/acc s bvs fvs) [(list fvs e) (match (parse-es/acc ss bvs fvs) [(list fvs es) (list fvs (cons e es))])])] [_ (error "parse error")])) ;; xs:[Listof Any] -> p:(x:Any -> Boolean) ;; Produce a predicate p for things not in xs (define (not-in xs) (λ (x) (not (memq x xs)))) ;; Any -> Boolean (define (self-quoting-datum? x) (or (exact-integer? x) (boolean? x) (char? x))) ;; Any -> Boolean (define (datum? x) (or (self-quoting-datum? x) (empty? x))) ;; Any -> Boolean (define (op0? x) (memq x '(read-byte peek-byte void))) (define (op1? x) (memq x '(add1 sub1 zero? char? integer->char char->integer write-byte eof-object? box unbox empty? cons? box? car cdr))) (define (op2? x) (memq x '(+ - < = eq? cons)))
13.4 Meaning of Hustle programs, implicitly
To extend our interpreter, we can follow the same pattern we’ve been following so far. We have new kinds of values such as pairs, boxes, and the empty list, so we have to think about how to represent them, but the natural thing to do is to represent them with the corresponding kind of value from Racket. Just as we represent Hustle booleans with Racket booleans, Hustle integers with Racket integers, and so on, we can also represent Hustle pairs with Racket pairs. We can represent Hustle boxes with Racket boxes. We can represent Hustle’s empty list with Racket’s empty list.
Under this choice of representation, there’s very little to do in the interpreter. We only need to update the interpretation of primitives to account for our new primitives such as cons, car, etc. And how should these primitives be interpreted? Using their Racket counterparts of course!
#lang racket (provide interp-prim0 interp-prim1 interp-prim2) ;; Op0 -> Value (define (interp-prim0 op) (match op ['read-byte (read-byte)] ['peek-byte (peek-byte)] ['void (void)])) ;; Op1 Value -> Value { raises 'err } (define (interp-prim1 op v) (match (list op v) [(list 'add1 (? integer?)) (add1 v)] [(list 'sub1 (? integer?)) (sub1 v)] [(list 'zero? (? integer?)) (zero? v)] [(list 'char? v) (char? v)] [(list 'integer->char (? codepoint?)) (integer->char v)] [(list 'char->integer (? char?)) (char->integer v)] [(list 'write-byte (? byte?)) (write-byte v)] [(list 'eof-object? v) (eof-object? v)] [(list 'box v) (box v)] [(list 'unbox (? box?)) (unbox v)] [(list 'car (? pair?)) (car v)] [(list 'cdr (? pair?)) (cdr v)] [(list 'empty? v) (empty? v)] [(list 'cons? v) (cons? v)] [(list 'box? v) (box? v)] [_ (raise 'err)])) ;; Op2 Value Value -> Value { raises 'err } (define (interp-prim2 op v1 v2) (match (list op v1 v2) [(list '+ (? integer?) (? integer?)) (+ v1 v2)] [(list '- (? integer?) (? integer?)) (- v1 v2)] [(list '< (? integer?) (? integer?)) (< v1 v2)] [(list '= (? integer?) (? integer?)) (= v1 v2)] [(list 'eq? v1 v2) (eq? v1 v2)] [(list 'cons v1 v2) (cons v1 v2)] [_ (raise 'err)])) ;; Any -> Boolean (define (codepoint? v) (and (integer? v) (or (<= 0 v 55295) (<= 57344 v 1114111))))
We can try it out:
Examples
> (interp (parse '(cons 1 2))) '(1 . 2)
> (interp (parse '(car (cons 1 2)))) 1
> (interp (parse '(cdr (cons 1 2)))) 2
> (interp (parse '(let ((x (cons 1 2))) (+ (car x) (cdr x))))) 3
Now while this is a perfectly good specification, this interpreter doesn’t really shed light on how constructing inductive data works because it simply uses the mechanism of the defining language to construct it. Inductively defined data is easy to model in this interpreter because we can rely on the mechanisms provided for constructing inductively defined data at the meta-level of Racket.
The real trickiness comes when we want to model such data in an impoverished setting that doesn’t have such things, which of course is the case in assembly.
The main challenge is that a value such as (box v) has a value inside it. Pairs are even worse: (cons v0 v1) has two values inside it. If each value is represented with 64 bits, it would seem a pair takes at a minimum 128-bits to represent (plus we need some bits to indicate this value is a pair). What’s worse, those v0 and v1 may themselves be pairs or boxes. The great power of inductive data is that an arbitrarily large piece of data can be constructed. But it would seem impossible to represent each piece of data with a fixed set of bits.
The solution is to allocate such data in memory, which can in principle be arbitrarily large, and use a pointer to refer to the place in memory that contains the data.
Before tackling the compiler, let’s look at an alternative version of the interpreter that makes explicit a representation of memory and is able to interpret programs that construct and manipulate inductive data without itself relying on those mechanisms.
13.5 Meaning of Hustle programs, explicitly
Let’s develop an alternative interpreter that describes constructing inductive data without itself constructing inductive data.
The key here is to describe explicitly the mechanisms of memory allocation and dereference. Abstractly, memory can be thought of as association between memory addresses and values stored in those addresses. As programs run, there is a current state of the memory, which can be used to look up values (i.e. dereference memory) or to extend by making a new association between an available address and a value (i.e. allocating memory).
The representation of values changes to represent inductive data through pointers to memory:
; type Value* = ; | Integer ; | Boolean ; | Character ; | Eof ; | Void ; | '() ; | (box-ptr Address) ; | (cons-ptr Address) (struct box-ptr (i)) (struct cons-ptr (i)) ; type Address = Natural
Here we have two kinds of pointer values, box pointers and cons pointers. A box value is represented by an address (some natural number) and a tag, the box-ptr constructor, which indicates that the address should be interpreted as the contents of a box. A cons is represented by an address tagged with cons-ptr, indicating that the memory contains a pair of values.
To model memory, we use a list of Value* values. When memory is allocated, new elements are placed at the front of the list. To model memory locations, use the distance from the element to the end of the list, this way addresses don’t change as memory is allocated.
For example, suppose we have allocated memory to hold four values '(97 98 99 100). The address of 100 is 0; the address of 99 is 1; etc. When a new value is allocated, say, '(96 97 98 99), the address of 99 is still 0, and so on. The newly allocated value 96 is at address 4. In this way, memory grows toward higher addresses and the next address to allocate is given by the size of the heap currently in use.
; type Heap = (Listof Value*)
When a program is intepreted, it results in a Value* paired together with a Heap that gives meaning to the addresses in the value, or an error:
; type Answer* = (cons Heap Value*) | 'err
So for example, to represent a box (box 99) we could have a box value, i.e. a tagged pointer that points to memory containing 99:
The value at list index 0 is 99 and the box value points to that element of the heap and indicates it is the contents of a box.
It’s possible that other memory was used in computing this result, so we might end up with an answer like:
Or:
Both of which really mean the same value: (box 99).
A pair contains two values, so a cons-ptr should point to the start of elements that comprise the pair. For example, this answer represents a pair (cons 100 99):
Note that the car of this pair is at address 0 and the cdr is at address 1.
Note that we could have other things residing in memory, but so long as the address points to same values as before, these answers mean the same thing:
In fact, we can reconstruct a Value from a Value* and Heap:
#lang racket (provide unload unload-value) (require "heap.rkt") ;; Answer* -> Answer (define (unload a) (match a ['err 'err] [(cons h v) (unload-value v h)])) ;; Value* Heap -> Value (define (unload-value v h) (match v [(? integer?) v] [(? boolean?) v] [(? char?) v] [(? eof-object?) v] [(? void?) v] ['() '()] [(box-ptr a) (box (unload-value (heap-ref h a) h))] [(cons-ptr a) (cons (unload-value (heap-ref h a) h) (unload-value (heap-ref h (add1 a)) h))]))
Which relies on our interface for heaps:
#lang racket (provide alloc-box alloc-cons heap-ref heap-set (struct-out box-ptr) (struct-out cons-ptr)) (struct box-ptr (i)) (struct cons-ptr (i)) ;; Value* Heap -> Answer* (define (alloc-box v h) (cons (cons v h) (box-ptr (length h)))) ;; Value* Value* Heap -> Answer* (define (alloc-cons v1 v2 h) (cons (cons v2 (cons v1 h)) (cons-ptr (length h)))) ;; Heap Address -> Value* (define (heap-ref h a) (list-ref h (- (length h) (add1 a)))) ;; Heap Address Value* -> Heap (define (heap-set h i v) (list-set h (- (length h) i 1) v)) ;; Heap Address Natural -> [Listof Value*] (define (heap-ref/n h a n) (define (loop n vs) (match n [0 vs] [_ (loop (sub1 n) (cons (heap-ref h (+ a n)) vs))])) (loop n '()))
Try it out:
Examples
> (unload-value (box-ptr 0) (list 99)) '#&99
> (unload-value (cons-ptr 0) (list 99 100)) '(100 . 99)
> (unload-value (cons-ptr 1) (list 97 98 99 100 101)) '(100 . 99)
What about nested pairs like (cons 1 (cons 2 (cons 3 '())))? Well, we already have all the pieces we need to represent values like these.
Examples
> (unload-value (cons-ptr 0) (list '() 3 (cons-ptr 4) 2 (cons-ptr 2) 1)) '(1 2 3)
Notice that this list could laid out in many different ways, but when viewed through the lens of unload-value, they represent the same list:
Examples
> (unload-value (cons-ptr 4) (list (cons-ptr 2) 1 (cons-ptr 0) 2 '() 3)) '(1 2 3)
The idea of the interpreter that explicitly models memory will be thread through a heap that is used to represent the memory allocated by the program. Operations that manipulate or create boxes and pairs will have to be updated to work with this new representation.
So for example, the cons operation should allocate two new memory locations and produce a tagged pointer to the address of the first one. The car operation should dereference the memory pointed to by the given cons-ptr value.
Examples
> (unload (alloc-cons 100 99 '())) '(100 . 99)
> (unload (alloc-box 99 '())) '#&99
Much of the work is handled in the new interp-prims-heap module:
#lang racket (provide interp-prim0 interp-prim1 interp-prim2) (require "heap.rkt") ;; Op0 Heap -> Answer* (define (interp-prim0 op h) (match op ['read-byte (cons h (read-byte))] ['peek-byte (cons h (peek-byte))] ['void (cons h (void))])) ;; Op1 Value* Heap -> Answer* (define (interp-prim1 p v h) (match (list p v) [(list 'add1 (? integer? i)) (cons h (add1 i))] [(list 'sub1 (? integer? i)) (cons h (sub1 i))] [(list 'zero? (? integer? i)) (cons h (zero? i))] [(list 'char? v) (cons h (char? v))] [(list 'char->integer (? char?)) (cons h (char->integer v))] [(list 'integer->char (? codepoint?)) (cons h (integer->char v))] [(list 'eof-object? v) (cons h (eof-object? v))] [(list 'write-byte (? byte?)) (cons h (write-byte v))] [(list 'box v) (alloc-box v h)] [(list 'unbox (box-ptr i)) (cons h (heap-ref h i))] [(list 'car (cons-ptr i)) (cons h (heap-ref h i))] [(list 'cdr (cons-ptr i)) (cons h (heap-ref h (add1 i)))] [(list 'empty? v) (cons h (empty? v))] [_ 'err])) ;; Op2 Value* Value* Heap -> Answer* (define (interp-prim2 p v1 v2 h) (match (list p v1 v2) [(list '+ (? integer? i1) (? integer? i2)) (cons h (+ i1 i2))] [(list '- (? integer? i1) (? integer? i2)) (cons h (- i1 i2))] [(list '< (? integer? i1) (? integer? i2)) (cons h (< i1 i2))] [(list '= (? integer? i1) (? integer? i2)) (cons h (= i1 i2))] [(list 'eq? v1 v2) (match (list v1 v2) [(list (cons-ptr a1) (cons-ptr a2)) (cons h (= a1 a2))] [(list (box-ptr a1) (box-ptr a2)) (cons h (= a1 a2))] [_ (cons h (eqv? v1 v2))])] [(list 'cons v1 v2) (alloc-cons v1 v2 h)] [_ 'err])) ;; Any -> Boolean (define (codepoint? v) (and (integer? v) (or (<= 0 v 55295) (<= 57344 v 1114111))))
Examples
> (unload (interp-prim1 'box 99 '())) '#&99
> (unload (interp-prim2 'cons 100 99 '())) '(100 . 99)
> (unload (match (interp-prim1 'box 99 '()) [(cons h v) (interp-prim1 'unbox v h)])) 99
Finally, we can write the overall interpreter, which threads a heap throughout the interpretation of a program in interp-env-heap. The top-level interp function, which is intended to be equivalent to the original interp function that modelled memory implicitly, calls interp-env-heap with an initially empty heap and the unloads the final answer from the result:
#lang racket (provide interp interp-env-heap) (require "env.rkt") (require "unload.rkt") (require "interp-prims-heap.rkt") (require "ast.rkt") ;; type Answer* = ;; | (cons Heap Value*) ;; | 'err ;; type Value* = ;; | Integer ;; | Boolean ;; | Character ;; | Eof ;; | Void ;; | '() ;; | (box-ptr Address) ;; | (cons-ptr Address) ;; type Address = Natural ;; type Heap = (Listof Value*) ;; type REnv = (Listof (List Id Value*)) ;; Expr -> Answer (define (interp e) (unload (interp-env-heap e '() '()))) ;; Expr REnv Heap -> Answer* (define (interp-env-heap e r h) (match e [(Lit d) (cons h d)] [(Eof) (cons h eof)] [(Var x) (cons h (lookup r x))] [(Prim0 p) (interp-prim0 p h)] [(Prim1 p e) (match (interp-env-heap e r h) ['err 'err] [(cons h v) (interp-prim1 p v h)])] [(Prim2 p e1 e2) (match (interp-env-heap e1 r h) ['err 'err] [(cons h v1) (match (interp-env-heap e2 r h) ['err 'err] [(cons h v2) (interp-prim2 p v1 v2 h)])])] [(If p e1 e2) (match (interp-env-heap p r h) ['err 'err] [(cons h v) (if v (interp-env-heap e1 r h) (interp-env-heap e2 r h))])] [(Begin e1 e2) (match (interp-env-heap e1 r h) ['err 'err] [(cons h _) (interp-env-heap e2 r h)])] [(Let x e1 e2) (match (interp-env-heap e1 r h) ['err 'err] [(cons h v) (interp-env-heap e2 (ext r x v) h)])]))
13.6 Representing Hustle values
Since we have grown the set of values in our langauge, we have to address the issue of how this set of values can be represented at run-time. The new values we’ve added are: the empty lists, pairs, and boxes. Of these, the empty list is straightfoward: it can be represented like any of our other enumerated values: pick an unused bit pattern and designate it as representing the empty list. Boxes and pairs will require some new mechanisms.
13.6.1 The need for memory
There’s an obvious conundrum encountered as soon as you start thinking about representing Hustle values. Remember that values have to fit in a register, i.e. we have at most 64 bits to represent all of our values. We’ve gotten by so far by using some small number of bits to encode the type of the value and the remaining bits to represent the value itself. We now have new kinds of values: pairs and boxes. These are distinct from the existing types of values, so we will need to devote some bits to indicating these new types. But what about the value part? Well a pair contains two values, e.g. (cons 1 2) contains both the value 1 and the value 2. How can we possibly fit both, which each may take up 64 bits, into a single 64-bit register? Even if we were to chop integers down to say 30 bits so that two could fit in a word with type tag bits left over, that only works for pairs of integers, and even then it only works for small integers. You might also be tempted to use more registers to represent values. Perhaps we use two registers to store values. One is unused except in the case of pairs, then each register holds the elements of the pair.
But the true power of these new kinds of values is the ability to construct arbitrarily large collections of data. That power comes from being able to construct a pair of any two values, including other pairs. So while we might be able to find ways of encoding small collections, we have to face the fact that we might construct large collections and that no strategy that depends upon a fixed number of values will suffice.
We need memory. When creating a pair, just like in our explicit heap-based interpreter, we need to allocate memory and think of the pair value as having a pointer to that memory. In this way we can construct arbitrarily large collections of values, bound only by the available memory on our system.
13.6.2 Tagged pointer values
That idea that we can use pointers to memory to represent datatypes like boxes and pairs seems simple enough, but we also still have to deal with the other aspects of our value encoding. Namely, we need to be able to distinguish all of the disjoint datatypes in our language. A pointer is seemingly just an arbitrary 64-bit integer. How can we tell a pointer apart from other bit patterns that represent integers, booleans, characters, etc.?
A memory location is represented (of course, it’s all we have!) as a number. The number refers to some address in memory. On an x86 machine, memory is byte-addressable, which means each address refers to a 1-byte (8-bit) segment of memory. If you have an address and you add 1 to it, you are refering to memory starting 8-bits from the original address.
It’s tempting to follow the approach we’ve already used: shift and tag. In other words, take a pointer, shift it to the left some number of bits and tag the lower bits with a unique pattern to indicate the type as being either a pair or a box.
This worked for things like booleans, characters, eof, void, etc. because we chould shift to the left without losing any information. In the case of integers, we did lose some information: we cut down the range of integer values that are representable in our language. But the integers that were left still made sense.
Unfortunately pointers don’t work that way. If we shift a pointer and bits fall off, we’re no longer pointing at the same memory location. So what are we to do?
There are many options, but we adopt a simple approach. It starts from the observation that we will always allocate memory in multiples of 8 bytes. So if our memory starts out aligned to 8 bytes, then all of the addresses we will reprent will also be aligned to 8 bytes. That means addresses will always end in #b000. We can therefore use these bits to store information without losing any information about the address itself!
The first thing to do is make another distinction in the kind of values in our language. Up until now, each value could be represented in a register alone. We now call such values immediate values.
We introduce a new category of values which are tagged pointer values. Tagged pointers also fit into registers, but they refer to memory so they cannot be understood by the contents of the register alone; we have to take the memory into consideration too.
We will (for now) have two types of tagged pointer values: boxes and pairs.
So we now have a kind of hierarchy of values:
- Values
- Tagged pointers (non-zero in last three bits)
Boxes
Pairs
- Immediates (zero in last three bits)
Integers
Characters
Booleans
...
We will represent this hierarchy by shifting all the immediates over 3 bits and using the lower 3 bits to tag things as either being immediate (tagged #b000) or a box or pair. To recover an immediate value, we just shift back to the right 3 bits.
So for example:
the value #t is represented by the bits #b11000, aka 24.
the value #f is represented by the bits #b111000, aka 56.
the value 0 is represented by the bits #b000, aka 0.
the value 1 is represented by the bits #b10000, aka 16.
the value 5 is represented by the bits #b1010000, aka 80.
the value #\a is represented by the bits #b110000101000, aka 3112.
the value #\b is represented by the bits #b110001001000, aka 3144.
The pointer types will be tagged in the lowest 3 bits. A box value is tagged #b001 and a pair is tagged #b010. The remaining 61 bits will hold a pointer, i.e. an integer denoting an address in memory. To obtain the address, no shifting is done; instead we simply zero-out the tag.
The idea is that the values contained within a box or pair will be located in memory at this address. If the tagged pointer is a box pointer, reading 64 bits from that location in memory will produce the boxed value. If the pointer is a pair pointer, reading the first 64 bits from that location in memory will produce one of the value in the pair and reading the next 64 bits will produce the other. In other words, constructors allocate and initialize memory. Projections dereference memory.
It’s more difficult to construct examples of tagged pointer values because a value’s representation now depends on what’s in memory. Moveover, a value’s representation is no longer unique. We can no longer say things like “the value '(1 . 2) is represented by the bits...” because there are many possible bits that could represent this value.
We can however say that if a memory address holds two consecutive values: 1 and 2, then a value '(1 . 2) may be represented by the bits you get when you tag that pointer as a pair. Let’s use this idea to write some representation examples. These are all stated hypothetically based on what has to be in memory:
if address 0 holds the value #t and address 8 holds the value #f, then the value '(#t . #f) may be represented by the bits #b10, aka 2.
This a perfectly valid, if somewhat unrealistic example. Your operating system is likely not going to let you use address 0 (or 8 for that matter). That’s OK. We don’t really care what the actual address is so long as it’s always divisible by 8. That’s the only thing our encoding scheme depends upon.
Let’s try another example:
if address 98760 holds the value #t and address 98768 holds the value #f, then the value '(#t . #f) may be represented by the bits #b11000000111001010, aka 98762.
A couple things to notice in this example: (1) the address is divisible by 8, (2) the representation of the value '(#t . #f) is not. That’s because we tacked on the cons type tag in unused bits of the pointer. We haven’t lost any information though: to recover the pointer, simply erase the tag (either by or-ing, xor-ing, or subtracting the tag from the tagged pointer; they are all equivalent if the address is divisible by 8 and the tag is less than 8, which it is).
So in general, we have:
if address a is divisible by 8 and holds the value v₁ and address a + 8 holds the value v₂, then the value (cons v₁ v₂) may be represented by the bits (bitwise-xor a #b10).
if address a is divisible by 8 and holds the value v, then the value (box v) may be represented by the bits (bitwise-xor a #b1).
We can also turn things around:
if bits #b11111100100101000 (aka 129320) represents a value, then at address #b11111100100100110 (aka 129318) there is some value v₁ and at #b11111100100101110 (aka 129326) there is some value v₂.
We know this because the bits end in the pair type tag, thus the value represented is a pair and it must be the case that there are two values at the address encoded in the bits.
In general:
if bits b represents a value and (= (bitwise-and b #b111) #b10), then at address (bitwise-xor b #b10) there is some value v₁ and at address (+ (bitwise-xor b #b10) 8) there is some value v₂.
if bits b represents a value and (= (bitwise-and b #b111) #b1), then at address (bitwise-xor b #b1) there is some value v.
OK, we now have a good model of how these new kinds of values can be represented, but how can we actually construct and manipulate them?
13.6.3 A source of free memory
We’ve established how we can use memory to represent boxes and pairs, but it remains to be seen where this memory comes from and how we can use it to construct these kinds of values.
So far, our only ability to allocate memory has come from using the stack. When we push variable bindings or the results of intermediate computations on the stack, we “allocate” memory by using more of the stack space. When we pop these values off, we “deallocate” that memory by making it available to be overwritten by future stack pushes.
Since it seems to be the only game in town, it’s obviously tempting to use the stack to allocate pairs and boxes. But here’s the rub: variable bindings and intermediate results follow a straightforward stack discipline that we can read off from the text of a program. For example, in (let ((x e₁)) e₂), we know that we can push e₁’s value on the stack before executing the code for e₂ and then pop it off at the end of the instructions for the whole let. Likewise in (+ e₁ e₂), we can push e₁’s value on the stack while computing e₂ and then pop it off to do the addition. But with (cons e₁ e₂), if pushed the values of e₁ and e₂ on the stack and then made a tagged pointer to that value, when would we pop it off? Definitely not at the end of the (cons e₁ e₂) expression because after all we need to be able to access the parts of the pair after making it; deallocating then would construct and immediate destroy the pair. On the other hand, not popping at the end of the expression destroys one of our compiler invariants which is that, by the time we get to the end of the instructions for the compiled code of an expression, we have restored the stack to whatever state it was in at the start. If we destroy that, how will variables and binary operations work? Notice the shape of the stack could no longer be read off from the text of a program. Consider:
(let ((x (if (zero? (read-byte)) (cons 1 2) #f))) x)
Where is x’s value on the stack? If we allocate pairs on the stack, there may or may not be a pair sitting before it and there’s no way to know at compile-time. Good luck compiling that variable occurrence!
So... the stack is out. Mostly this is because the lifetime of pointer values is not lexical: it’s not a property of the text of a program, but rather its execution. So we will need another source of free memory; memory that can outlive elements on the stack. We’ll call this memory the heap.
For this, we will turn to our run-time system. Before it calls the compiled code of a program, we will have it allocate a chunk of memory and pass it as an argument to the compiled code. The compiled code will then install that pointer into a designated register, much like how rsp is designated to hold the stack pointer. So instead of doing this in the main entry point of the run-time:
val_t result; |
result = entry(); |
print_result(result); |
We’ll update it to:
heap = malloc(8 * heap_size); // allocate heap |
val_t result; |
result = entry(heap); // pass in pointer to heap |
print_result(result); |
Here we are allocating some number of words of memory (how many words is given by the constant heap_size), via malloc and then calling the compiled code with an argument which is the pointer to this freshly allocated memory. The compiled code can hold on to a pointer to this memory and write into it in to allocate new pairs and boxes.
We will designate the rbx register as the heap pointer register. This is an arbitrary choice, other than the fact that we selected a callee-saved (aka non-volatile) register. This is useful for us because we need the heap pointer to be preserved across calls into the run-time system. Had we designated a caller-save (volatile) register, we’d need to save and restore it ourselves before and after every call. Choosing a non-volatile register does mean we have to save and restore the caller’s rbx, but we do this just once at the beginning and end of the program.
So our top-level compiler looks like this:
; ClosedExpr -> Asm (define (compile e) (prog (Global 'entry) (Label 'entry) ... (Push rbx) ; save the caller's register (Mov rbx rdi) ; install heap pointer (compile-e e '()) ; run! (Pop rbx) ; restore caller's register ... (Ret)))
Now compile-e can produce code that uses the heap pointer in register rbx. If we want to use some of this memory we can write into it, adjust rbx by the amount we just used, and then produce tagged pointers to the location we wrote to.
So for example the following creates a box containing the value 7:
(seq (Mov rax (value->bits 7)) (Mov (Mem rbx 0) rax) ; write '7' into address held by rbx (Mov rax rbx) ; copy pointer into return register (Xor rax type-box) ; tag pointer as a box (Add rbx 8)) ; advance rbx one word
If rax holds a box value, we can “unbox” it by erasing the box tag, leaving just the address of the box contents, then dereferencing the memory:
(seq (Xor rax type-box) ; erase the box tag (Mov rax (Mem rax 0))) ; load memory into rax
As a slight optimization, instead of doing a run-time tag erasure, we can simply adjust the offset by the tag quantity so that reading the contents of a box (or any other pointer value) is a single instruction:
(seq (Mov rax (Mem rax (- type-box)))) ; load memory into rax
Pairs are similar, only they are represented as tagged pointers to two words of memory. Suppose we want to make (cons #t #f):
(seq (Mov rax (value->bits #t)) (Mov (Mem rbx 0) rax) ; write '#t' into address held by rbx (Mov rax (value->bits #f)) (Mov (Mem rbx 8) rax) ; write '#f' into word after address held by rbx (Mov rax rbx) ; copy pointer into return register (Xor rax type-cons) ; tag pointer as a pair (Add rbx 16)) ; advance rbx 2 words
This code writes two words of memory and leaves a tagged pointer in rax.
If rax holds a pair value, we can project out the elements by erasing the pair tag (or adjusting our offset appropriately) and dereferencing either the first or second word of memory:
(seq (Mov rax (Mem rax (- 0 type-cons))) ; load car into rax (Mov rax (Mem rax (- 8 type-cons)))) ; or... load cdr into rax
From here, writing the compiler for box, unbox, cons, car, and cdr is just a matter of putting together pieces we’ve already seen such as evaluating multiple subexpressions and type tag checking before doing projections.
13.6.4 Making examples
It’s more challenging to use asm-interp to actually execute examples since we need some coordination between the run-time system and asm-interp in order to allocate the heap, but for the moment, let’s see how we can effectively work around this coordination to make examples that actually run without using the run-time system.
An alternative to asking the run-time system to allocate memory (which in turn asks our operating system to allocate memory), we can instead bake some memory into the text of our assembly program itself. This ends up as space in the object file of our compiled and assembled program that also holds the instructions for our code. To do this we can create a data section in our code. Up until now our assembly programs have lived in the text section, which is the part that holds instructions to be executed. In contrast, the data section just holds data, not instructions. When the operating system runs our program, it loads the object file into memory, so anything we put into the data section (as well as all of our instructions) are in memory and we can use this memory. Fundamentally it’s no different from the memory allocated by malloc in our run-time system. The key difference is that this space comes from the object file and therefore has to be determine at compile-time rather than at run-time using malloc. Hence it is referred to as static memory.
When constructing an assembly program, we can switch the data section by using the (Data) psuedo-instruction. What this means is that the instructions that follow should be assembled into the data part of the file and not the text (code) part. To switch back to the text section, use the (Text) directive. Within the data section we can use the Dq “instruction” to designate one (64-bit) word of static memory. It’s not actually an instruction (hence the scare-quotes) because it doesn’t execute; instead it says put these bits at this spot in the program. So this sequence:
(seq (Data) (Dq 1) (Dq 2) (Dq 3))
is saying that in the data section there should be three words of memory containing the bits 1, 2, and 3, respectively.
If we want to get a pointer to this memory, we need to name the location with a label and then use the Lea instruction to load it’s address into a register at run-time:
(seq (Data) (Label 'd) (Dq 1) (Dq 2) (Dq 3) (Text) (Lea rax 'd))
Let’s try it out:
Examples
> (asm-interp (prog (Global 'entry) (Label 'entry) (Data) (Label 'd) (Dq 1) (Dq 2) (Dq 3) (Text) (Lea rax 'd) (Ret))) 140203403726992
Now, what we get back is the address of that memory. It’s some arbitrary number (but notice what it is divisible by!).
If we’d like we can dereference that memory to fetch the contents:
Examples
> (asm-interp (prog (Global 'entry) (Label 'entry) (Data) (Label 'd) (Dq 1) (Dq 2) (Dq 3) (Text) (Lea rax 'd) (Mov rax (Mem rax 0)) (Ret))) 1
To do that, let’s just call malloc ourselves!
Examples
> (asm-interp (prog (Global 'entry) (Extern 'malloc) (Label 'entry) (Sub rsp 8) (Mov rdi (* 10 8)) (Call 'malloc) (Add rsp 8) (Ret))) 94319565457904
This sets up a call to malloc(8*10), which allocates 10 words and returns the pointer in rax.
OK, let’s make a pair:
Examples
> (asm-interp (prog (Global 'entry) (Extern 'malloc) (Label 'entry) (Push rbx) (Mov rdi (* 10 8)) (Call 'malloc) (Mov rbx rax) (Mov rax (value->bits #t)) (Mov (Mem rbx 0) rax) ; write #t (Mov rax (value->bits #f)) (Mov (Mem rbx 8) rax) ; write #f (Mov rax rbx) ; copy pointer (Xor rax type-cons) ; tag as pair (Add rbx 16) ; account for memory used (Pop rbx) (Ret))) 94319565472114
This should create a pair that is represented in memory like this:
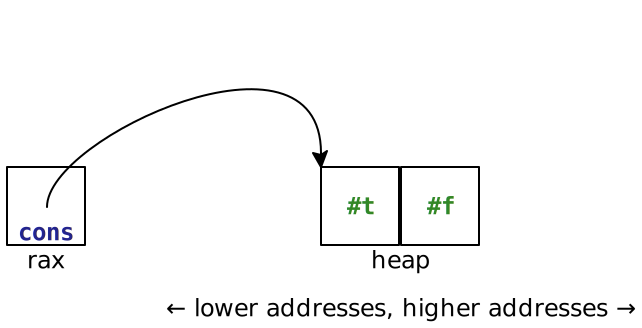
What we get is 94319565472114, which doesn’t look like a pair. But remember, asm-interp is just giving us back whatever is in the rax register after calling this code: it’s giving us back bits, not values. But! You should notice that these bits are encoding a pair value. If we look at the three least significant bits, we see #b010, aka 2:
Examples
> (bitwise-and 94319565472114 #b111) 2
That tells us that #t and #f live at memory addresses (bitwise-xor 94319565472114 #b010) and (+ (bitwise-xor 94319565472114 #b010) 8), respectively.
This is not actually true. Using Racket’s ffi/unsafe library provides a way to cast integers to pointers and dereference arbitrary memory. In fact, ffi/unsafe is the thing that makes asm-interp possible. The memory safety guarantee only applies to programs that safely use ffi/unsafe, which is easiest to do by not using it all!
Now, how can we fetch them? On the Racket side of things, we just have an integer and an integer is not a pointer in Racket. By design, the language does not give you a way to cast an arbitrary integer to some kind of pointer datatype that can be dereferenced. This is important to guarantee memory safety. Of course, asm-interp offers a huge back-door to that safety, so we can whip up our own operation to dereference whatever memory address we’d like:
Examples
; Integer -> Integer ; Fetch the word at given address
> (define (mem-ref ptr) (asm-interp (prog (Global 'entry) (Label 'entry) (Mov r8 ptr) (Mov rax (Mem r8)) (Ret)))) > (mem-ref (bitwise-xor 94319565472114 type-cons)) 24
> (mem-ref (+ (bitwise-xor 94319565472114 type-cons) 8)) 56
And while these also don’t look like #t and #f, remember:
Examples
> (value->bits #t) 24
> (value->bits #f) 56
Aside: We should be very careful with this operation; you can do bad things with it:
Examples
> (mem-ref #xDEADBEEF) invalid memory reference. Some debugging context lost
We’re now in a position to actually reconstruct the pair value on the Racket side of things:
Examples
; Bits -> (cons Value Value) ; Constructs a pair from bits encoding a pair value
> (define (cons-bits->cons b) (cons (bits->value (mem-ref (+ b (- 0 type-cons)))) (bits->value (mem-ref (+ b (- 8 type-cons)))))) > (cons-bits->cons 94319565472114) '(#t . #f)
And this works great so long as the values in the pair aren’t themselves tagged pointers, which of course, they could be! What should we do in that case? Well, figure out what kind of pointer they are, dereference their contents and construct the appropriate kind of Racket value (either a box or a pair). We can do this recursively to complete convert from whatever encoding of a value we get back into the corresponding Racket value. In other words, extending bits->value to work in the presence of tagged pointer values involves just the kind of thing we’ve written:
#lang racket (provide (all-defined-out)) (require ffi/unsafe) (define imm-shift 3) (define imm-mask #b111) (define ptr-mask #b111) (define type-box #b001) (define type-cons #b010) (define int-shift (+ 1 imm-shift)) (define mask-int #b1111) (define char-shift (+ 2 imm-shift)) (define type-int #b0000) (define type-char #b01000) (define mask-char #b11111) ;; Integer -> Value (define (bits->value b) (cond [(= b (value->bits #t)) #t] [(= b (value->bits #f)) #f] [(= b (value->bits eof)) eof] [(= b (value->bits (void))) (void)] [(= b (value->bits '())) '()] [(int-bits? b) (arithmetic-shift b (- int-shift))] [(char-bits? b) (integer->char (arithmetic-shift b (- char-shift)))] [(box-bits? b) (box (bits->value (mem-ref (- b type-box))))] [(cons-bits? b) (cons (bits->value (mem-ref (+ 0 (- b type-cons)))) (bits->value (mem-ref (+ 8 (- b type-cons)))))] [else (error "invalid bits")])) ;; Value -> Integer ;; v must be an immediate (define (value->bits v) (cond [(eq? v #t) #b00011000] [(eq? v #f) #b00111000] [(eq? v eof) #b01011000] [(eq? v (void)) #b01111000] [(eq? v '()) #b10011000] [(integer? v) (arithmetic-shift v int-shift)] [(char? v) (bitwise-ior type-char (arithmetic-shift (char->integer v) char-shift))] [else (error "not an immediate value" v)])) (define (int-bits? v) (= type-int (bitwise-and v mask-int))) (define (char-bits? v) (= type-char (bitwise-and v mask-char))) (define (imm-bits? v) (zero? (bitwise-and v imm-mask))) (define (cons-bits? v) (= type-cons (bitwise-and v imm-mask))) (define (box-bits? v) (= type-box (bitwise-and v imm-mask))) (define (mem-ref i) (ptr-ref (cast i _int64 _pointer) _int64))
You’ll notice that instead of the mem-ref we wrote, it uses Racket’s own “unsafe” operations. The only difference is that this is more efficient, bypassing the overhead of asm-interp.
With bits->value in place, we can now build up some utilities for running programs with the run-time system linked in and using bits->value to construct the result value:
#lang racket (require a86/interp) (require "types.rkt") (require "build-runtime.rkt") (provide run run/io) ;; Run instructions with run-time system linked in ;; Asm -> Answer (define (run is) (match (run/io is "") [(cons r out) (begin (display out) r)])) ;; Run instruction and feed input from string, ;; collection output as a string (useful for testing I/O programs) ;; Asm String -> (cons Answer String) (define (run/io is in) (parameterize ((current-objs (list (path->string runtime-path)))) (match (asm-interp/io is in) [(cons 'err out) (cons 'err out)] [(cons b out) (cons (bits->value b) out)])))
Let’s make the list '(1 2 3). Remember that '(1 2 3) is just (cons 1 (cons 2 (cons 3 '()))).
Examples
> (run (prog (Global 'entry) (Label 'entry) (Push rbx) (Mov rbx rdi) (Mov rax (value->bits 1)) (Mov (Mem rbx 0) rax) (Mov rax rbx) (Add rax (+ 16 type-cons)) (Mov (Mem rbx 8) rax) (Mov rax (value->bits 2)) (Mov (Mem rbx 16) rax) (Mov rax rbx) (Add rax (+ 32 type-cons)) (Mov (Mem rbx 24) rax) (Mov (Mem rbx 24) rax) (Mov rax (value->bits 3)) (Mov (Mem rbx 32) rax) (Mov rax (value->bits '())) (Mov (Mem rbx 40) rax) (Mov rax rbx) (Xor rax type-cons) (Add rbx (* 8 6)) ; account for 6 words used (Pop rbx) (Ret))) '(1 2 3)
These instructions create a list that is laid out in the heap like this:
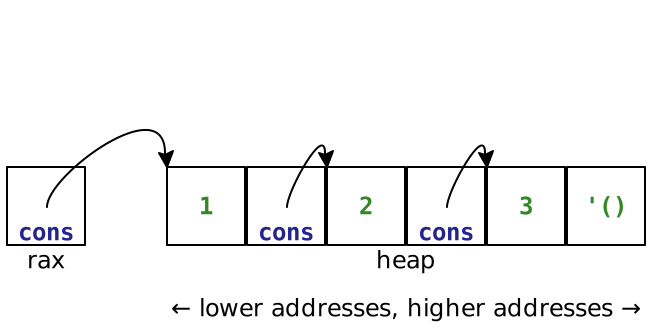
See if you can construct the list this way.
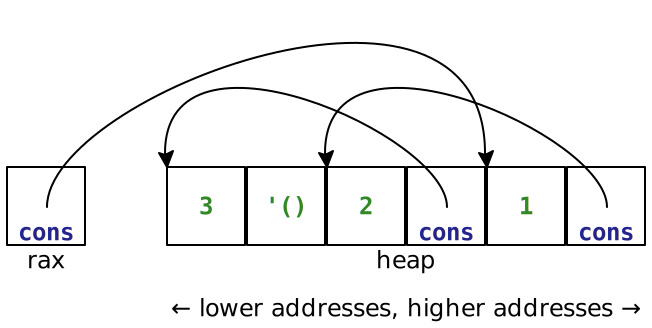
Both of these would result in the same value from the perspective of bits->value.
Now that we can make examples and have a good idea of how to write instructions to create boxes and pairs in memory, let’s write the compiler.
13.7 A Compiler for Hustle
There aren’t any new expression forms in Hustle; all of the work is done in the implementation of the new primitives. Predicates like box?, cons?, and empty? are simple: box? and cons? mask the pointer tag bits and compare against the appropriate tag; empty? tests whether the bits are equal the bits for '().
For box, we know the argument to the box constructor will be in rax register and we need to emit code that will: write that value into memory at the current heap pointer location, move and tag a pointer to that memory into rax, and finally increment rbx to account for the memory used:
Examples
> (compile-op1 'box)
(list
(Mov (Mem 'rbx) 'rax)
(Mov 'rax 'rbx)
(Xor 'rax 1)
(Add 'rbx 8))
> (exec (parse '(box 10))) '#&10
This creates a box value in memory that looks like this:

To unbox a box value, again we have the argument in the rax register. We must check that the argument actually is a box by checking its tag, signalling a run-time type error if its not. If that succeeds, we can dereference the memory by reading the memory location pointed to by the tagged pointer. When dereferencing, we account for the tag by subtracting it as an offset.
Examples
> (compile-op1 'unbox)
(list
(Push 'rax)
(And 'rax 7)
(Cmp 'rax 1)
(Pop 'rax)
(Jne 'err)
(Mov 'rax (Mem 'rax -1)))
> (exec (parse '(unbox (box 10)))) 10
For cons, which is a binary operator, we know the first argument will be the first element of the stack and that the second argument will be in the rax register. The compiler emits code that pops the argument from the stack, writes both to memory, creates a tagged pointer to the memory in rax, and increments rbx by 16 to account for the two words of memory used.
Examples
> (compile-op2 'cons)
(list
(Mov (Mem 'rbx 8) 'rax)
(Pop 'rax)
(Mov (Mem 'rbx 0) 'rax)
(Mov 'rax 'rbx)
(Xor 'rax 2)
(Add 'rbx 16))
> (exec (parse '(cons 1 2))) '(1 . 2)
In order to avoid using a temporary register, this code writes the second argument first, but at offset 8, then pops into rax, writing the first argument second at offset 0. It copies rbx into rax, tags it a pair, then increments rbx appropriately. It creates a pair in memory that looks like this:
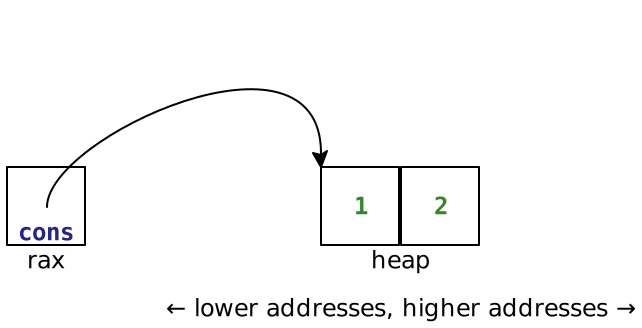
Accessing the parts of a pair is similar to unbox: it checks the type, then reads the memory address at the appropriate offset.
Examples
> (compile-op1 'car)
(list
(Push 'rax)
(And 'rax 7)
(Cmp 'rax 2)
(Pop 'rax)
(Jne 'err)
(Mov 'rax (Mem 'rax -2)))
> (compile-op1 'cdr)
(list
(Push 'rax)
(And 'rax 7)
(Cmp 'rax 2)
(Pop 'rax)
(Jne 'err)
(Mov 'rax (Mem 'rax 6)))
> (exec (parse '(car (cons 1 2)))) 1
> (exec (parse '(cdr (cons 1 2)))) 2
Notice here that in car, the offset is -2, which is (- 0 type-cons), while in cdr it is 6, which is (- 8 type-cons).
We now have all the pieces to make lists or nested lists.
Examples
> (exec (parse '(cons 1 (cons 2 (cons 3 '()))))) '(1 2 3)
Putting it all together we get the compiler for the new primitives: box, unbox, box?, cons, car, car, cdr, cons?, and empty?:
#lang racket (provide compile-op0 compile-op1 compile-op2 pad-stack) (require "ast.rkt") (require "types.rkt") (require "assert.rkt") (require a86/ast a86/registers) ;; Op0 -> Asm (define (compile-op0 p) (match p ['void (seq (Mov rax (value->bits (void))))] ['read-byte (seq (Extern 'read_byte) pad-stack (Call 'read_byte) unpad-stack)] ['peek-byte (seq (Extern 'peek_byte) pad-stack (Call 'peek_byte) unpad-stack)])) ;; Op1 -> Asm (define (compile-op1 p) (match p ['add1 (seq (assert-integer rax) (Add rax (value->bits 1)))] ['sub1 (seq (assert-integer rax) (Sub rax (value->bits 1)))] ['zero? (seq (assert-integer rax) (Cmp rax 0) if-equal)] ['char? (seq (And rax mask-char) (Cmp rax type-char) if-equal)] ['char->integer (seq (assert-char rax) (Sar rax char-shift) (Sal rax int-shift))] ['integer->char (seq (assert-codepoint rax) (Sar rax int-shift) (Sal rax char-shift) (Xor rax type-char))] ['eof-object? (seq (Cmp rax (value->bits eof)) if-equal)] ['write-byte (seq (Extern 'write_byte) (assert-byte rax) pad-stack (Mov rdi rax) (Call 'write_byte) unpad-stack)] ['box (seq (Mov (Mem rbx) rax) ; memory write (Mov rax rbx) ; put box in rax (Xor rax type-box) ; tag as a box (Add rbx 8))] ['unbox (seq (assert-box rax) (Mov rax (Mem rax (- type-box))))] ['car (seq (assert-cons rax) (Mov rax (Mem rax (- 0 type-cons))))] ['cdr (seq (assert-cons rax) (Mov rax (Mem rax (- 8 type-cons))))] ['empty? (seq (Cmp rax (value->bits '())) if-equal)] ['cons? (type-pred ptr-mask type-cons)] ['box? (type-pred ptr-mask type-box)])) ;; Op2 -> Asm (define (compile-op2 p) (match p ['+ (seq (Pop r8) (assert-integer r8) (assert-integer rax) (Add rax r8))] ['- (seq (Pop r8) (assert-integer r8) (assert-integer rax) (Sub r8 rax) (Mov rax r8))] ['< (seq (Pop r8) (assert-integer r8) (assert-integer rax) (Cmp r8 rax) if-lt)] ['= (seq (Pop r8) (assert-integer r8) (assert-integer rax) (Cmp r8 rax) if-equal)] ['cons (seq (Mov (Mem rbx 8) rax) (Pop rax) (Mov (Mem rbx 0) rax) (Mov rax rbx) (Xor rax type-cons) (Add rbx 16))] ['eq? (seq (Pop r8) (Cmp rax r8) if-equal)])) (define (type-pred mask type) (seq (And rax mask) (Cmp rax type) if-equal)) ;; Asm ;; set rax to #t or #f if comparison flag is equal (define if-equal (seq (Mov rax (value->bits #f)) (Mov r9 (value->bits #t)) (Cmove rax r9))) ;; Asm ;; set rax to #t or #f if comparison flag is less than (define if-lt (seq (Mov rax (value->bits #f)) (Mov r9 (value->bits #t)) (Cmovl rax r9))) ;; Asm ;; Dynamically pad the stack to be aligned for a call (define pad-stack (seq (Mov r15 rsp) (And r15 #b1000) (Sub rsp r15))) ;; Asm ;; Undo the stack alignment after a call (define unpad-stack (seq (Add rsp r15)))
13.8 A Run-Time for Hustle
Our compiler relies on the fact that rbx points to available memory, but where did this memory come from? Well that will be the job of the run-time system: before it runs the code our compiler generated, it will ask the operating system to allocate a block of memory and then pass its address as an argument to the entry function the compiler emits.
To allocate memory, it uses malloc. It passes the pointer returned by malloc to the entry function. The protocol for calling functions in the System V ABI says that the first argument will be passed in the rdi register. Since malloc produces 16-byte aligned addresses on 64-bit machines, rdi is initialized with an address that ends in #b000, satisfying our assumption about addresses.
Once the runtime system has provided the heap address in rdi, it becomes our responsibility to keep track of that value. Because rdi is used to pass arguments to C functions, we can’t keep our heap pointer in rdi and expect it to be saved. This leaves us with two options:
We can ensure that we save rdi somewhere safe whenever we might call an external function
We can move the value away from rdi as soon as possible and never have to worry about rdi being clobbered during a call to a C function (as long as we pick a good place!)
We decided to use the second option, which leaves the choice of where to move the value once we receive it from the runtime system. As usual, we will consult the System V Calling Convention, which tells us that rbx is a callee save register, which means that any external function we might call is responsible for ensuring that the value in the register is saved and restored. In other words: we, the caller, don’t have to worry about it! Because of this we’re going to use rbx to store our heap pointer. You can see that we do this in the compiler with (Mov rbx rdi) as part of our entry code.
#include <stdio.h> #include <stdlib.h> #include "values.h" #include "print.h" #include "runtime.h" FILE* in; FILE* out; void (*error_handler)(); val_t *heap; void error_exit() { printf("err\n"); exit(1); } void raise_error() { return error_handler(); } int main(int argc, char** argv) { in = stdin; out = stdout; error_handler = &error_exit; heap = malloc(8 * heap_size); val_t result; result = entry(heap); print_result(result); if (val_typeof(result) != T_VOID) putchar('\n'); free(heap); return 0; }
13.8.1 Updating the run-time system’s notion of Values
We extend our runtime system’s view of values to include pointers and use C struct to represent them:
#ifndef VALUES_H #define VALUES_H #include <stdint.h> /* any abstract value */ typedef int64_t val_t; typedef enum type_t { T_INVALID = -1, /* immediates */ T_INT, T_BOOL, T_CHAR, T_EOF, T_VOID, T_EMPTY, /* pointers */ T_BOX, T_CONS, } type_t; typedef uint32_t val_char_t; typedef struct val_box_t { val_t val; } val_box_t; typedef struct val_cons_t { val_t fst; val_t snd; } val_cons_t; /* return the type of x */ type_t val_typeof(val_t x); /** * Wrap/unwrap values * * The behavior of unwrap functions are undefined on type mismatch. */ int64_t val_unwrap_int(val_t x); val_t val_wrap_int(int64_t i); val_t val_wrap_byte(unsigned char b); int val_unwrap_bool(val_t x); val_t val_wrap_bool(int b); val_char_t val_unwrap_char(val_t x); val_t val_wrap_char(val_char_t b); val_t val_wrap_eof(); val_t val_wrap_void(); val_box_t* val_unwrap_box(val_t x); val_t val_wrap_box(val_box_t* b); val_cons_t* val_unwrap_cons(val_t x); val_t val_wrap_cons(val_cons_t* c); #endif
The implementation of val_typeof is extended to handle pointer types:
#include "types.h" #include "values.h" type_t val_typeof(val_t x) { switch (x & ptr_type_mask) { case box_type_tag: return T_BOX; case cons_type_tag: return T_CONS; } if ((int_type_mask & x) == int_type_tag) return T_INT; if ((char_type_mask & x) == char_type_tag) return T_CHAR; switch (x) { case val_true: case val_false: return T_BOOL; case val_eof: return T_EOF; case val_void: return T_VOID; case val_empty: return T_EMPTY; } return T_INVALID; } int64_t val_unwrap_int(val_t x) { return x >> int_shift; } val_t val_wrap_int(int64_t i) { return (i << int_shift) | int_type_tag; } val_t val_wrap_byte(unsigned char b) { return (b << int_shift) | int_type_tag; } int val_unwrap_bool(val_t x) { return x == val_true; } val_t val_wrap_bool(int b) { return b ? val_true : val_false; } val_char_t val_unwrap_char(val_t x) { return (val_char_t)(x >> char_shift); } val_t val_wrap_char(val_char_t c) { return (((val_t)c) << char_shift) | char_type_tag; } val_t val_wrap_eof(void) { return val_eof; } val_t val_wrap_void(void) { return val_void; } val_box_t* val_unwrap_box(val_t x) { return (val_box_t *)(x ^ box_type_tag); } val_t val_wrap_box(val_box_t* b) { return ((val_t)b) | box_type_tag; } val_cons_t* val_unwrap_cons(val_t x) { return (val_cons_t *)(x ^ cons_type_tag); } val_t val_wrap_cons(val_cons_t *c) { return ((val_t)c) | cons_type_tag; }
13.8.2 Printing Values
Now that values include inductively defined data, the printer must recursively traverse these values to print them (this is exactly analogous to how bits->value had to recursively construct values, too). It also must account for the wrinkle of how the printing of proper and improper lists is different:
#include <stdio.h> #include <inttypes.h> #include "values.h" void print_char(val_char_t); void print_codepoint(val_char_t); void print_cons(val_cons_t *); void print_result_interior(val_t); int utf8_encode_char(val_char_t, char *); void print_result(val_t x) { switch (val_typeof(x)) { case T_INT: printf("%" PRId64, val_unwrap_int(x)); break; case T_BOOL: printf(val_unwrap_bool(x) ? "#t" : "#f"); break; case T_CHAR: print_char(val_unwrap_char(x)); break; case T_EOF: printf("#<eof>"); break; case T_VOID: break; case T_EMPTY: case T_BOX: case T_CONS: printf("'"); print_result_interior(x); break; case T_INVALID: printf("internal error"); } } void print_result_interior(val_t x) { switch (val_typeof(x)) { case T_EMPTY: printf("()"); break; case T_BOX: printf("#&"); print_result_interior(val_unwrap_box(x)->val); break; case T_CONS: printf("("); print_cons(val_unwrap_cons(x)); printf(")"); break; default: print_result(x); } } void print_cons(val_cons_t *cons) { print_result_interior(cons->fst); switch (val_typeof(cons->snd)) { case T_EMPTY: // nothing break; case T_CONS: printf(" "); print_cons(val_unwrap_cons(cons->snd)); break; default: printf(" . "); print_result_interior(cons->snd); break; } } void print_char(val_char_t c) { printf("#\\"); switch (c) { case 0: printf("nul"); break; case 8: printf("backspace"); break; case 9: printf("tab"); break; case 10: printf("newline"); break; case 11: printf("vtab"); break; case 12: printf("page"); break; case 13: printf("return"); break; case 32: printf("space"); break; case 127: printf("rubout"); break; default: print_codepoint(c); } } void print_codepoint(val_char_t c) { char buffer[5] = {0}; utf8_encode_char(c, buffer); printf("%s", buffer); } int utf8_encode_char(val_char_t c, char *buffer) { // Output to buffer using UTF-8 encoding of codepoint // https://en.wikipedia.org/wiki/UTF-8 if (c < 128) { buffer[0] = (char) c; return 1; } else if (c < 2048) { buffer[0] = (char)(c >> 6) | 192; buffer[1] = ((char) c & 63) | 128; return 2; } else if (c < 65536) { buffer[0] = (char)(c >> 12) | 224; buffer[1] = ((char)(c >> 6) & 63) | 128; buffer[2] = ((char) c & 63) | 128; return 3; } else { buffer[0] = (char)(c >> 18) | 240; buffer[1] = ((char)(c >> 12) & 63) | 128; buffer[2] = ((char)(c >> 6) & 63) | 128; buffer[3] = ((char) c & 63) | 128; return 4; } }
13.9 Correctness
The statement of correctness for the Hustle compiler is the same as the previous one, although it is worth noting that it’s use of bits->value within exec/io is hiding some subtleties since it recursively constructs the result value.
FIXME: should this be defined in terms of Answers?
Compiler Correctness: For all e ∈ ClosedExpr, i, o ∈ String, and a ∈ Answer, if (interp/io e i) equals (cons a o), then (exec/io e i) equals (cons a o).
