
| CMSC 131 |  |
| Sections 010X |
Mandelbrot Set
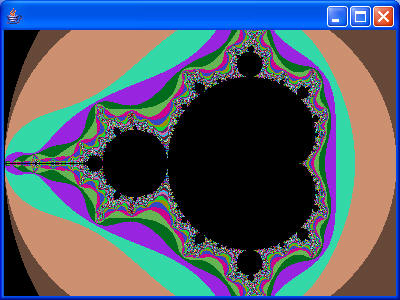
Your project will generate pictures like these:
This is a closed project. Please review the course policy on open/closed projects before you begin.
To practice writing a complete and typical Java class, to practice writing and calling methods of all kinds, and to practice writing JUnit tests to make sure your code is implementing the correct tasks.
The "Mandelbrot Set" was discovered by Benoit Mandelbrot (and others) around 1979. Sadly, Dr. Mandelbrot died recently. He was a fascinating person and a very influential mathematician. Here is a link to a short article about him.
Below is a picture of the entire Mandelbrot Set. The pictures above represent "zooming in" on very tiny portions of the picture below. The black regions in the pictures are the Mandelbrot Set itself; the more colorful parts are also of interest because of the way the colors are chosen.
Amazing Video
If you'd like to see what the mandelbrot set looks like when you zoom in really, really far, check out this AMAZING video which is an animation that zooms in for a very, very long time. The colors chosen for the animation are also really nice. You won't be able to zoom in anywhere near this far with our project because the representation we are using for floating point values does not allow enough precision!
Optional, but strongly recommended reading:
Required reading:
You will be writing two classes, ComplexNumber and MandelbrotTools; and you will be adding additional tests to the JUnit tests file. Follow the instructions below very carefully!
If you do not abide by these rules, you will fail many (if not all) of the release tests!
ComplexNumber class
You must implement all of the data members and methods described below. You may NOT add any instance variables or static variables to this class other than those described below. You may add methods of your own, as long as they are private. NOTE: Not all of the methods described below are required for drawing the Mandelbrot Set, but they must all be implemented correctly as part of this assignment. The class you are writing is a very general class that could be of use in a wide variety of projects, not just for drawing the Mandelbrot Set.
Private Instance Variables
The class will have exactly two instance variables. THESE VARIABLES MUST BE DECLARED PRIVATE AND FINAL! The complex number class you are implementing is an immutable class.
- private final MyDouble real;
- private final MyDouble imag;
These variables represent the state of a complex number. For example, if the current object is supposed to represent the complex number 17.2 + 3.7i, then the value of real would be 17.2, and the value of imag would be 3.7. Note that we have no intention of "storing" the number i -- there is no reason to! The variables are final because once they are set in the constructors, there is no reason to ever change them. (Instance variables that are final can be initialized from within a constructor, but nowhere else.)
Public Constructors
- A standard constructor that takes two parameters (both MyDoubles) representing the real and imaginary components (in that order) that are desired for the ComplexNumber being constructed. The data members real and imag are to be initialized with these values.
- A constructor that takes one parameter (a MyDouble) representing the real component that is desired for the ComplexNumber being constructed. The data member real is to be initialized with that value, but the imag component will be set to zero.
- A copy constructor.
Public Instance Methods
- getReal -- A simple "getter" for the value of the real data member. (This one has a funny name -- GET REAL!)
- getImag -- A simple "getter" for the value of the imag data member.
- add -- this method takes one parameter (a ComplexNumber). It will return a ComplexNumber that is equal to the sum of the current object and the parameter. (Do not modify the current object.)
- subtract -- this method takes one parameter (a ComplexNumber). It will return a ComplexNumber that is computed by subtracting the value of parameter from the current object. (Do not modify the current object.)
- multiply -- this method takes one parameter (a ComplexNumber). It will return a ComplexNumber that represents the product of the current object and the parameter. (Do not modify the current object.)
- divide -- this method takes one parameter (a ComplexNumber). It will return the quotient computed by dividing the current object by the parameter. (Do not modify the current object.)
- equals -- returns true if both fields match. This should be implemented as the .equals has been implemented for other classes during lecture. Use a parameter of type ComplexNumber for this one, even if you have seen this method implemented with type Object sometimes. Unfortunately, we are implementing equals incorrectly for now (we'll learn the right way later in the semester) and so the submit server will display a "FindBugs" warning about it. Please just ignore this warning.
- compareTo -- this method takes one parameter (a ComplexNumber) and returns an int. It will compare the norm of the current object with the norm of the parameter. (See the norm method, below.) If the norms are equal, this method returns 0; if the norm of the current object is less than the norm of the parameter, this method returns -1; if the norm of the current object is greater than the norm of the parameter, this method returns 1.
- toString -- there are four cases here, depending on the signs of the real and imaginary components of the current object. See examples below, which illustrate correct return values for the toString method in each case. Note that there are never any spaces in the value returned. Note there is always a real portion added to the string and an imaginary portion added to the string even if the value in that portion is 0. Note the numeric portion is always explicitly included even if the value is 1.
- "6.7+2.3i"
- "6.7-2.3i"
- "-6.7+2.3i"
- "-6.7-2.3i"
Public Static Methods
- norm -- this method takes one parameter (a ComplexNumber) and returns a MyDouble object representing the norm of the complex number. Recall that for the complex number a + bi, the norm is equal to sqrt(a2 + b2) [The square root of a squared plus b squared.] Note: You may wonder why we are making this method static! That is a good question. We have our reasons...
- parseComplexNumber -- this method takes one parameter (a String) and returns a ComplexNumber. The parameter is a String that represents a complex number, such as "5.9 + 73.44i" or "-2.35 - 6.5i". There could be any number of spaces in the beginning, at the end, before the 'i', and surrounding the '+' and '-' characters. For example, the following Strings could be passed to this method: " - 2.7 + 5.9 i" or possibly: " 79.3 - 5 i" or even: "-1.25-3.469i". The method will parse the String and return a ComplexNumber that represents the value described by the String. You may assume that the String being passed to this method is correctly formatted.
Note: Your method is not expected to handle parameters like "3.2" or "-7.99i" - we would expect those to be passed to this method as something like "3.2 + 0i" or "0 - 7.99i", respectively. Also, your method is not expected to handle parameters like "+3.2+i" - we would expect something like "3.2+1i".
Hint: You will probably want to use some of the methods in the Java String class, so you should probably review the online documentation for the Java String class. Also, you might find it useful to use the static method Double.parseDouble. (See the online documentation for the Java Double class.)
MandelbrotTools class
This class contains just a couple of static methods, described below. You may add other methods, if you wish, as long as they are static and private. You may not add any instance variables or static variables to this class.
Public Static Methods
- isBig -- this method takes one parameter, a ComplexNumber, and will return type boolean. It will do a computation that is very similar to the norm method from the ComplexNumber class. We are not using the norm method here, because finding square roots slows the program down. For the complex number a + bi, this method will compute a2 + b2 , and will compare this value with the static variable called Controller.DIVERGENCE_BOUNDARY, which is built-in to one of the classes we have provided. If a2 + b2 is greater than the value of the variable named DIVERGENCE_BOUNDARY, then the method returns true. Otherwise it returns false.
- divergence -- this method takes one parameter, a ComplexNumber which we will call z0. The method will return type int. This method calculates a sequence of complex numbers z1, z2, z3, z4, etc. as follows:
z1 = z02 + z0
z2 = z12 + z0
z3 = z22 + z0
z4 = z32 + z0
etc.
These values will be computed one by one. After each value is computed, test to see whether or not it isBig (using the previous method). There are two ways for this method to terminate:
- As soon as one of the terms in the sequence isBig, exit the method immediately. In this case, the return value will be the index of the term that was too big. For example, if terms z0 through z34 are all not too big, but term z35 is too big, then you should return 35.
- There is a static variable of type int that we have provided called Controller.LIMIT. Suppose that Controller.LIMIT is 255, which is typical. In that case, if you get all the way through the first 256 terms z0, z1, z2, z3, z4, ... z254, z255 and none of them isBig then the method should terminate, returning -1.
We have provided a class called "Controller", which contains a static main method. After you have finished writing the two classes described above, running this main method will display the following dialog box:
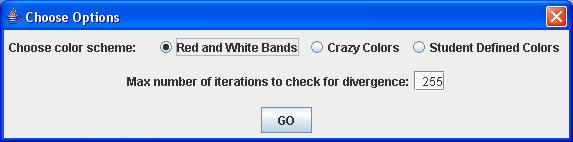
Once the user clicks "Go", the program will draw the Mandelbrot Set, using the color scheme selected. Each time the Mandelbrot set is drawn, you may use the mouse to select a rectangular region to zoom in on, and the program will re-draw the image. This can be repeated many times, but eventually you will exceed the precision of numbers stored in the MyDouble class, and the images will become pixelated. You can also re-size the window so that the pictures are larger or smaller. Small sizes are drawn quickly, but a full-screen view of the Mandelbrot Set is very spectacular to see!
With this project, we have included a couple of JUnit tests that are "public". The code for these tests has been distributed with the project (see the file PublicTests.java). You can run these tests yourself in Eclipse by opening the file, and from the menu selecting: Run, Run As, JUnit Test.
You must add additional JUnit tests to this file that will determine if each of your complex number operations are correct. The tests that should be included are testAdd, testSubtract, testMult, testDiv, testEqComp (equals and compareTo together), testNorm, and testParse. These seven JUnit tests need to be able to test the methods of the ComplexNumber class that you are writing. They should test a variety of different situations. You may add additional methods if you would like, but these must be included. Make sure you are testing more than one set of values for each of the methods - one test case is not usually enough to determine if it works correctly. Look for as much variety as possible in your test cases to ensure a higher level of confidence that your code works as described.
This part is optional, but we'd like you to have some fun being creative!
Create your own color scheme by editing the section that is clearly labeled in the getColor method of the MandelbrotTools class. This method selects a non-black color for a point which DIVERGED when tested with the Mandelbrot recurrence, based on how many terms in the sequence were computed before the terms got "too big". If you put your own code into the section labeled "modify this block to create your own color scheme", then when the user selects "Student Defined Colors" when the program runs, the colors drawn will be determined by your code.
The parameter to the getColor method represents the index of the term in the sequence which was first to be "too big". This value could be anything from 0 up to the constant Controller.LIMIT, which is typically 255 (but could be anything large). For example, if the parameter is 27, that means that z27 was the first term in the sequence that was "too big" for the point that is being colored.
The return value is the Color to be used to color the point. To get an idea of how to create Color objects, you should read the online documentation for the Java Color class API, and also take a look at the two color schemes that are already built into this method (Red and White Bands, Crazy Colors).
Your grade will be determined as follows: