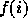 and
and 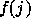 , where i and j are free in
F. Let
, where i and j are free in
F. Let 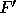 be F with
be F with 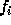 and
and 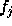 substituted for
substituted for 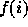 and
and 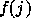 . F if satisfiable iff
. F if satisfiable iff 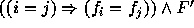 is satisfiable. For more details, see [Sho79].
is satisfiable. For more details, see [Sho79].
The Omega Calculator allows certain restricted uses of uninterpreted function symbols in a Presburger formula. Functions may be declared in the symbolic statement as
symbolic Function ( Arity)where Function is the function name and Arity is its number of arguments. Functions of arity 0 are symbolic constants.
Functions may only be applied to a prefix of the input or output tuple of a relation, or a prefix of the tuple of a set. The function application may list the names of the argument variables explicitly ( not yet supported), or use the abbreviations Function( In), Function( Out), and Function( Set), to describe the application of a function to the appropriate length prefix of the desired tuple.
Our system relies on the following observation: Consider a formula F
that contains references 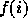 and
and 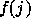 , where i and j are free in
F. Let
, where i and j are free in
F. Let 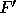 be F with
be F with 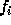 and
and 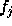 substituted for
substituted for 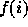 and
and 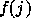 . F if satisfiable iff
. F if satisfiable iff 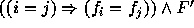 is satisfiable. For more details, see [Sho79].
is satisfiable. For more details, see [Sho79].
Presburger Arithmetic with uninterpreted function symbols is in general undecidable, so in some circumstances we will have to produce approximate results (as we do with the transitive closure operation) [KPRS95].
The following examples show some legal uses of uninterpreted function symbols in the Omega Calculator:
# symbolic p(2), n, m;
#
# R := { [ir,jr] : 1 <= ir <= n && 1 <= jr <= m };
#
# W1 := { [iw,jw] : 1 <= iw <= n && 1 <= jw <= m && p(Set) >= 0 };
#
# W2 := { [iw,jw] : 1 <= iw <= n && 1 <= jw <= m && p(Set) < 0 };
#
# Exposed := R intersection complement ( W1 union W2 );
#
# Exposed;
{[In_1,In_2] : FALSE }
#
#
# symbolic f(1);
#
# R1 := { [i] -> [j] : 1 <= i = j <= 100 && f(In) <= f(Out)};
#
# R2 := { [i] -> [j] : 1 <= i <= j <= 100 && f(In) = f(Out)};
#
#
# R1 intersection R2;
{[i] -> [i] : 1 <= i <= 100}
#
# R1 union R2;
{[i] -> [j] : f(j) = f(i) && 1 <= i < j <= 100} union
{[i] -> [i] : 1 <= i <= 100}
#
# R1 intersection complement R2;
{[i] -> [j] : FALSE }
#
# R1;
{[i] -> [i] : 1 <= i <= 100}