 , Relation &r
, Relation &r )
)
Works for both relations and sets. The arguments must have the same arity. If
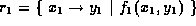 and
and
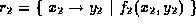 then the result
is
then the result
is 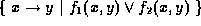 .
.
 , Relation &r
, Relation &r )
)
Works for both relations and sets. The arguments must have the same arity. If
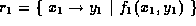 and
and
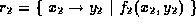 then the result
is
then the result
is 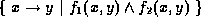 .
.
 , Relation &r
, Relation &r )
)
Works for relations only. The output arity of r
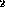 must be same as the input arity of r
must be same as the input arity of r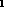 .
If
.
If 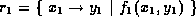 and
and
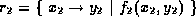 then the result is
then the result is
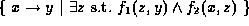 .
.
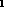 , Relation &r
, Relation &r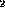 )
)
Equivalent to Composition(r
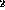 , r
, r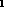 )
.
)
.
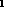 , Relation &r
, Relation &r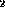 )
)
First argument must be a relation and second argument must be a set. The input arity of r
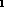 must be the same as the arity of r
must be the same as the arity of r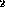 .
If
.
If 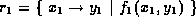 and
and
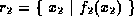 then the result is
then the result is
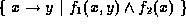 .
.
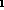 , Relation &r
, Relation &r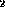 )
)
First argument must be a relation and second argument must be a set. The output arity of r
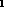 must be the same as the arity of r
must be the same as the arity of r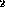 .
If
.
If 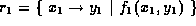 and
and
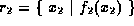 then the result is
then the result is
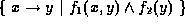 .
.
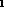 , Relation &r
, Relation &r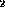 )
)
Works for both relations and sets. The arguments must have the same arity. If
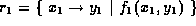 and
and 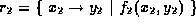 then the result
is
then the result
is 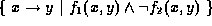 .
.
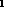 , Relation &r
, Relation &r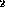 )
)
Works for sets only. If
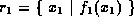 and
and
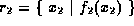 then the result is
then the result is
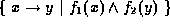 .
.
 , Relation &r
, Relation &r , int effort=0)
, int effort=0)
Works for both relations and sets. The arguments must have the same arity. If
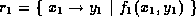 and
and 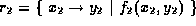 then the result
is
then the result
is 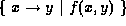 where f is a presburger formula such that
where f is a presburger formula such that
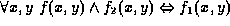 Note: there are many f's that satisfy this property,
so the results of this operation are not completely specified.
We did this deliberately as our method for computing f may change in future
releases.
The effort parameter specifies how hard we try to make f tight,
0 represents least effort and 2 represents most effort.
Note: there are many f's that satisfy this property,
so the results of this operation are not completely specified.
We did this deliberately as our method for computing f may change in future
releases.
The effort parameter specifies how hard we try to make f tight,
0 represents least effort and 2 represents most effort.