- (i)
- Please draw all valid AVL trees containing
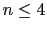 nodes.
nodes.
- (ii)
- This was on the exam, but most students didn't get to it...
Recall that
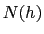 is defined to be the minumum number of nodes in an AVL tree of
height
is defined to be the minumum number of nodes in an AVL tree of
height 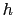 , and that
, and that
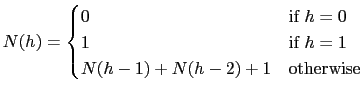
Prove by induction that
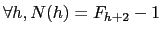 .
.
- (iii)
- The following is a corollary of Binet's Formula:
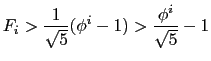
(This is because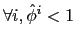 .) Using this corollary and Part (ii)
above, show that the worst-case height of an AVL tree with
.) Using this corollary and Part (ii)
above, show that the worst-case height of an AVL tree with 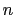 nodes is
nodes is
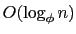 (which implies that any search/insert/delete operation will run in
(which implies that any search/insert/delete operation will run in
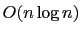 .
.
- (i)
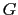 has an Eulerian cycle, but not a Hamiltonian cycle.
has an Eulerian cycle, but not a Hamiltonian cycle.
- (ii)
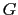 has a Hamiltonian cycle, but not an Eulerian cycle.
has a Hamiltonian cycle, but not an Eulerian cycle.
- (iii)
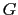 has both an Eulerian and a Hamiltonian cycle.
has both an Eulerian and a Hamiltonian cycle.
def tree_grow(start):
reached = {}
fringe = {start}
while fringe is non-empty:
curr = "get next node" from fringe
fringe = fringe - {curr}
"process" curr
reached = reached U {curr}
for all children c of curr:
if c "is interesting" and c is not in reached:
fringe = fringe U {c}
For each of the following algorithms, explain how to implement the quoted primatives in the tree-growing algorithm. The first one is done for you:
- Depth-First Search (print the current node at each step in the traversal)
- ``get next node'' - the fringe is a stack. Getting the next node is just peeking at the top of the stack, assuming that node has not been reached already.
- ``process'' - here, just print the current node.
- ``is interesting'' - children here are always interesting, as long as they are not already reached.
- Breadth-First Search (print the current node at each step in the traversal)
- ``get next node'' -
- ``process'' -
- ``is interesting'' -
- Prim's algorithm for MST
- ``get next node'' -
- ``process'' -
- ``is interesting'' -
- Dijkstra's algorithm for Shortest Path
- ``get next node'' -
- ``process'' -
- ``is interesting'' -
- ``get next node'' -
- ``process'' -
- ``is interesting'' -
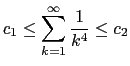
Note: Giving values of
Hint: check the Wikipedia page linked to the course resource page, and feel free
to search a table of integrals if you forget that the antiderivative of ![]() is
is
![]() plus a constant, of course.
plus a constant, of course.
Extra hint from Greg: this problem is hard. Directly applying the integration method (as defined on Wikipedia) will make you a little bit unhappy (try it to find out why). But, one can resolve this by cleverly splitting the summation into two pieces...