

Next: About this document ...
Up: nasty-nums
Previous: Floating Point Problems
As mentioned previously, and repeated for your convenience,
an IEEE single precision floating point number, z, is stored in 32 bits,
with parts s, the sign bit; e, the 8-bit excess-127 exponent;
and, f, the 23 bit fractional part as shown below.
Since all of the 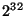 bit patterns are accounted for above, we must set
aside several exceptional or signal values which are interpreted by
the rules below, instead of the simple-minded formula above.
bit patterns are accounted for above, we must set
aside several exceptional or signal values which are interpreted by
the rules below, instead of the simple-minded formula above.
| s |
e |
f |
Meaning |
| 0/1 |
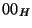 |
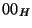 |
Zero |
| 0/1 |
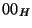 |
non-zero |
DeNormalized |
| 0 |
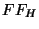 |
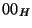 |
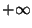 |
| 1 |
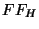 |
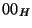 |
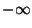 |
| 0/1 |
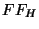 |
non-zero |
Not a Number (NaN) |
- Why must zero be a ``signal'' value?
- What is the largest exponent that can be represented for a normalized floating
point number? What value of e is stored corresponding to this exponent?
- What is the smallest (most negative) exponent that can be
represented, and what value of e is stored for this exponent?
- Give an example of a denormalized floating point number and indicate
how it would be stored.


Next: About this document ...
Up: nasty-nums
Previous: Floating Point Problems
MM Hugue
2004-09-08
![]() bit patterns are accounted for above, we must set
aside several exceptional or signal values which are interpreted by
the rules below, instead of the simple-minded formula above.
bit patterns are accounted for above, we must set
aside several exceptional or signal values which are interpreted by
the rules below, instead of the simple-minded formula above.