This post summarizes some of the kea ideas in our recent paper, Principles of Dataset Versioning: Exploring the Recreation/Storage Tradeoff, to appear in VLDB 2015 (co-authored with: Souvik Bhattacherjee, Amit Chavan, Silu Huang, and Aditya Parameswaran).

The relative ease of collaborative data science and analysis has led to a proliferation of many thousands or millions of versions of the same datasets in many scientific and commercial domains, acquired or constructed at various stages of data analysis across many users, and often over long periods of time. The ability to manage a large number of datasets, their versions, and derived datasets, is a key foundational piece of a system we are building for facilitating collaborative data science, called DataHub. One of the key challenges in building such a system is keeping track of all the datasets and their versions, storing them compactly, and querying over them or retrieving them for analysis.

TL;DR: Version Control Systems (VCS) like Git, SVN, Mercurial, etc., that were primarily designed for source code version control, appear suited for dataset version management as well; however, those have significant limitations for this purpose and are rarely used (instead, most users rely on file systems and manually keep track of the datasets and the versions, leading to significant duplication and other problems). Many of the limitations stem from the assumption that the files being stored are relatively small text files with localized changes; data science applications, on the other hand, typically feature a range of large datasets from unstructured text files to structured database tables and the change patterns tend to be more complex. The algorithms used by those systems also tend to be simplistic and greedy (as we discuss in more detail below), leading to significantly suboptimal behavior with large datasets. Data analysts also need richer retrieval and querying functionality, since there is often a need to cross-analyze the data in multiple files. Finally, the VCS systems have limited support for provenance queries; in data science applications, the ability to reason about the origins of a specific line or record is quite crucial. Our recent TaPP 2015 paper lists many examples for the last two, along with a proposal for a query language.

In the rest of the post, we focus on a specific technical problem: given a collection of datasets and any versioning information among them, how to store them and retrieve specific datasets. There are two conflicting optimization goals here:

  • Minimize the Total Storage Cost: Here we simply measure the total storage as the number of bytes required to store all the information. This has been the primary motivation for much of the work on storage deduplication, which is covered in-depth in a recent survey by Paulo and Pereira.

  • Minimize Recreation Cost, i.e., the Cost of Recreating Versions: This is somewhat trickier to define. First, we may want to minimize the average recreation cost over all datasets, or the maximum over them, or some weighted average (with higher weight given to newer versions). Second, how to measure the recreation cost is not always clear. Should we look at the wall-clock time, the amount of data that needs to be retrieved, or some other metric that considers the CPU cycles or network I/O needed, etc. For the rest of this post, we will assume that recreation cost is equal to the total number of bytes that need to be fetched from the disk. The algorithms that we develop in the paper are more general, and can handle arbitrary recreation costs.

The fundamental challenge here is the storage-recreation trade-off: the more storage we use, the faster it is to recreate or retrieve datasets, while the less storage we use, the slower it is to recreate or retrieve datasets. Despite the fundamental nature of this problem, there has been a surprisingly little amount of work on it.

The first figure below shows an example with 5 datasets (also referred to as files or objects below). Each vertex in the graph corresponds to a dataset and the associated number is the size of the dataset (in bytes). A directed edge from u to v is annotated with the size of the delta required to reconstruct v from u. The delta required to construct u from v is usually different from that required to construct v from u (the standard UNIX diff generates a union of those two directional deltas by default, but can be made to generate one-way deltas as well).

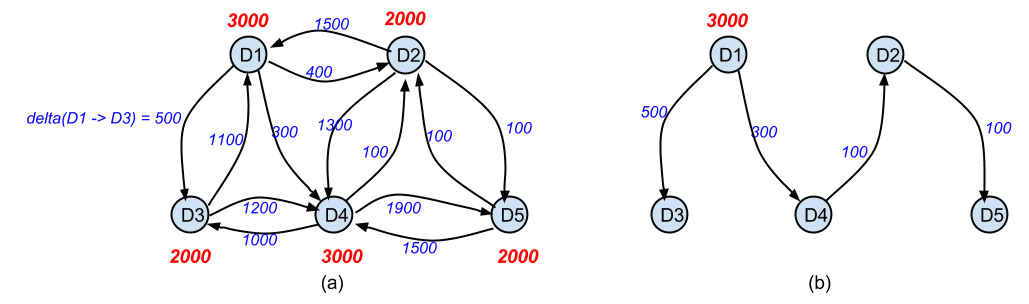
Example

One extreme in terms of storing these datasets is to store each dataset by itself, ignoring any overlaps between them. This results in a total storage cost of 12000 and average recreation cost of 12000/5 = 2400. The other extreme is to store only one dataset by itself, and store the others using deltas from that one. The right figure above shows one example, where D1 is stored by itself; for D3 and D4, a delta from D1 is stored; for D2, a delta from D4 is stored, and finally for D5, a delta from D2 is stored. So to reconstruct D2, we have to first fetch D1 and the delta from D1 to D4 and reconstruct D4, and then fetch the delta from D4 to D2 and use that reconstruct D2. The total storage cost here is 3000+500+300+100+100=4000, much lower than the above option. But the recreation costs here are: (1) D1 = 3000, (2) D3 = 3000 + 500 = 3500, (3) D4 = 3300, (4) D2 = 3000 + 300 + 100 = 3400, and (5) D5 = 3500, with the average being 3340. Using multiple roots gives in-between solutions.

For a larger number of datasets, the differences between the two extremes are much higher. For one of the workloads we used in our paper containing about 100,000 versions with an average size of about 350MB, the storage requirements of the two extreme solutions were 34TB (store all datasets separately) vs 1.26TB (best storage space solution, and the average recreation costs were 350MB vs 115GB !!

Observation: It is easy to show that the best storage is achieved by finding what is the called the minimum cost arborescence (MCA) in this graph (an arborescence is a directed analogue of a spanning tree), which can be found in polynomial time (given all the delta sizes). However that typically does not have a good recreation cost. Balancing the two (e.g., by asking to find the best storage solution that satisfies some bound on the average recreation cost) is typically NP-Hard. See our paper for more details.

Version Control Systems (VCS) like Git, SVN, or Mercurial, are also faced with this problem and they use different greedy heuristics to solve it. Some of these algorithms are not well-documented. Below we briefly discuss the solutions employed by git and svn, and then recap a couple of the experiments from our paper, where we discuss this overall problem and different solutions to it in much more detail.

Git repack

Git uses delta compression to reduce the amount of storage required to store a large number of files (objects) that contain duplicated information. However, git’s algorithm for doing so is not clearly described anywhere. An old discussion with Linus has a sketch of the algorithm. However there have been several changes to the heuristics used that don’t appear to be documented anywhere.

The following describes our understanding of the algorithm based on the latest git source code (Cloned from git repository on 5/11/2015, commit id: 8440f74997cf7958c7e8ec853f590828085049b8).

Here we focus on repack, where the decisions are made for a large group of objects. However, the same algorithm appears to be used for normal commits as well. Most of the algorithm code is in file: builtin/pack-objects.c

Sketch: At a high level, the algorithm goes over the files/objects in some order, and for each object, it greedily picks one of the prior W objects as its parent (i.e., it stores a delta from that object to the object under consideration). As an example, let the order be D1, D4, D2, D3, D5 for the example above. D1 would then be picked as a root. For D4, there is only one option and we will store a delta from D1 to D4. For D2, we choose between D4 and D1; although the delta from D4 is smaller, it also results in a longer delta chain, so a decision is made based on a formula as discussed below.

Details follow.

Step 1

Sort the objects, first by type, then by name hash, and then by size (in the decreasing order). The comparator is (line 1503): static int type_size_sort(const void *_a, const void *_b) Note the name hash is not a true hash; the pack_name_hash() function simply creates a number from the last 16 non-white space characters, with the last characters counting the most (so all files with the same suffix, e.g., .c, will sort together).

Step 2

The next key function is ll_find_deltas(), which goes over the files in the sorted order. It maintains a list of W objects (W = window size, default 10) at all times. For the next object, say $O$, it finds the delta between $O$ and each of the objects, say $B$, in the window; it chooses the the object with the minimum value of: delta(B, O) / (max\_depth - depth of B) where max_depth is a parameter (default 50), and depth of B refers to the length of delta chain between a root and B.

The original repack algorithm appears to have only used delta(B, O) to make the decision, but the depth bias (denominator) was added at a later point to give preference to smaller delta chains even if the corresponding delta was slightly larger.

The key lines for the above part:

  • line 1812 (check each object in the window): ret = try_delta(n, m, max_depth, &mem_usage);

  • lines 1617-1618 (depth bias): ` max_size = (uint64_t)max_size * (max_depth - src->depth) / (max_depth - ref_depth + 1);`

  • line 1678 (compute delta and compare size): ` delta_buf = create_delta(src->index, trg->data, trg_size, &delta_size, max_size);`

create_delta() returns non-null only if the new delta being tried is smaller than the current delta (modulo depth bias), specifically, only if the size of the new delta is less than max_size argument.

Note: lines 1682-1688 appear redundant (the condition would never evaluate to true) given the depth bias calculations.

Step 3

Originally the window was just the last W objects before the object O under consideration. However, the current algorithm shuffles the objects in the window based on the choices made. Specifically, let b_1, …, b_W be the current objects in the window. Let the object chosen to delta against for O be b_i. Then b_i would be moved to the end of the list, so the new list would be: b_1, b_2, …, b_{i-1}, b_{i+1}, …, b_W, O, b_i. Then when we move to the new object after O (say O’), we slide the window and so the new window then would be: b_2, …, b_{i-1}, b_{i+1}, …, b_W, O, b_i, O’.

Small detail: the list is actually maintained as a circular buffer so the list doesn’‘t have to be physically shifted (moving b_i to the end does involve a shift though). Relevant code here is lines 1854-1861.

Finally we note that git never considers/computes/stores a delta between two objects of different types, and it does the above in a multi-threaded fashion, by partitioning the work among a given number of threads. Each of the threads operates independently of the others.

SVN

SVN also uses delta compression, using a technique called skip-deltas that ensures that the delta chains are never too long (specifically, no more than logarithmic in the number of versions). The specifics depend on which backend is being used, and a detailed discussed can be found on the SVN website. This technique does not look at the file contents when making the decisions of which deltas to use, and can require very high storage for long version chains. It is also not clear how to use this technique when there is no clear versioning relationship between the files.

Comparison with SVN and Git

We discuss the results of one experiment here, to illustrate the inefficiencies of the existing solutions and the benefits of careful optimizations. We take 100 forks of the Linux repository, and For each of those, we checkout the latest version and concatenate all files in it (by traversing the directory structure in lexicographic order). Thereafter, we compute deltas between all pairs of versions in a repository. This gives us a workload with 100 files, with an average size of 422MB.

SVN: We create an FSFS-type repository in SVN (v1.8.8), which is more space efficient that a Berkeley DB-based repository. We then import the entire LF dataset into the repository in a single commit. The amount of space occupied by the db/revs/ directory is around 8.5GB and it takes around 48 minutes to complete the import. We contrast this with the naive approach of applying a gzip on the files which results in total compressed storage of 10.2GB. The main reason behind SVN’s poor performance is its use of skip-deltas to ensure that at most O(log n) deltas are needed for reconstructing any version; that tends to lead it to repeatedly store redundant delta information as a result of which the total space requirement increases significantly.

Git: In case of Git (v1.7.1), we add and commit the files in the repository and then run a git repack -a -d --depth=50 --window=50 on the repository. The size of the Git pack file is 202 MB although the repack consumes 55GB memory and takes 114 minutes (for higher window sizes, Git fails to complete the repack as it runs out of memory).

MCA: In comparison, the solution found by the MCA algorithm (i.e., the optimal storage solution as found by our system) occupies 159MB using xdiff from LibXDiff library for computing the deltas; xdiff also forms the basis of Git’s delta computing routine. The total time taken is around 102 minutes; this includes the time taken to compute the deltas and then to find the MCA for the corresponding graph.

Discussion

In our paper linked above, we present a much more detailed experimental comparisons over several other datasets, where we evaluate the trade-offs between storage and recreation costs more thoroughly; one of the algorithms we compare with is our reimplementation of the above git heuristic. Our detailed experiment shows that our implementation of that heuristic (GitH) required more storage than our proposed heuristic, called LMG, for guaranteeing similar recreation costs.