Hat Problems
Derandomiation of Auctions
by Aggarwal, Fiat, Goldberg, Hartline, Immorlica, Sudan. HAT PROBLEM: n people, c colors, simul,
want that for each color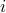 
, 
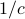of color 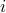them get it right.
They give easy randomized alg then deterministic one.
Hat Guessing Games by Butler, Hajiaghahi, Kleinberg, Leighton.
SIAM Journal of discrete math, Vol 22, 592-605, 2008.
On the Autoreducibility of Random Sequences
by Ebert, Merkle, Vollmer SIJCOMP Vol 32, No 6, 2003. HAT PROBLEM: Simul, 2-colors, everyone passes or
guesses, at least 1 must not pass and get it right, nobody can get it wrong. Random, not adversary.
A New variation of the Hat guessing game By Ma, Sun, Yu.
A new variation of hat guessing games
by Tengyu Ma, Xiaoming Sun, Huacheng Yu. HAT PROBLEM: Simul, c-colors, everyone passes or
guesses, at least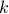 
must not pass and get it right, nobody can get it wrong. Random, not adversary.
Electronic Journal of Combinatorics.
Vol 24, Issue 1, 2017. HAT PROBLEM: Graph is cycle. Simul. Everyone says a color, 3 colors, Just need one to get it right.
Yet another hat game by Paterson, Stinson.
HAT PROBLEM: Line graph, 
colors, sequential voting, can pass, objective is at least one player gets it right
and nobody gets it wrong.
Covering codes for hats-on-a-line
by Aravamuthan and Lodha Hats on a line but with limited seeing or hearing
and perhaps a diferent order to yell out hat color. EJC.
Guessing games on triangle-free graphs
Cameron, Dang, Riis. HAT GAME is on a graph- simul, must get all right.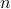 
people, colors. EJC.
Guessing Gameon Triangle-Free Graphs by Cameron, Dang, Riis
A construction for the hat problem on a directed graph
by Hod and Kzrzykowski. HAT GAME- 2 colors, on a directed graph, simul,
people can pass, but at least one has to get not pass and get it right.
Guessing number of odd cycles
by Atkins, Romback, Skerman.
HAT GAME: simul, on a graph, no passing, all must get it
correct, hats put on randomly, want high prob of success.
EJC 2017.
A Line of Sages
by Tanya Khovanova.
HAT GAME: 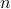hats,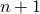 
colors, everyone gets a different color and everyone has to
say a different color. In a line.
Math Intelligence 2014
The Hat Game and Covering Codes
by Theo van Uem
HAT GAME: Simul, can pass, need to get at least 1 right, none wrong, prob putting hats on
BUT the prob are not 12-12.
The Three Hat Problem
by Brian Benson and Yang Want.
HAT GAME: Positive integers on the hats such that
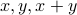. Players in turn either identify their number of pass.
Need to never be wrong an eventually someone is right.
arxiv 2007
General three and four player 2-color hat games
by Theo van Uem.
HAT GAME: Simul, can pass, need to get at least 1 right, none wrong, prob putting hats on
BUT the prob are diff for each player and known.
Asymetric Hat games with three players and three colors
by Theo van Uem.
HAT GAME: Simul, can pass, need to get at least 1 right, none wrong, prob putting hats on
BUT the prob are diff for each player and known.
Only covers the 3 player, 3 color case.
On Levine's infamous hat puzzle by Buhler et al.
New constructions and bounds for Winkler's hat game.
HAT PROBLEM- general graph, just need to have one person get it right.
Okay if others get it wrong, no passing, Simul
Finite dynamical Systems, Hat Games, and Coding Theory
by Maximilen Gadouleau
Applies Hat Games to dynamicals systems
On Hats and other Covers.
HAT GAME- Simul, some can pass, nobody can be wrong, random not adversary,
BUT with colors, not 2.
An Introduction to Infinite Hat Problems
by Christopher Hardin and Alan Taylor.
HAT GAME- infinite number of people, need to get all but a finite
number of them right. Needs AC.
The expressive power of voting polynomials
by Aspnes, Beigel, Furst, Rudich.
HAT GAME (not sure I would count it as such)- 0-1 value hats, randomized placement, want them to VOTE on the parity. Want over half to get it right.
Hat Problem on a Graph (PhD)}
by Marcin Krzywkowski.
HAT GAME- the people are on a variety of graphs.-