Project 1: 3D reconstruction

We were given the video of a scene from a lab. The goal was to reconstruct the 3D layout of the scene from 2 distant images/frames from the video. I adopted the following procedure to do the 3D reconstruction.

In order to get the 3D co-ordinates, we need to be able to get the projection matrix P. To get the projection matrix P,  we need to be able to find either the Fundamental Matrix F, or the essential matrix E. So, I first found the Fundamental matrix, the got the essential matrix, computed P using the fundamental matrix, and then get the 3D world points.

1. I took the two images and found the corresponding points manually. The corresponding points are needed to find F because of the property 

x'^TFx = 0;

2. I then used the 8-point algorithm to compute F. Basically, we just have to re-arrange the equations of the above to get Af = 0 where f is a 9x1 vector containing the elements of F. I then used Singular Value Decomposition to the value for the Fundamental matrix.

3. I then plotted the epipolar lines to see if the result was accurate. The following figure shows the epipolar lines. The cross-hairs in yellow are the points that were selected. Though it is not seen in the picture, I found that the epipolar lines meet in a small region rather than a single point. This is expected because of noise in the corresponding points. Also the F was not a rank 2 matrix. I found some methods to minimize the matrix. I idea was to assume F = SVD(UDV). and then set the (3,3) element of D to 0 and now get F. But when I did that, I found that the 3x3 element was already zero. So It was a pretty good result. 

I got the following value for F  =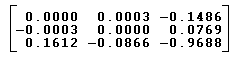

Fig 3: Epipolar lines on the image passing through the points clicked.

4. I then found the Essential Matrix using the Calibration toolbox available at the Caltech site.

I found that E =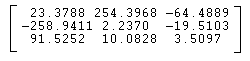

5. I then computed the projection matrix P, using the Fundamental matrix I had computed using point correspondences.

6. Finally I computed the 3D points using the idea that cross(x, PX) = 0. That is that cross product of image point x and Projection times the real world point is 0, to get the figure 4.