CMSC 311- Computer Organization

Fall 1995 - Assignment #1

Due (at the beginning of class) Thursday, September 14

  1. In class we saw that a NOR gate is functionally complete (it can be used to represent the other 7 gates). Show that NAND is functionally complete by showing how each of the other 7 gates can be constructed using one or more NAND gates.

  2. Given this circuit:

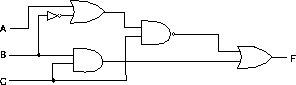
    Insert Circuit Here

    1. Write out the truth table.
    2. Write out the sum of products representation of F(A,B,C).
  3. Algebraically simply the following expressions to as few literals as possible:
    1. (x + y) (x + y')
    2. xyz + x'y + xyz'
    3. x + xz + yx + xyz + x'yz
    4. y(xz' + ((x' + z)y)')
  4. From Mano, problem 1-4.
  5. From Mano, problem 1-5.
  6. The implication function is one of the 16 possible functions of two Boolean variables. It is written x -> y, and is defined by x -> y = x' + y.
    1. Prove or disprove the associativity of this function (does (x -> y ) -> z = x -> (y -> z)).
    2. Prove or disprove the communtativity of this function (does x -> y = y -> x).
  7. From Mano, problem 1-7.
  8. Use Karnaugh maps to find a simplified sum of products representation of the following functions (you need to show the Karnaugh map to receive full credit).
    1. F(a,b,c) = (0,1,2,3)
    2. F(a,b,c) = abc' + ab'c' + a'bc' + a'bc
    3. F(a,b,c,d) = (1,2,4,5,7,8,10,11,13,14)
    4. F(a,b,c,d) = a'b'c + ad + bd' + cd' + ac' + a'b'