CMSC 417-F01 |
EXAM 2 SOLUTION |
Fall 2001 |
11111100
______________
10011 | 111011000100
10011
-----
11101
10011
-----
11100
10011
-----
11110
10011
-----
11010
10011
-----
10011
10011
-----
00000
00000
-----
00000
00000
-----
0000
It is acceptable because the remainder is 0000.
The data bit sequence is 11101100 (111011000100 minus last 4 bits).
GRADING:
Time At B, distance to D At C, distance to D
via node C via node B via node D
0.1 4* 6 2*
1.0 4* 6* 11
1.1 8* 6* 11
2.1 8* 10* 11
3.1 12* 10* 11
4.1 12* 14 11*
5.1 13* 14 11*
6.1 13* 15 11*
* indicates the minimum distance entry
Stable at time 6.1.
GRADING:
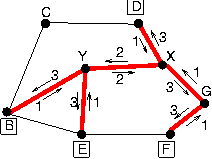
a.

b.
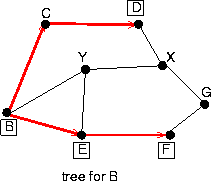
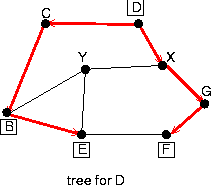
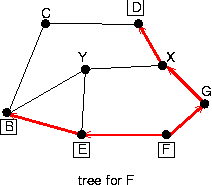
c.
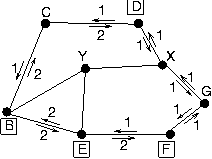
GRADING:
Below, * denotes multiplication and ** denotes exponentiation.
For slotted-ALOHA of N nodes, the throughput (as fraction of successful slots) is N*p*[(1-p)**(N-1)], where p is transmission probability. Thus maximum throughput is (1-p)**(N-1), which is achieved when p=1/N.
The 4-user group and even slots form a 4-node slotted-ALOHA system. Thus its max throughput is achieved when p=(1/4), and equals (1 - (1/4))**3, which equals (3/4)**3, which equals 27/64.
The 26-user group and odd slots form a 26-node slotted-ALOHA system. Thus its max throughput is achieved when p=(1/26), and equals (1 - (1/26))**25, which practially equals (1/e).
Thus the overall throughput is (1/2)[(27/64) + (1/e)]
GRADING: