About me
I am currently a 3rd-year PhD student at University of Maryland, College Park. My research interest lies in effective, efficient, reliable and robust (E2R2) algorithms for point cloud analysis. These requirements include but not limited to accuracy, robustness to noise, robustness to density variation, computation and memory efficient.
I believe my development will pave the path to point cloud foundation models. It will be a long journey, but I've already achieved a few milestones! Check my Point Cloud E2R2 Theories blog for a quick overview of my current developed theory and its future work!
I have the fortune to be advised by Prof. Yiannis Aloimonos and Dr. Cornelia Fermüller in the Perception and Robotics Group. I am also co-advised by Prof. Furong Huang. Before that, I worked as a research assistant for Prof. Jimmy Fung and Prof. Xingcheng Lu during my undergraduate for three years.
I received by Bachelor's degree in Mathematics and Economics & Computer Science at Hong Kong University of Science and Technology (HKUST) in 2021. I graduated with S.S. Chern (陈省身) class outstanding academic achievement in Mathematics (top 1%, awarded $30,000 HKD).
News and Highlights
| [2024.02] |
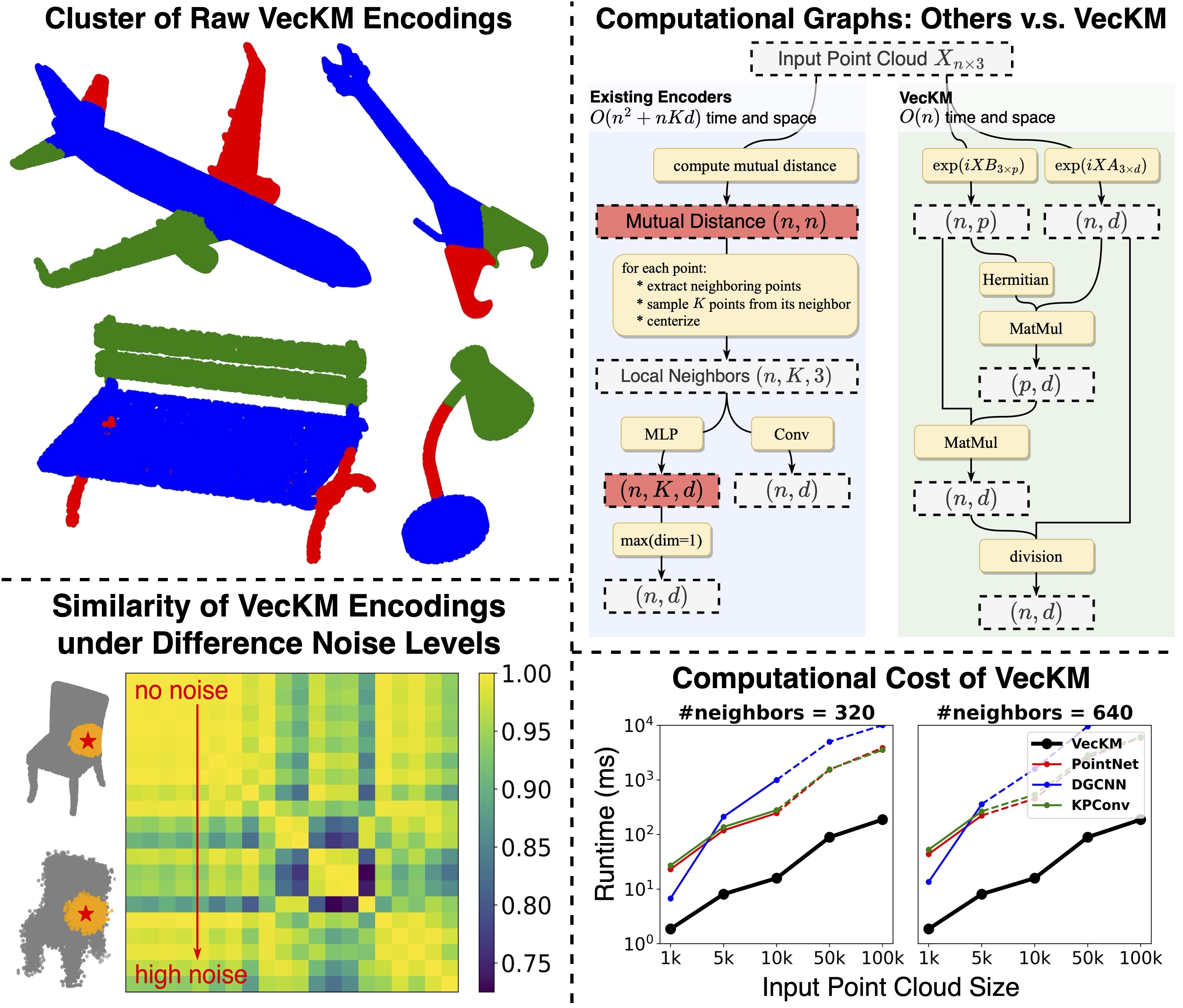
A new paper about efficient and robust local point cloud geometry encoder is under review.
|
| [2024.01] |
My first machine learning conference paper is accepted to ICLR2024! A zero-to-one step!
|
Selected Publications as a Research Assistant
As the second authors, I am responsible for data processing of > 100 GB, implementing machine learning architecture, generating the inference, and visualizing the outputs in the papers. These projects involve heavy data science components.
Xingcheng Lu, Dehao Yuan, Yiang Chen, Jimmy C.H. Fung
Environmental Pollution (I.F. 10.0) [Paper]
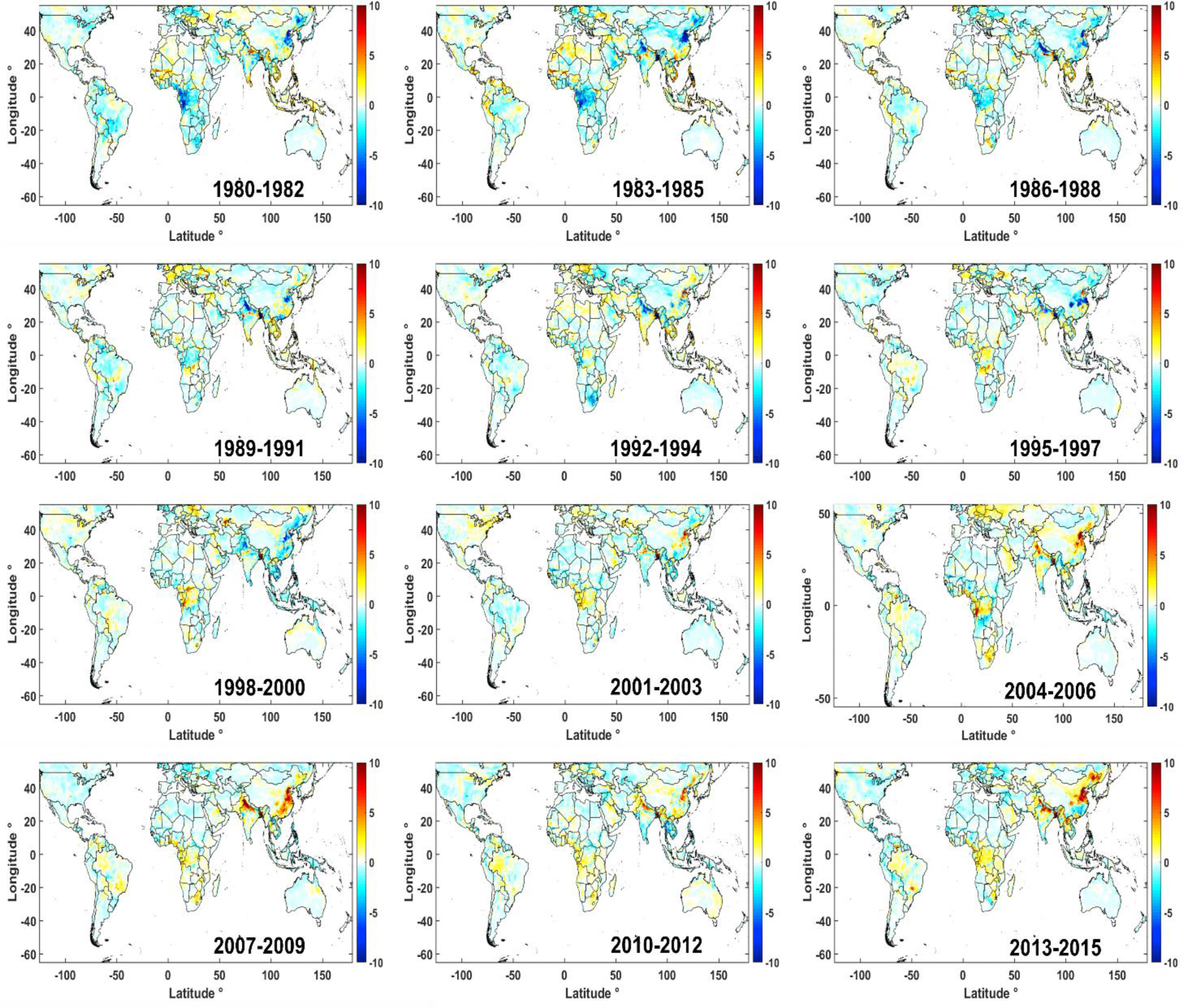
Description: We reveal the negative health impacts of PM2.5 pollution and its connection to urbanization and long-term meteorological changes. We reveal that urbanization tends to increase global PM2.5 levels and associated mortality, with urban residents being more vulnerable to adverse meteorological conditions. Machine learning analysis shows that meteorological influences on PM2.5-related health burdens have grown over time, emphasizing the need for climate mitigation efforts to address this issue.
Xingcheng Lu, Dehao Yuan, Yiang Chen, Jimmy C.H. Fung, Wenkai Li, and Alexis K.H. Lau
Environmental Science and Technology (I.F. 11.4) [Paper]
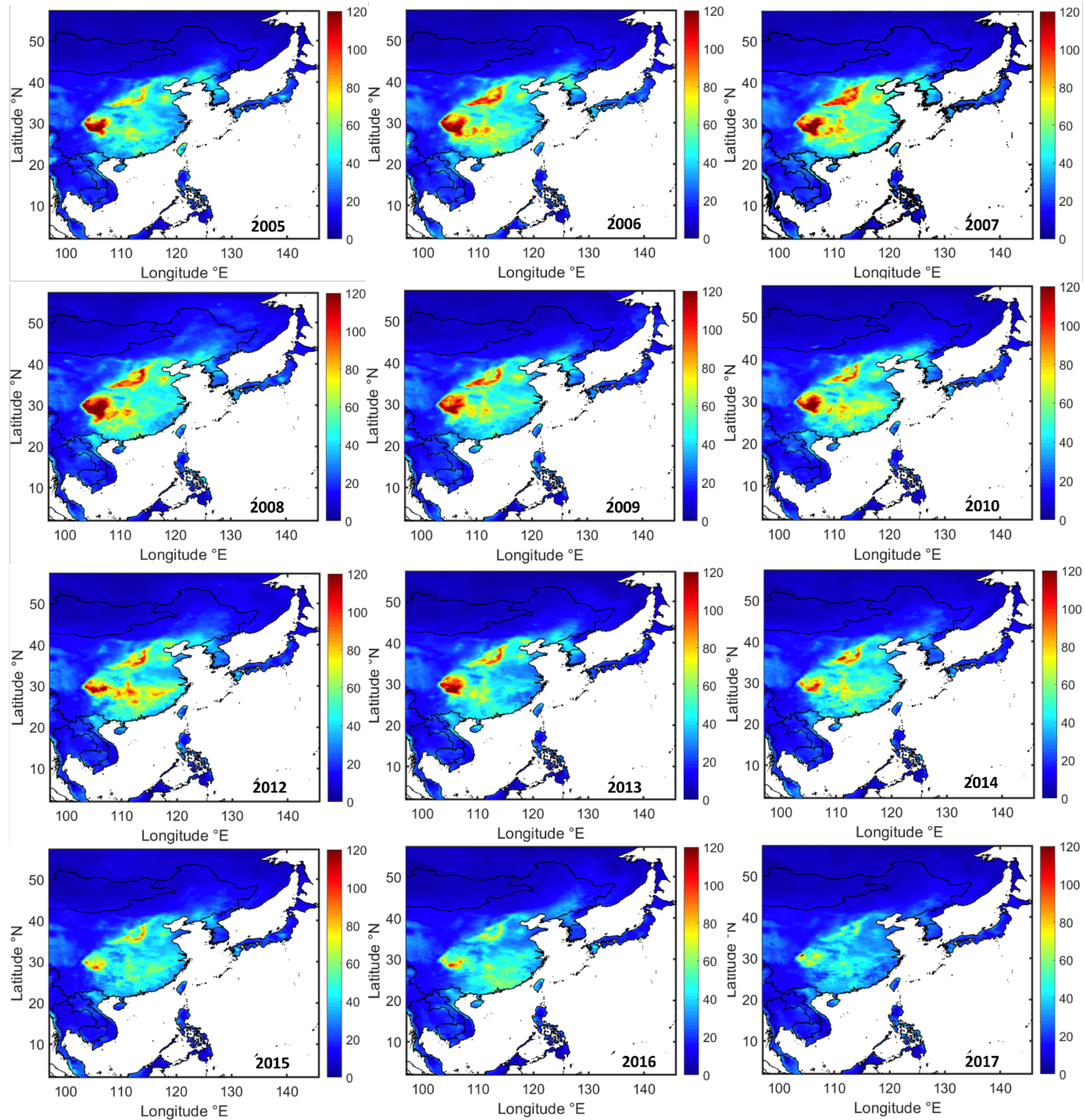
Description: We use an ensemble neural network to estimate the long-term wet deposition of harmful substances (nss-SO42– and NO3–) resulting from human emissions over East Asia. The model's accuracy is high, with R2 values of 0.90 for nss-SO42– and 0.85 for NO3–. We identify hotspots for these depositions in southwestern, central, and eastern China. Notably, we find that acidity in rainwater is shifting from sulfur to nitrogen dominance in most regions. Additionally, We reveal that some ecosystems, particularly freshwater bodies and grasslands, are experiencing wet depositions that exceed critical load thresholds, indicating a need for stricter, collaborative emission control measures in East Asia to protect these ecosystems.
Yiang Chen, Dehao Yuan, Wanying Chen, Mingyun Hu, Jimmy C.H. Fung, Haochen Sun, Xingcheng Lu
Chemosphere (I.F. 9.6) [Paper]
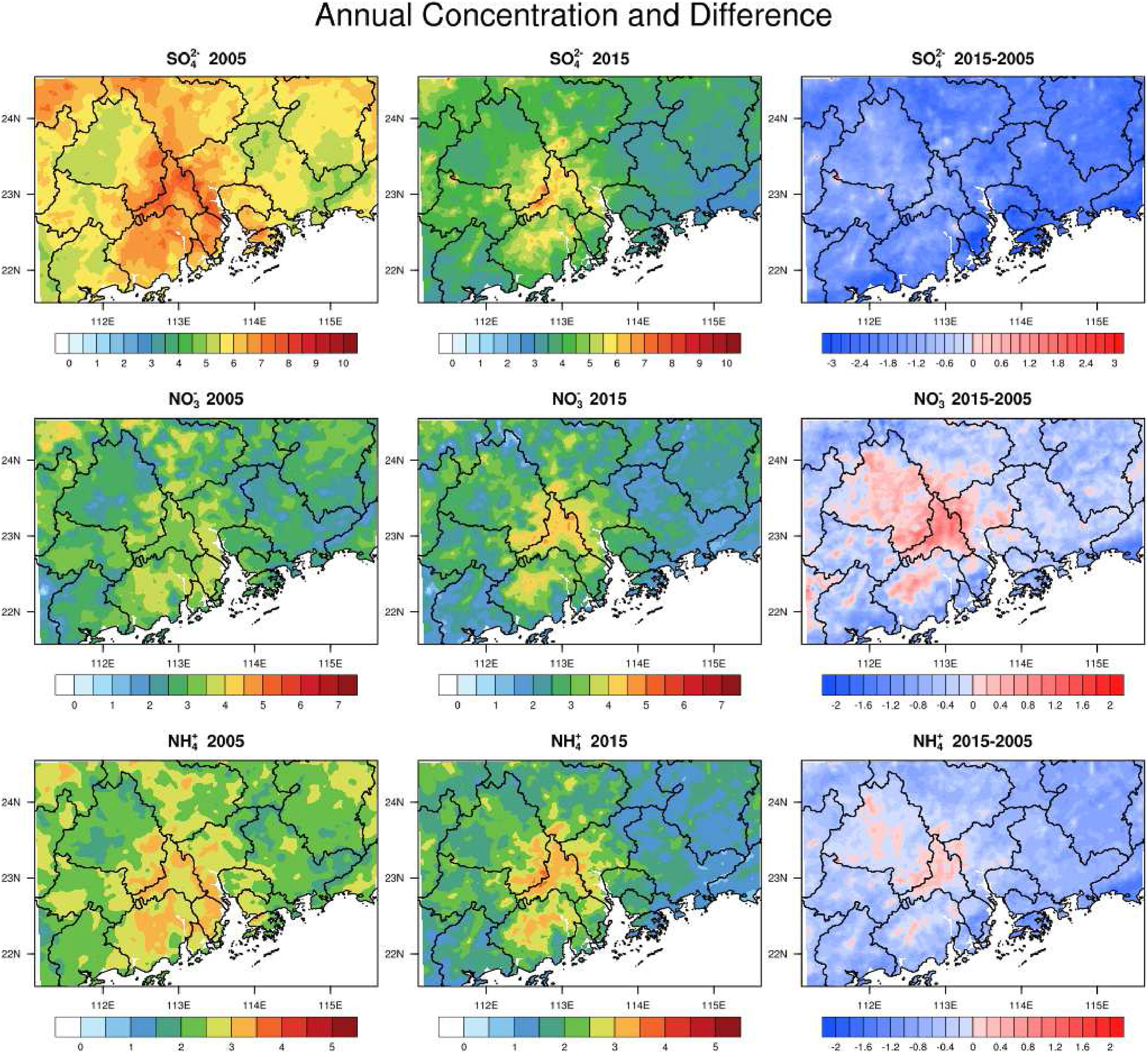
Description: We address the importance of understanding secondary inorganic aerosols in PM2.5 pollution. We use an ensemble neural network model combining numerical models and data to estimate aerosol concentrations in the Greater Bay Area in 2005 and 2015. The model outperforms traditional air quality models, showing decreasing concentrations of SO2-4, NO-3, and NH+4 from 2005 to 2015. Analysis reveals reduced sulfate formation due to emission controls, while increased ammonia availability leads to more sulfate neutralization. We underscore the need for controlling ammonia emissions to further reduce aerosol concentrations in the future.
My Course Notes
I enjoy learning mathematics and organize the lecture notes. Here are my lecture scribings using Notability, which help me build up very solid understanding on the materials.
Fundamental Courses
- MATH1023 Honor Calculus I
- MATH1024 Honor Calculus II
- MATH2023 Multivariable Calculus
- MATH2131 Honor Linear Algebra
Analysis
- MATH2033 Analysis I
- MATH2043 Honor Analysis I
- MATH3033 Analysis II
- MATH3043 Honor Analysis II
- MATH4023 Complex Analysis
- MATH4051 Theory of ODE
Statistics and Probability
- MATH2411 Statistics
- MATH2431 Honor Probability
- MATH3322 Matrix Computation
- MATH3423 Statistical Inference
- MATH3424 Regression Analysis
- MATH3425 Stochastic Process