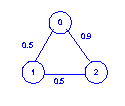
Figure 2: Sample network
You are the chief network designer for Web Reliable, yet another new ISP that will revolutionize the web as we know it. Web reliable promises to transform the current world-wide-wait into a usable functioning information infrastructure. Their claim is simple: Web reliable provides the most reliable network paths. How? Well, thats where you come in.... The marketing people got a bit carried away and have started a huge ad. campaign without all the technical problems being completely solved. The research lab has come up with a way to find out how reliable each network link in the Web reliable network is. Your job is to use that information and deliver on the Web reliable promise, i.e., find the most reliable paths.
The input to your program is a description of the Web reliable network
3 3 0 1 0.5 0 2 0.9 1 2 0.5The network described by the input file corresponds to the network shown in Figure 2.
The first line lists the total number of nodes in the network, and the total number of edges. Each remaining line consists of two node numbers n m (representing a edge between n and m) and the probability the edge may fail.
Edges are bi-directional: they are specified by a pair of nodes and a probability of failure. The probability of failure is a floating point number in the range (0,1]. Thus, the first line 0 1 0.5 means that there is a link between routers 0 and 1 with probability of link failure equal to 0.5.
The number of edges lines must be equal to the number of edges specified in the beginning. Also, the node identifiers must be in the range 0 .. (NUMNODES - 1).
You are guaranteed that there is at least one path from node 0 to every other node. There are no self loops (i.e. an edge starting and ending at the same node).
The output of your program is a set of paths and their associated success probabilities from node 0 in the following format:
From node 0 to node 1: Prob.(Success) = 0.50, Path: 0 -> 1 to node 2: Prob.(Success) = 0.25, Path: 0 -> 1 -> 2
Note that in this example, even though there was a direct link from 0 to 2, the most reliable path went through node 1.
In this example, the path to node 3 goes through node 1 (and not node 2) because {0, 1, 3} is ``lexicographically smaller'' than {0, 2, 3}. Stated differently, the algorithm could choose either 1 or 2 at node 0: it chose 1 since 1 ;SPMlt; 2.
Input:
4 4 0 1 0.5 0 2 0.5 1 3 0.5 2 3 0.5Output:
From node 0 to node 1: Prob.(Success) = 0.50, Path: 0 -> 1 to node 2: Prob.(Success) = 0.50, Path: 0 -> 2 to node 3: Prob.(Success) = 0.25, Path: 0 -> 1 -> 3
| Input 1 | Output 1 |
|---|---|
| Input 2 | Output 2 |
| Input 3 | Output 3 |