Quaternions are a generalization of the complex number system, developed by Sir William Hamilton in the mid 19th century. Today quaternions are used in computer graphics and robotics, since a quaternion naturally encodes a rotation in 3-space, and multiplication of quaternions corresponds to composition of rotations. For our purposes, a quaternion is defined to be a quadruple of numbers
where 
is of type double. Given two quaternions, q and
p, their sum, product, and negation are defined as follows:
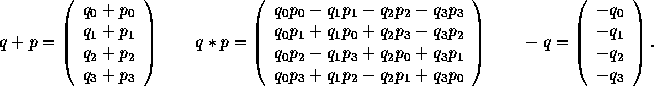
The objective of this problem is to design a simple calculator for quaternions. The calculator has 10 registers, numbered 0 through 9, each of which holds a single quaternion. Initially they are all set to zero. Your calculator will input a sequence of commands, each consisting of an operator followed by one or more arguments, and it will output the result of each operation.
Each line will contain a single character ``opcode'' followed by one or
more arguments, all separated by spaces. Here are the possible opcodes,
and their action. The values i, j, and k are integers in the
range 0 through 9 (inclusive) and the values are of type double.
You may assume that the input is in this format (e.g. you will not be
given any illegal opcodes).
With the exception of the `Q' opcode, each operation that is executed
outputs the result of the operation in the following format
, where i is the index of the register into
which the result was stored.
Input 1:
= 1 1 0 0 0 = 1 0 1 0 1 + 0 1 2 * 0 1 9 - 1 9 Q
Output 1:
[0] ( 1 1 0 0 ) [1] ( 1 0 1 0 ) [2] ( 2 1 1 0 ) [9] ( 1 1 1 1 ) [9] ( -1 0 -1 0 )
Input 2:
= 1 .5 0 0 0 = 1 -1 0 0 1 = 0 0 1 0 2 = 0 0 0 1 3 - 3 3 + 2 3 6 * 0 1 4 * 4 0 4 Q
Output 2:
[0] ( 1 0.5 0 0 ) [1] ( 1 -1 0 0 ) [2] ( 0 0 1 0 ) [3] ( 0 0 0 1 ) [3] ( 0 0 0 -1 ) [6] ( 0 0 1 -1 ) [4] ( 1.5 -0.5 0 0 ) [4] ( 1.75 0.25 0 0 )
| Input 1 | Output 1 |
|---|---|
| Input 2 | Output 2 |
| Input 3 | Output 3 |
| Input 4 | Output 4 |
| Input 5 | Output 5 |
| Input 6 | Output 6 |