Next: Comparing Trees Up: No Title Previous: Quaternion Calculator

The Spy's Escape Route

This problem involves computing shortest path subject to motion constraints, as is common in robotics applications.

A spy is trying to find her way home from her secret hangout to her home base. The streets of the city are laid out on a square grid. Some intersections cannot be visited, because they have surveillance cameras. She can only change directions when she comes to an intersection. To avoid detection, she intentionally avoids walking straight whenever possible. For example, if she enters an intersection from its south side, then she must leave by going either east, west or back south again, but she cannot continue straight north. The spy is allowed to visit the same intersection more than once.

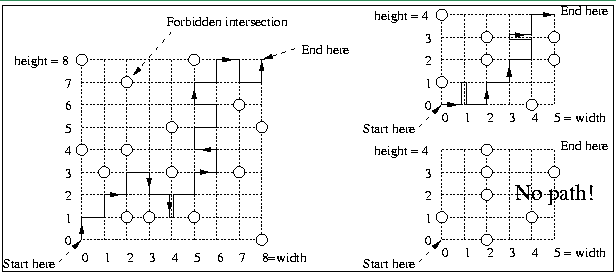
Write a program which determines whether the spy can make it home subject to these restrictions, and if so, outputs such a path. The figure below shows some possible situations. Notice that the path may backtrack at some points. In the situation in the lower right there is no path, because any path must go straight through the intersection at (2,1), and this is forbidden. The spy always starts in the lower left corner and goes to the upper right corner.

Input format

The first line of input contains two integers, giving the width w and height h of the grid. There are h+1 east-west streets with y-coordinates ranging from 0 to h, and there are w+1 north-south streets, with coordinates ranging from 0 to w. The remaining lines contain the integer x and y coordinates of the forbidden intersections. They are not given in any particular order. The list is terminated by a line containing only -1. The spy starts her walk in the lower-left corner (with coordinates (0,0)) and ends in the upper-right corner (with coordinates (w,h)). You may assume that w and h are each in the range from 0 to 100.

Output format

If there is no path from the start to end or if any such path would require walking straight through an intersection, then output ``no-path'' on a single line. Otherwise if there is a path, output ``path'' on one line. Each of the remaining lines of output contains the x and y coordinates (separated by spaces) of the intersections along the path, starting with (0,0) and ending with (w,h). The path does not need to be the shorest possible.

Example

The example below shows the input and output for the situations shown in the above figure on the right.

Input 1:

5 4
0 1
0 4
2 2
2 3
4 0
5 2
5 3
-1

Output 1:

path
0 0
1 0
1 1
1 0
2 0
2 1
3 1
3 2
4 2
4 3
3 3
4 3
4 4
5 4

Input 2:

5 4
0 1
2 0
2 2
2 3
2 4
4 1
5 3
-1

Output 2:

no-path

Test data used in judging

Input 1	Output 1
Input 2	Output 2
Input 3	Output 3
Input 4	Output 4
Input 5	Output 5
Input 6	Output 6
Input 7	Output 7

Our Solution

Next: Comparing Trees Up: No Title Previous: Quaternion Calculator