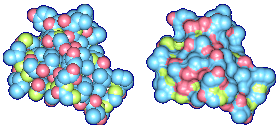
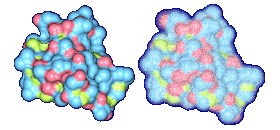
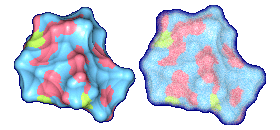
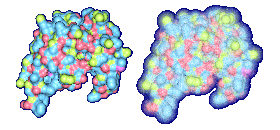
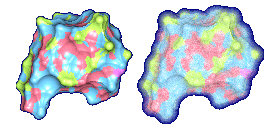
We propose a method to compute fuzzy molecular surfaces. We define two concepts for computing fuzzy molecular surfaces: (a) A p-probability sphere is defined for each atom as the smallest sphere that contains the center of that atom with a probability p. (b) An extended-radius p-probability sphere is defined for atom i as the smallest sphere that contains the atom i with a probability p. The Gaussian distribution is used for modeling the fuzziness of each atom, and a p-probability sphere is computed for each atom with a certain confidence level. The fuzzy molecular surface is computed efficiently from extended-radius p-probability spheres. We have implemented a program for visualizing three-dimensional molecular structures including the smooth molecular surface with fuzzy atoms using multi-layered transparent surfaces, where the surface of each layer has a different confidence level and the transparency associated with the confidence level.
The smooth molecular surface, first proposed by Richards in 1977, is defined as the surface which an external probe sphere touches when it is rolled over the spherical atoms of a molecule. The smooth molecular surface is useful for studying the structure and interactions of proteins, especially for testing the accessibility of a solvent into a molecule, for prediction of three-dimensional structures of biological macromolecules and assemblies, and for discriminating between different ways of docking molecules which can be used in drug design.
Many researchers have proposed methods to compute the smooth molecular surface, and they have assumed that each atom in a molecule has a certain rigid position. In real world, an atom in a molecule vibrates because of its thermal energy. Therefore, the smooth molecular surface will also vibrate. Also in protein structure determination, sometimes the positions of the atoms are uncertain. This information is useful and should be displayed with the rest of the molecule's visual attributes. In this research, we propose a method to compute the smooth molecular surface with atoms that are either vibrating or otherwise have uncertainty in their positions. The understanding of thermal motion and uncertainty provides a more informative molecular display and a better understanding of its structure and function.
In this research we propose a method for modeling fuzzy molecular surfaces and an algorithm for computing fuzzy molecular surfaces. The main contributions of this research are:
- We present a method to represent the different fuzziness on the molecular surface.
- We provide an efficient algorithm for computing and visualizing fuzzy molecular surfaces.
We have implemented a program for visualizing three-dimensional smooth molecular surface with and without atom vibrations and uncertainty. This program reads the information of each atom in a molecule such as geometric coordinates, atom type, and amino acid type, from a PDB file, then builds and visualizes a molecule. To express the fuzziness of the surface, the smooth molecular surface is visualized using multi-layered transparent surfaces, where the surface of each layer has a different confidence level and the transparency associated with the confidence level. To speed up the rendering time, less-detailed surfaces are used for the fuzzy surfaces so that smaller number of meshes can be used. Users can interactively change the maximum confidence level and the probe radius. The program is implemented on a Pentium4 1.5GHz PC with an NVIDIA Quadro2 Pro graphics card, using OpenGL Version 1.2.
Table 1 shows the times taken for computing and visualizing the molecular surfaces. We used seven layers for the multi-layered surfaces including the crisp molecular surface. We use less-detailed surfaces for fuzzy surfaces, so the number of triangles for the fuzzy surface versus the number of triangles for the crisp surface is a factor between 3 and 3.6 instead of 7. To compute the intermediate layers, we interpolate the crisp surface and the highest layer. The construction time for the fuzzy surface versus the construction time for the crisp surface is a factor between 2.8 and 3.2. The display time for the fuzzy surface is 3.7 to 4.1 times more than the display time for the crisp surface. This is more than what we would expect by just looking at the number of triangles. This is because the fuzzy layers use texture mapping and transparency which slow down their display.
Table 1. Running times with probe radius 1.4
Molecule Surface type Number of triangles Construction time (sec) Display time (sec) Crambin
(327 atoms)Crisp Surface 27,359 0.490 0.050 Fuzzy Surface 98,687 1.372 0.200 HIV Protease
(760 atoms)Crisp Surface 68,862 1.262 0.110 Fuzzy Surface 239,262 4.015 0.451 Mycobacterium tuberculosis
(1994 atoms)Crisp Surface 153,448 3.935 0.230 Fuzzy Surface 458,134 12.347 0.861
We have outlined an algorithm to compute and visualize a molecular surface from atoms with fuzzy positions using multi-layered surfaces. Using this algorithm, thermal motions and uncertainty of the center positions of atoms can be represented in molecular surfaces. This provides a more informative molecular display that presumably lead to a better understanding of protein structure and function. We have assumed that the fuzziness of an atom to be isotropic, but a molecular surface with more general anisotropic displacement parameters could be more useful. We plan to consider this in future.
- C. H. Lee and A. Varshney, Representing Thermal Vibrations and Uncertainty in Molecular Surfaces, SPIE Conference on Visualization and Data Analysis, San Jose, CA, January 2002
We would like to acknowledge the following sources:
This material is based upon work supported by the National Science Foundation under grants ACR-98-12572 and IIS-00-81847. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Web Accessibility