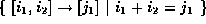


Next: 1.4 What are Presburger
Up: 1 Introduction
Previous: 1.2 What is the
An integer k-tuple is simply a point in 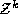 .
An integer tuple relation
is a mapping from tuples to tuples.
The tuple that is being mapped from is refered to as the input tuple and
the tuple that is being mapped to is refered to as the output tuple.
All the integer tuple relations we consider map from k-tuples to
.
An integer tuple relation
is a mapping from tuples to tuples.
The tuple that is being mapped from is refered to as the input tuple and
the tuple that is being mapped to is refered to as the output tuple.
All the integer tuple relations we consider map from k-tuples to 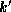 -tuples
for some fixed k and
-tuples
for some fixed k and 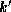 .
We refer to k and
.
We refer to k and 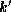 as the input and output arities respectively.
A integer tuple set
is a set of k-tuples, for some fixed k.
We'll often abbreviate integer tuple relations and integer tuple sets
as relations and sets respectively.
as the input and output arities respectively.
A integer tuple set
is a set of k-tuples, for some fixed k.
We'll often abbreviate integer tuple relations and integer tuple sets
as relations and sets respectively.
The sets and relations that we use may be infinite or may depend on the values
of other variables, so it is generally not possible to describe them simply by
enumerating their tuples or pairs of tuples.
Instead, we introduce variables that correspond to each of the positions in
the input and output or set tuples and construct a formula that has
these and other variables as free variables.
These variables are refered to as input, output or set variables as appropriate.
For example, we would represent the set of all even numbers as:
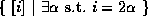 In this case we introduce a single set variable because we are describing a
set of 1-tuples.
The formula in this case is
In this case we introduce a single set variable because we are describing a
set of 1-tuples.
The formula in this case is 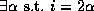 ,
note that i is the only free variable in this formula.
If we wanted to represent the set of all positive even numbers less than n
we would use:
,
note that i is the only free variable in this formula.
If we wanted to represent the set of all positive even numbers less than n
we would use:
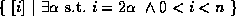 We refer to variables such as n as symbolic or global variables.
They are global in the sense that can be used in more than one relation
and they represent the same value in all relations.
This becomes important when we apply relational operations that combine
variables and constraints from different relations.
As another example,
to represent the relation corresponding to integer addition we would use:
We refer to variables such as n as symbolic or global variables.
They are global in the sense that can be used in more than one relation
and they represent the same value in all relations.
This becomes important when we apply relational operations that combine
variables and constraints from different relations.
As another example,
to represent the relation corresponding to integer addition we would use:
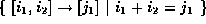
The Omega library can represent relations and sets that can be described by
Presburger formulas (possibly with limited uses of
uninterpreted function symbols).



Next: 1.4 What are Presburger
Up: 1 Introduction
Previous: 1.2 What is the
omega@cs.umd.edu
Web Accessibility
 .
An integer tuple relation
is a mapping from tuples to tuples.
The tuple that is being mapped from is refered to as the input tuple and
the tuple that is being mapped to is refered to as the output tuple.
All the integer tuple relations we consider map from k-tuples to
.
An integer tuple relation
is a mapping from tuples to tuples.
The tuple that is being mapped from is refered to as the input tuple and
the tuple that is being mapped to is refered to as the output tuple.
All the integer tuple relations we consider map from k-tuples to 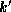 -tuples
for some fixed k and
-tuples
for some fixed k and 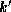 .
We refer to k and
.
We refer to k and 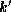 as the input and output arities respectively.
A integer tuple set
is a set of k-tuples, for some fixed k.
We'll often abbreviate integer tuple relations and integer tuple sets
as relations and sets respectively.
as the input and output arities respectively.
A integer tuple set
is a set of k-tuples, for some fixed k.
We'll often abbreviate integer tuple relations and integer tuple sets
as relations and sets respectively.
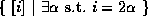 In this case we introduce a single set variable because we are describing a
set of 1-tuples.
The formula in this case is
In this case we introduce a single set variable because we are describing a
set of 1-tuples.
The formula in this case is 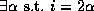 ,
note that i is the only free variable in this formula.
If we wanted to represent the set of all positive even numbers less than n
we would use:
,
note that i is the only free variable in this formula.
If we wanted to represent the set of all positive even numbers less than n
we would use:
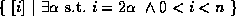 We refer to variables such as n as symbolic or global variables.
They are global in the sense that can be used in more than one relation
and they represent the same value in all relations.
This becomes important when we apply relational operations that combine
variables and constraints from different relations.
As another example,
to represent the relation corresponding to integer addition we would use:
We refer to variables such as n as symbolic or global variables.
They are global in the sense that can be used in more than one relation
and they represent the same value in all relations.
This becomes important when we apply relational operations that combine
variables and constraints from different relations.
As another example,
to represent the relation corresponding to integer addition we would use: