


Next: 1.5 What are uninterpreted
Up: 1 Introduction
Previous: 1.3 What are tuple
Presburger formulas [KK67] are those formulas that can be constructed
by combining affine constraints on integer variables with the logical operations
 ,
, 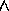 and
and 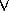 , and the quantifiers
, and the quantifiers 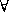 and
and 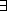 .
The affine constraints can be either equality constraints or inequality
constraints (abbreviated as EQs and GEQs respectively).
For example, the formulas in the previous section are Presburger formulas.
There are a number of algorithms for testing the satisfiability of arbitrary
Presburger formulas [KK67,Coo72,PW93].
The best known upper bound on the performance of an algorithm for
verifying Presburger formulas is
.
The affine constraints can be either equality constraints or inequality
constraints (abbreviated as EQs and GEQs respectively).
For example, the formulas in the previous section are Presburger formulas.
There are a number of algorithms for testing the satisfiability of arbitrary
Presburger formulas [KK67,Coo72,PW93].
The best known upper bound on the performance of an algorithm for
verifying Presburger formulas is 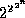 [Opp78],
and we have no reason to believe that our method will provide better
worst-case performance.
However, our method may be more efficient for many simple cases that arise in
our applications.
[Opp78],
and we have no reason to believe that our method will provide better
worst-case performance.
However, our method may be more efficient for many simple cases that arise in
our applications.
omega@cs.umd.edu
Web Accessibility
 ,
, 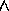 and
and 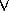 , and the quantifiers
, and the quantifiers 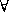 and
and 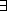 .
The affine constraints can be either equality constraints or inequality
constraints (abbreviated as EQs and GEQs respectively).
For example, the formulas in the previous section are Presburger formulas.
There are a number of algorithms for testing the satisfiability of arbitrary
Presburger formulas [KK67,Coo72,PW93].
The best known upper bound on the performance of an algorithm for
verifying Presburger formulas is
.
The affine constraints can be either equality constraints or inequality
constraints (abbreviated as EQs and GEQs respectively).
For example, the formulas in the previous section are Presburger formulas.
There are a number of algorithms for testing the satisfiability of arbitrary
Presburger formulas [KK67,Coo72,PW93].
The best known upper bound on the performance of an algorithm for
verifying Presburger formulas is 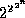 [Opp78],
and we have no reason to believe that our method will provide better
worst-case performance.
However, our method may be more efficient for many simple cases that arise in
our applications.
[Opp78],
and we have no reason to believe that our method will provide better
worst-case performance.
However, our method may be more efficient for many simple cases that arise in
our applications.