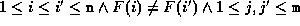Presburger arithmetic can be extended to allow uninterpreted
function symbols
.
Formulas in this extended class may contain
terms representing the application of a function
to a list of argument terms.
For example, the following extended presburger formula contains an uninterpreted
function symbol F:
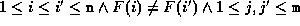The functions are termed ``uninterpreted''
because the only thing we know about them is that they are functions:
two applications of a function to the same arguments will produce the
same value.
Applications of function symbols can be used to represent values that vary with the values of certain other variables. For example, when we perform dependence analysis with the Omega Library, we would use a scalar global variables to represent the value of a symbolic constant in the program, and a function of arity 2 to represent the values taken on by a non-linear expression nested in two loops (see [PW94] for a more detailed discussion of, and examples of, the use of function symbols to represent non-linear terms).
Downey ([Dow72]) proved that full Presburger arithmetic with uninterpreted function symbols is undecidable. We therefore restrict our attention to a subclass of the general problem, and produce approximations whenever a formula is outside of the subclass. Whenever an approximation is produced, it is marked as either an upper bound or lower bound as appropriate. We currently restrict our attention to formulas in which all function symbols are free, and functions are only applied to a prefix of the input or output tuple. For example, a binary function could be applied to the first two input or the first two output variables of a Relation (or the first two variables of a set's tuple).