Notes

1 August 27, 2018

First lecture is postponed until Wednesday.

2 August 29, 2018

Audio and video capture from today’s class is available here.

3 August 31, 2018

Audio and video capture from today’s class is available here.

4 September 5, 2018

Audio and video capture from today’s class is available here.

Here is the code I asked you to explore for Friday:

(define (tax i)

(cond [(and (> i 0) (<= i 100000)) (* 0.1 i)]

[(and (> i 100001) (<= i 1000000)) (* 0.2 i)]

[(>= i 1000001) (* 0.02 i)]))

(tax 100)

(tax 2000000)

5 September 7, 2018

Audio and video capture from today’s class is available here.

6 September 10, 2018

Audio and video capture from today’s class is available here.

7 September 12, 2018

Audio and video capture from today’s class is available here.

8 September 14, 2018

Audio and video capture from today’s class is available here.

Here is the code I presented in class:

;; Authors: dvanhorn

;; Purpose: Construct greetings for CMNS Development office letters

;; -----------------------------------------------------------------------------

;; Data Definitions

;; A Name is a non-empty String

;; interp: string represents full name of person

(define BH "Bob Harper")

(define AAA... (replicate 100 "AAA")) ; a really long name

;; name-template : Name -> ??

(define (name-template n)

(... n ...))

;; -----------------------------------------------------------------------------

;; Defined Constants

(define NAME-MAX-LENGTH 100) ; [10,100]

;; -----------------------------------------------------------------------------

;; Functions

;; greeting : Name -> String

;; Create the greeting for a donor letter

(check-expect (greeting BH) "Dear Bob Harper,")

(check-expect (greeting AAA...) "Dear A.,")

(define (greeting n)

(string-append "Dear " (name-truncate n) ","))

;; name-truncate : Name -> String

;; Truncate long names to first letter and ".", or leave as is.

(check-expect (name-truncate BH) "Bob Harper")

(check-expect (name-truncate AAA...) "A.")

(define (name-truncate n)

(cond [(too-long? n) (string-append (string-ith n 0) ".")]

[else n]))

;; too-long? : Name -> Boolean

;; Is the given name too long to fit on a page?

(check-expect (too-long? BH) #false)

(check-expect (too-long? AAA...) #true)

(define (too-long? n)

(> (string-length n) NAME-MAX-LENGTH))

9 September 17, 2018

Audio and video capture from today’s class is available here.

10 September 19, 2018

Audio and video capture from today’s class is available here.

11 September 21, 2018

Audio and video capture from today’s class is available here.

12 Midterm 1 Drills

Here are some drill questions to practice for the first midterm. These only cover topics we’ve covered so far in class, but more topics will be on the midterm. I will post relevant drill problems as appropriate.

12.1 Simple computations

Determine what the following programs evaluate to:

• (- (sqr 5))

• (modulo 12 5)

• (+ (/ 4 3) 1)

• (string-append "Hello" "World")

• (string-append "" "Fred")

• (substring "manslaughter" 4)

• (above (circle 10 "outline" "black") (square 5 "outline" "black"))

• (substring (string-append "te" "am") 1 3)

• (+ (posn-x (make-posn 3 4)) (posn-x (make-posn 10 2)))

• (define-struct name (first last))

  (make-name "James" "Bond")

• (define first-name "James")

  (define last-name "Bond")

  (string-append last-name ", " first-name " " last-name)

• (define x 3)

  (define y 4)

  (sqrt (+ (sqr x) (sqr y)))

• (define-struct name (first last))

  (define ms (make-name "Michael" "Scott"))

  (define sm (make-name (name-last ms) (name-first ms)))

  (name-last sm)

• (define (f x)

  (/ (sqr x) 2))

  (+ (f 5) (f 2))

• (define (g y)

  (cond [(<= (string-length y) 4) 3.25]

  [else "yellow"]))

  (g "pie")

12.2 Stepping through computations

Write out each step of computation. At each step, underline the expression being simplified. Label each step as being "arithmetic" (meaning any built-in operation), "conditional", "plug" (for plugging in an argument for a function parameter), or "constant" for replacing a constant with its value.

• (+ (sqr 5) (add1 2))

• (define Q 2)

  (define (h z)

  (+ (* z 5) Q))

  (cond [(= (h 1) 7) (add1 9)]

  [(= (h 2) 12) 4])

• (define (hi name)

  (string-append "Hi " name "!"))

  (hi (substring "DVH" 0 1))

• (define s (make-posn "GOOG" 99))

  (cond [(< 100 (posn-y s)) "sell"]

  [(> 100 (posn-y s)) "buy"]

  [else "nada"])

12.3 Classifying errors

Classify the following programs as having a syntax error, a run-time error, logical error, or having no errors.

• (define (f x) (expt 2 x))

  (check-expect (f 4))

• (string-append "Hi " (substring "DVH" 1 4))

• ; dist : Number Number -> Number

  ; Compute distance to origin of (x,y)

  (define (dist x y)

  (sqrt (+ (sqr x) (sqr x))))

  (dist 3 4)

• (define h z (+ z (sqr z)))

12.4 Stubs, Templates

Assume the following data definitions:

; A Name is a (make-name String String)

(define-struct name (first last))

; A Shape is one of:

; - (make-rect Integer Integer)

; - (make-circ Integer)

(define-struct rect (width height))

(define-struct circ (radius))

; A Drawing is one of:

; - Shape

; - (make-posn Shape Shape)

; A Price is one of

; - [0,99)

; - [99,999)

; A Move is one:

; - "N"

; - "E"

; - "W"

; - "S"

; - "NE"

; - "NW"

; - "SE"

; - "SW"

; A MaybeMove is one of:

; - Move

; - #false

; A Niner is a 9

; A Biz is one of:

; - "a"

; - 7

; - #true

; - (make-posn 9 9)

Write templates for each of these data definitions.

Write stubs for each of these signatures.

; greeting : Name -> String

; cheap? : Price -> Boolean

; next-move : Move -> MaybeMove

; area : Drawing -> Number

; sign : Shape -> Name

; inc : Number -> Niner

; choose : Move Move -> Move

; cost : Drawing -> Price

; cap : Shape String Image -> Biz

; same-price? : Price Price -> Boolean

; bribe : Price -> Name

; change-last : Name String -> Name

; dot : String Integer -> String

; cross : String Move -> Shape

; all-on? : Shape Shape Shape Shape -> Boolean

; flip : Move -> Move

; rotate : Image MaybeMove -> Shape

12.5 Designing functions

; A Name is a (make-name String String)

; Interp: a person's full (first and last) name.

; Both strings must contain at least one letter.

(define-struct name (first last))

Design a function that creates a opening phrase of a letter. For example, given the full name David Van Horn, produces "Dear David,".

Design a function that is given two full names and a first name. It should produce a new name using the given first name and a hyphenated combination of the last names of the two full names. For example, given full names Ed Tobin, Laura Hochstadt, and the first name Sam, it should produce the full name Sam Tobin-Hochstadt.

Design a function that is given a full name and produces a “private” version of the name that abbreviates the last name to the first letter and a period. So for example, given the full name David Van Horn, then the full name David V. would be the produced.

Design a function that is given two full names and determines whether the two people have the same first name.

; A Dir is one of:

; - "N"

; - "E"

; - "W"

; - "S"

; Interp: North, East, West, and South.

Design a function that computes the opposite of a given direction.

Design a function that determines if two directions are the same.

Design a function that determines if two directions are opposites of each other.

Design a function that computes a right turn from the given direction.

Design a function that given a direction computes a name (as in a Name) like this: given "S" it should compute "South Southwest" where South is the first name and Southwest is the last name. North should give you North Northwest, etc.

; A Coord is a (make-posn Integer Integer)

; Interp: a Cartesian coordinate

Design a function that takes two coordinates and computes a coordinate representing their sum, e.g. (x1,y1) + (x2,y2) = (x1+x2,y1+y2).

Design a function that, given a coordinate (x,y), computes the area of the triangle formed by (0,0), (x,0), and (x,y). Recall the area of a triangle is 1/2 * base * height.

Design a function that, given a coordinate (x,y), computes the perimeter of the triangle formed by (0,0), (x,0), (x,y).

Design a function that reflects a coordinate over the x-axis, e.g. (5,3) becomes (5,-3).

12.6 Solutions

Here are videos going through solutions to each part of the drill problems:

• Simple computations

• Stepping through computations

• Classifying errors

• Templates

• Stubs

• Designing Name functions

• Designing Dir functions : the video file was corrupted

• Designing Coord functions

13 September 24, 2018

Audio and video capture from today’s class is available here.

14 September 26, 2018

Audio and video capture from today’s class is available here.

15 September 28, 2018

Audio and video capture from today’s class is available here.

16 October 3, 2018

Audio and video capture from today’s class is available here.

17 October 5, 2018

Audio and video capture from today’s class is available here.

18 October 8, 2018

Audio and video capture from today’s class is available here.

19 October 10, 2018

Audio and video capture from today’s class is available here.

20 October 12, 2018

Audio and video capture from today’s class is available here.

21 October 15, 2018

Audio and video capture from today’s class is available here.

22 October 17, 2018

Audio and video capture from today’s class is available here.

23 Midterm 2 Drills

Here are some drill problems. (Solutions: drill-soln.rkt.)

Keep in mind that any topic from midterm 1 could show up again on midterm 2 so it may be worth revisiting older drill problems and the practice midterm 1.

23.1 Programming with functions

Design and abstraction called andf from the following two functions:

; even-pos? : Number -> Boolean

; Is the number even and positive?

(check-expect (even-pos? 4) #true)

(check-expect (even-pos? 3) #false)

(check-expect (even-pos? -1) #false)

(define (even-pos? n)

(and (even? n) (positive? n)))

; neg-odd? : Number -> Boolean

; Is the number negative and odd?

(check-expect (neg-odd? 4) #false)

(check-expect (neg-odd? 3) #false)

(check-expect (neg-odd? -1) #true)

(define (neg-odd? n)

(and (negative? n) (odd? n)))

Be sure to give andf the most general parametric signature that is valid.

Use your abstraction to define the following function (you may find string-alphabetic? and string-lower-case? helpful):

; string-lower-alpha? : String -> Boolean

; Is the string made up of lower case, alphabetic letters?

(check-expect (string-lower-alpha? "ABC") #false)

(check-expect (string-lower-alpha? "a2c") #false)

(check-expect (string-lower-alpha? "abc") #true)

(define (string-lower-alpha? s) ...)

Using only andf, >, even?, and lambda expressions, write an expression that produces a predicate on numbers that will produce true when applied to even numbers greater than 5.

23.2 Signatures

Provide the most general valid signature for the following functions.

(define (lengths xs)

(map length xs))

(define (total-length xs)

(foldr (λ (x t) (+ (length x) t)) 0 xs))

(define (map-f-zero lof)

(map (λ (f) (f 0)) lof))

23.3 Using list abstractions

Re-define the following functions in terms of list abstraction functions where appropriate. (Signatures and purpose statements intentionally omitted):

(check-expect (rev-append (list "there" "hi")) "hithere")

(define (rev-append los)

(cond [(empty? los) ""]

[(cons? los)

(string-append (rev-append (rest los)) (first los))]))

(check-expect (posns-at-x (list 1 2 3) 7)

(list (make-posn 7 1) (make-posn 7 2) (make-posn 7 3)))

(define (posns-at-x ys x)

(cond [(empty? ys) '()]

[(cons? ys)

(cons (make-posn x (first ys))

(posns-at-x (rest ys) x))]))

(check-expect (dist (make-posn 0 0) (make-posn 3 4)) 5)

(define (dist p q)

(sqrt (+ (sqr (- (posn-x p)

(posn-x q)))

(sqr (- (posn-y p)

(posn-y q))))))

(check-expect (close-by (make-posn 0 0) (list (make-posn 3 4) (make-posn 8 8)) 6)

(list (make-posn 3 4)))

(define (close-by p lop d)

(cond [(empty? lop) '()]

[(cons? lop)

(cond [(<= (dist p (first lop)) d)

(cons (first lop)

(close-by p (rest lop) d))]

[else

(close-by p (rest lop) d)])]))

(check-expect (draw-on (list (make-posn 50 50)))

(place-image (circle 10 "solid" "red") 50 50 (empty-scene 100 100)))

(define (draw-on lop)

(cond [(empty? lop) (empty-scene 100 100)]

[(cons? lop)

(place-image (circle 10 "solid" "red")

(posn-x (first lop))

(posn-y (first lop))

(draw-on (rest lop)))]))

23.4 Designing functions

Design a function that computes the “dot product” of two equal length lists of numbers. The dot product is the sum of the product of each corresponding elements in the lists. For example, the dot product of (list 1 2 3) and (list 4 5 6) is (+ (* 1 4) (* 2 5) (* 3 6)).

Notice that the outer product of a list of length N and of length M is a list of N lists of M numbers, with the exception that if M or N is 0, the result is an empty list.

Design an abstraction function for “outer-product-like" computations of any kind. Redefine your two outerproduct functions in terms of it.

Design a function append-to-each that consumes a string s and a list of string los and produces a list of strings like los but with s appended to the front of each element.

Design a function append-all that consumes two list of strings los1 and los2 and produces a list of strings that appends each element of los1 to all of the elements in los2. For example, (append-all (list "a" "b") (list "c" "d")) should produce (list "ac" "ad" "bc" "bd").

24 October 19, 2018

Audio and video capture from today’s class is available here.

25 October 22, 2018

Audio and video capture from today’s class is available here.

26 October 24, 2018

Audio and video capture from today’s class is available here.

27 October 26, 2018

Audio and video capture from today’s class is available here.

28 October 29, 2018

Audio and video capture from today’s class is available here.

29 October 31, 2018

Audio and video capture from today’s class is available here.

30 November 2, 2018

Audio and video capture from today’s class is available here.

31 November 7, 2018

Audio and video capture from today’s class is available here.

32 November 12, 2018

Audio and video capture from today’s class is available here.

33 November 14, 2018

Audio and video capture from today’s class is available here.

34 November 16, 2018

Audio and video capture from today’s class is available here.

35 November 19, 2018

Audio and video capture from today’s class is available here.

36 November 26, 2018

Audio and video capture from today’s class is available here.

37 November 28, 2018

Audio and video capture from today’s class is available here.

38 Final Exam Drills

The final exam is cumulative, so you should review Midterm 1 Drills and Midterm 2 Drills. The following drills only cover material introduced since the second midterm.

Solutions: drill-final-exam-soln.rkt.

38.1 Designing with accumulators

Here is a design of the factorial function using structural recursion on natural numnbers:

; factorial : Natural -> Natural

; Compute n!

(check-expect (factorial 5) 120)

(define (factorial n)

(cond [(zero? n) 1]

[else

(* n (factorial (sub1 n)))]))

Design a variant of factorial that uses structural recursion on n with an accumulator that represents the factorial of all the numbers seen so far.

Here is a design of the largest function that uses structural recursion on a non-empty list of (real) numbers to compute the largest number in the list:

; largest : [NEListof Real] -> Real

; Finds largest element in given non-empty list

(check-expect (largest (list 7)) 7)

(check-expect (largest (list 2 9 7)) 9)

(define (largest ns)

(cond [(empty? (rest ns)) (first ns)]

[else

(max (first xs)

(largest (rest xs)))]))

Design a variant of largest that uses structural recursion on ns with an accumulator that represents the largest element of the list seen so far.

Here is a design of the prod function that computes the product of a list of numbers:

; prod : [Listof Number] -> Number

; Compute the product of the list

(check-expect (prod '()) 1)

(check-expect (prod (list 1 2 3 4 5)) 120)

(define (prod xs)

(cond [(empty? xs) 1]

[(cons? xs)

(* (first xs)

(prod (rest xs)))]))

Here is a design of sum:

; sum : [Listof Number] -> Number

; Compute the sum of the list

(check-expect (sum '()) 0)

(check-expect (sum (list 1 2 3 4 5)) 15)

(define (sum xs)

(cond [(empty? xs) 0]

[(cons? xs)

(+ (first xs)

(sum (rest xs)))]))

Give alternative designs that use an accumulator to represent the product (resp. sum) of the numbers seen so far.

Based on your accumulator variant of prod and sum, design an abstraction of these two functions. Give it the most general signature you can. Reformulate your accumulator-based prod and sum functions in terms of this abstraction.

What does the abstraction remind you of?

Can you use your abstraction to reformulate largest?

Here is the design of a function called minf that consumes a function producing real numnbers and a non-empty list of input elements and finds the (earliest) element in the list that minimizes the output of the function:

; minf : [X] [X -> Real] [NEListof X] -> X

; Find the earliest element that minimizes f.

(check-expect (minf sqr (list -4 2 8)) 2)

(check-expect (minf sqr (list -4 -2 8 2)) -2)

(define (minf f xs)

(cond [(empty? (rest xs)) (first xs)]

[else

(local [(define x1 (first xs))

(define y1 (f x1))

(define xn (minf f (rest xs)))

(define yn (f xn))]

(if (<= y1 yn) x1 xn))]))

The observant reader will notice that function f is called 2 × (n-1) times (where n is the length of the list). Using an accumulator-based design, you can do better, calling the function at most n times. The trick is that you will need two accumulators: the minimizing element seen so far and the result of applying the function to that minimizing element; also note that you start these values off by using the first element of the list (which is guaranteed to exist).

Design a 2-accumulator-based version of minf and argue why it only calls f at most n times.

38.2 Generative recursion

Suppose we have a data definition for "ascening strings," i.e. strings that consist of letters that must appear in alpahabetic order in the string. For example, "aabcz" and "bdrtu" are ascending, but "efarw" is not.

; An AscString is a String

; where (explode s) is sorted by string<?

Design a function that is given an AscString and a 1String and determines if the given letter occurs in the string. It should use generative recursion to be more efficient than scanning the list. (You should not use string-contains?.)

38.3 Invariants

A Quad Tree is an important data structure for representing a set of spatial coordinates, for example a set of GPS locations, and supporting very efficient queries about whether a given point is in the set of locations or not.

The idea is to represent a set of points using a tree. Each node in the tree contains a point and four subtrees. The four subtrees have an important invariant: one holds all the points that are to the Northwest of the point in the node, another holds the points to the Northeast, another the Southeast, and another the Southwest.

Here is a data definition for quad trees:

; A QT (Quad Tree) is one of:

; - #false

; - (make-quad Posn QT QT QT QT)

(define-struct quad (pt ne nw se sw))

; Interp: a set of positions, #false represents an empty set

; Invariant:

;  - all points in ne are north (y is smaller) & east (x is larger) of pt

;  - all points in nw are north (y is smaller) & west (x is smaller) of pt

;  - all points in se are south (y is larger) & east (x is larger) of pt

;  - all points in sw are south (y is larger) & west (x is larger) of pt

(Note this uses the convention of graphics coordinates in which the y-axis grows downward.)

Define the following function, taking advantage of this invariant to compute the answer efficiently:

; contains? : Posn QT -> Boolean

; Is the given position in the set?

38.4 Graphs

When we studied graphs we used the follow data representation for graphs:

; A Graph is [Listof (cons String [Listof String])]

; Interp: a graph is a list of nodes and neighbors reachable from the node

So a graph such as this:

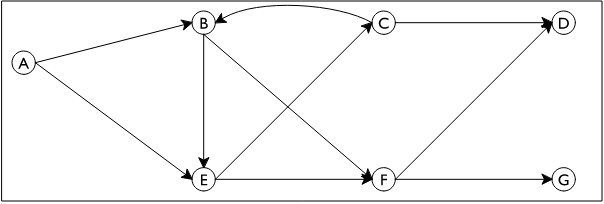
is represented as:

(define G

(list (list "A" "B" "E")

(list "B" "E" "F")

(list "C" "D" "B")

(list "D")

(list "E" "C" "F")

(list "F" "D" "G")

(list "G")))

Alternatively, we could have represented a graph as a list of edges:

; A Graph is [Listof (list String String)]

; Interp: a graph is a list of edges from one node to another

Under this definition, the graph above would be represented as:

(define G

(list (list "A" "B")

(list "A" "E")

(list "B" "E")

(list "B" "F")

(list "C" "D")

(list "C" "B")

(list "E" "C")

(list "E" "F")

(list "F" "D")

(list "F" "G")))

Re-develop the path function in light of this new representation:

; path : Graph String String -> [Maybe [Listof String]]

; Compute a path in the graph between the given nodes, if one exists

; Produces #false if no path exists

38.5 Types

Which of the following programs well-typed (according to Typed Racket’s type system)?

(: f : (All (A) (Number -> A) -> A))

(define (f x)

(x 3))

(: g : (U String Number) -> (U String Number))

(define (g x)

(cond [(string? x) (+ x 3)]

[(number? x) (string-append "hi" x)]))

(: h : (U String Number) -> (U String Number))

(define (h x)

(cond [(string? x) (string-append "hi" x)]

[(number? x) (+ x 3)]))

(: i : Number -> Real)

(define (i x)

(if (< x 10)

(sqr x)

(+ x 50)))

(: j : Number -> [Listof Number])

(define (j x)

(map (λ ([z : (Number -> Number)]) (z x))

(list add1 sqr sqrt)))

(: k : Number String -> [Listof String])

(define (k x y)

(cons (string-append (number->string x) y)))

Provide the most general valid type signature for the following functions. Provide type annotations needed for any λ parameters.

(define (lengths xs)

(map length xs))

(define (total-length xs)

(foldr (λ (x t) (+ (length x) t)) 0 xs))

(define (map-f-zero lof)

(map (λ (f) (f 0)) lof))

Challenge problem (nothing this tricky will be on the exam): provide the most general type signature and annotions for this function:

; Abstraction of outer "product" computations

(define (outer f l1 l2)

(cond [(empty? l2) '()]

[else (map (λ (m) (map (λ (n) (f m n)) l2)) l1)]))

39 November 30, 2018

Audio and video capture from today’s class is available here.

40 December 3, 2018

Audio and video capture from today’s class is available here.

41 December 5, 2018

Audio and video capture from today’s class is available here.