

The goal of this document is to provide students in CMSC411 (computer architecture) with a brief but thorough introduction to the "simple" model of computer memory presented in chapter 1 of Hennessey and Patterson's COMPUTER ARCHITECTURE: A QUANTITATIVE APPROACH, an understanding of which is necessary for later portions of the course (caching, etc.)
This document is presented in the style of a short hypertext FAQ list. FAQ is an acronym for the words, "Frequently Asked Questions." FAQs are widely used in online discussion groups (newsgroups, web-hosted discussions and so on), as technical support documents ("common questions") and so on. A wealth of information is available online in the form of FAQs, particularly for computing topics. Many of the FAQ sections are accompanied by exercises to illustrate the point. Students in computer science should be familiar with FAQs as sources of online information.
Answers to specific questions are available simply by jumping directly to the desired question, but the list is ordered by topic and the questions can be read sequentially as a quick tutorial. This document is not a substitute for the textbook material.
1. What is the "simple" model of computer memory? How do I visualize the computer's memory?
2. How is memory accessed? Why do we break memory into elements like "bytes" and "words"?
3. Are all words the same? (A few words about words)
4. Why did endian-ness arise? Are there any advantages to one over the other?
5. If it's all internal, why do I care?
6. What do I need to know about alignment?
7. What about some stats on current architectures?

For the purposes of this document, computer memory will be viewed by what we will call the "simple" model. It is important to realize that this is an idealized model that is substantially less layered than the model that is introduced toward the end of the course (caches, virtual memory, etc.). While the layers of complexity will change and details will be added to this model, it is typically the "simple" model that programmers will encounter and need to deal with directly. It is very important to keep in mind that this all models are an abstraction from the physical reality of computer memories and that this is a good thing. It is abstraction that allows computers to do useful work.
In the "simple" model, computer memory is a mono-dimensional ordered length of bits. This can be visualized as a series of bits, one after another in a line stretching out to infinity. Bits may not change their position in the line. They are numbered sequentially starting with zero.

This infinite length of ordered bits is called a Turing memory. Its size, the length of the line of bits, is infinite. In a binary machine, each bit may be set to either one or zero.
Here we encounter another abstraction. Note that this convention itself is merely a convenient abstraction and is purely arbitrary and used by convention for historical reasons. It would be just as valid to have named the states "on" and "off," "up" and "down," or "a" and "b," or "empty" and "full" or even "Zira" and "Cornelius."

The actual representation of bits in modern computers involves electrical levels, but had things gone differently we might have had mechanical computers based on spokes and ratchets if Babbage's machine had been finished, or bits stored as containers of liquid had computers evolved from water clocks instead of electrical contacts on a punch card reader. That reader was itself evolved from an automated loom - "linen" and "silk," anyone?
Of course, we can't have an infinite memory in any real world computer, whether we use electrical currents or spring-loaded dials, so now envision that the line is of a specific length, but all of the other properties -- a length of N ordered bits beginning at 0 and ending with bit number (N - 1). What can we do with such a memory?
The answer is "nothing" because we have not defined a way to access any element in the memory.
In computers, the location in memory of an element is called the element's address. Addressing is actually rather complicated in the real world because an address may map from an idealized or virtual address into one or more levels of physical addresses, one for each level in a computer's memory system. But in our idealized model, we will treat all addresses as absolute and unique. For our memory, no two elements will share the same address. The addresses should be thought of as a physical location on the "infinite line" or "line segment" that we are using to represent memory so it should be obvious that no two elements (bits, above) can share the same address, and no address can be "empty."
The simplest approach to accessing memory would be to access each bit by its position. Then we could access the first bit by going to address 0, the second by address 1, the third by address 2, the fourth by address 3 and so on.
Since we are using digital computers, all of the numbers we work with are eventually going to be stored in binary. In binary, we can represent 0 through 3 with just two bits:
00 0
01 1
10 2
11 3
So we need 2 bits to address 4 memory locations. Extending this, we can address 128 locations with 7 bits, and 1024 locations with a mere 10 bits. This seems relatively efficient. In practice, we don't want to store 128 bits or 1024 bits. We don't even want to store 1024 bytes, or even 1024 kilobytes. Most general purpose CPUs designed since 1986 can address 2^32 bytes (slightly more than 4 billion bytes) worth of memory, and CPUs designed as of around 1991 can address 2^64 bytes (4 billion bytes squared), though it would take years for any of one of them to actually scan through such a huge number of bits, even if anyone could build a memory system that large today.
Note that these measures are in bytes. 2^64 bytes worth of bits needs to deal with 8 bits per byte, or 2^3 bits per byte, but that comes to only only 67 bits, just 3 more bits overall.
Computer memories are not addressed at the bit level, however. One easy to understand reason for this is that a bit is just not a very meaningful unit to work with - to perform any kind of math using only bits would be quite difficult. To add two numbers together, you would have to add each bit in sequence, just as if you were building the equivalent of a ripple adder (CMSC311) from software. And how would you do multiplication, or comparisons between numbers? Such a machine would, in practice, be useless.
We want computers that are useful, so we need to divide memory up into useful units. These units will, in fact, define the capabilities of the computers we build. If we break memory into, say, 4 bit clumps of bits ("nibbles") we can store any value between 0 and 15 (think of converting binary to hexadecimal!) in a single nibble. This means that the adders and other circuits in our CPU also need to be able to work with 4 bit clumps, so now we can add 15 and 15 in a single operation instead of a bit at a time.
Oops. But if we add 15 and 15, we will end up with an answer of one. Why? Because our unit f storage can only store 0 through 15. When we add 15 and 15 together, we overflow the adder and the result is truncated. Obviously we can handle this by adding larger numbers a nibble at a time just as we could manually handle a bit at a time. But a nibble doesn't seem like a useful size. You can't even use a nibble to store the roman alphabet.
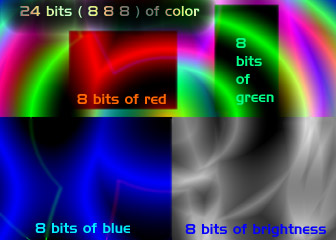
A byte is probably the first "clump" size that's actually useful. With a byte we can address the entire alphabet and all of the punctuation marks and symbols that we want to use in documents. 0 to 255 is also a fairly useful range for numbers on the small scale. Even if we're thinking about more entertaining uses for computers (a video game, for instance) the human eye can only see about 256 levels of grey (greyscale - ranging from black to white) so we can already use bytes to do very high quality images. If we want color we can use 3 bytes together, as red, green, and blue, and represent almost all of the colors that the eye can see (in fact, with 3 bytes, or twenty four bit color the display technology is the limiting factor). Bytes are pretty useful.
But they still aren't useful for real integer computation, where we want to deal with values with much wider ranges. And there's another limitation: if our largest unit is a byte, then the largest address we can access is that which a byte can represent. Suppose that we have a memory that is addressed on the byte level. With a single byte we can represent 256 locations, giving us a total memory size of only 256 bytes.
The next logical cluster size is twice the size of bytes, or 16 bits. With 16 bits addresses and 16 bit elements, which hereafter will be called "words," we can start to address a useful amount of memory. Specifically, a 16 bits gives us 65536 unique addresses, each of which can store 16 bits. This gives us 131072 bytes of total addressable memory, or 128 kilobytes. Now we're really talking, talking about 1968 or so.
Let's skip up to modern machines. Modern machines address between 4 gigabytes (32 bit machines) to 64 terabytes (64 bit machines). Obviously few machines have physical memory sizes in the 4 gig range (though they do exist) and none come even close to approaching having 2^64 bytes of memory. So why do we want such large address spaces?
Well, for two reasons.
One, as we can see above, we want to use large integers. A machine is typically defined as 64 or 32 bit by the width of its ALU registers, not by the number of memory elements it can represent. As an example, the Motorola 68000 (used in the original Apple Lisa, a failed precursor to the Macintosh as well as in the Macintosh itself, and in 1980s arcade games like Altered Beast and Gauntlet) was a 32 bit microprocessor that could only address 2^24 bytes, but it is still considered a 32bit CPU. However, the address space is always limited by the integer size, since that's used to store addesses, and the size of the element cannot be greater than that size, either (or else what would you do with what sits at the address?). So you could have a machine with 64 bit addresses that worked with nibbles or bytes, or 16 bit words and so on, but then you'd have to read multiple elements before you could do anything with them.
Two, it's very convenient to have a large address space to use for things besides memory, such as "memory mapped files" where files on the disk appear to the CPU and to programs as arrays in memory, or as space to allocate to hardware devices so that interacting with a device is similar to storing and reading values, or for things like the computer's ROM.
Or just for room to grow, which is very, very important. The original IBM PC design used the Intel 8088, which was a 16 bit CPU that could only address 1 megabyte of memory. The engineers designing the PC put the video display (the MDA, monochrome display adapter) , ROM and other devices in the address space from 640k to 1MB, meaning that programs saw a linear length of memory from the first 16bit word in memory to the last at the 640k threshold, and then everything else was used for devices and ROM and so on. The programs were all written to assume contiguous memory, and as a result real mode programs (including MSDOS and all the programs which run on it except those that use "extenders" [including EMS, XMS etc.]) are limited to 640k. Other 8088-based machines (the Dec Rainbow, the Zenith Z-100, etc.) also ran versions of MS-DOS (prior to 1983 there were several systems which ran MS-DOS and CP/M that were not "PC clones"), but because their designers made different choices, they could address more memory (960k, 768k). As anyone who uses PCs regularly can attest, the lack of "room to grow" imposed by this design is still with us in the form of innumerable workarounds and extenders.
Either way, memory is broken up into these larger units (words), and because most computers share common philosophical ancestors, those words are in turn broken up into bytes. Some machines can directly work with bytes within a word (Intel, PowerPC, and so on) and others need to get at the bytes within their words using shifting (Dec Alphas prior to the AXP 21164a could only access their 64bit words as such).
Here's a bit of trivia to round out this section: the computer described above, which can only work with individual bits, happens to be a Turing machine, and so, in theory, it could be made to do any of the operations described as difficult.
No, and welcome to Lilliput.
In the discussion above we have said nothing about the value of specific bits or bytes, but rather, discussed only issue such as the maximum value that can be represented and the number of combinations available in with a certain number of bits. This was quite deliberate, because the question of what kind of value the ordering imposes is not a settled matter, and may never be a settled matter.
The vocabulary associated with computing is nothing is not apt, what with words like "benchmark." Now we're going to introduce a new word and concept: endian-ness.
In his satirization of the political split between Protestantism and Catholocism, Swift's "Gulliver's Travels" introduces the citizens of Blefuscu and Lilliput, two islands locked in civil war over an important philosophical difference. The issue? When cracking open an egg, which side (the little, pointy end or the broad, wide "bottom" end) should be broken first.
The word "endian" comes from Gulliver's Travels, and the issue is very similar. Instead of concerning the question of which end of an egg to break, endian-ness in computers revolves around the issue of which order "chunks" should appear within memory.
This isn't a debate of where addressable elements (words) should be placed, since all of the elements are on equal footing. Rather, it concerns how data is ordered within those words, or more specifically, the order and importance of bytes within words.
Let's talk about importance and use numbers as an example. Take the number "123456." We group the digits in this number into sets of three, or "123,456." Which of these is the most important digit?
The answer is "1."
If you're thinking, "How can any of them be more important?" think of it this way. Suppose that in a fit of stupidity, you made a series of bad bets at the track, and you end up $123,456 in the hole. Now along comes your local area knee-capper, here to collect the vig. Now, if your local crime family wasn't sharp about choosing accountants, and if they made a mistake with an eraser and "forgot" any of those digits by converting it to a zero, which one would make you happiest? Obviously the 1 at the beginning has the most "weight."
We call this digit the "most significant digit." When we're dealing with computers, we have only bits, and so this digit is the "most significant bit" or "MSB." Conversely, if the accountants zeroed out the 6 at the end, they're only saving you $6, really an insignificant sum compared to the other $123,450. We call this digit the "least significant digit" and in computers the "least significant bit" or "LSB."
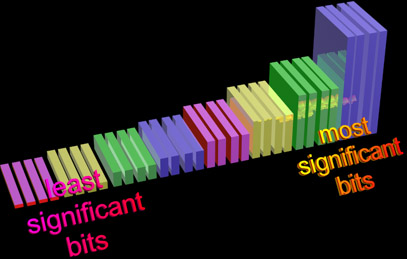
Now we can also extend this to our chosen "chunk." In our own base 10 system, we use chunks of three digits. In computers, we typically use bytes. The most significant "byte" is that which represents the bulk of the value in the word containing the byte. By convention, we write numbers (base 10, binary and otherwise) from left to right, starting with the most significant digit on the left.
Take this 16 bit word broken into its two constituent bytes:
| 0000 0001 | 1111 1111 |
Note that even though the first byte is almost all zeros, the single one, in the least significant bit within that byte is still the bit with the most weight in the word. Even though all of the other bits in the word are on, their total value is still 1 less than ½ the value of the word above.
That's how we write the number on paper. This left-to-right ordering with unique digits in specific positions within the number comes to us from Arabic. Other systems have existed historically, but almost everyone in the world writes numbers left to right (Chinese offers vertical, but it's similar in that the most significant digit comes first, and so on).
No such consensus exists for computers. Worse, there's no way to tell, if all you have is some binary data, how the bytes within a word were ordered. Let's take a look at that word again as it might be represented in the memory of two different computers (we're going to consider that the lowest address is to the left):
| most significant byte first: | 0000 0001 | 1111 1111 | |||
| least significant byte first: | 1111 1111 | 0000 0001 |
That's just two. With more than two bytes in our word, we could have some really interesting orderings. We could put the two middle bytes on the outside, or in some other arrangement. Fortunately, you don't find computers that do this much, though you should not be surprised to discover that these kinds of machines have existed at one point or another.
Now, from our point of view, shaped by our Arabic-derived number system, the first seems perfectly logical, so why should there be any disagreement? Well, let's visualize what these two orders look like in memory.
First of all, the value of bits within bytes is fairly standardized. Bit "0" is the "low order" bit, or the "least significant bit." If we envision memory as an array stretching off to the right, like:
bit address 0 -> 10101011 <- bit address 7
the first bit is the one on the left, it is bit 0, and it is the least significant bit in the array (which is a byte). Note that this is exactly the opposite of the common orthography we use when writing binary digits. Were we to write that byte of binary memory, we would write it from left to right with the most significant bit on the right, as:
bit address 7 -> 11010101 <- bit address 0
Remember, all of the words in memory are just locations, one after another, in a linear array of addresses, so by "first" we mean the first byte you encounter in words as you move from the "zero" end of that memory to the other end. It helps to visualize yourself as travelling along this line, as if it was a sort of line chart (like those used to display the stock market), with the height of a bit being it's value to the word as a whole).

Let's revisit our example above with the most significant byte first.
| most significant byte first: | 0000 0001 | 1111 1111 |
Now, if we were to write out the bits of memory holding this word, starting at the left with the first bit, we'd write:
bit address 0 -> 1000 0000 1111 1111 <- bit address 15
In other words, the least significant bit in a byte comes before the most significant bit. This is confusing because in our normal writing system, the infinite expanse stretches off to the LEFT. But we normally express arrays and lengths of raw memory from left to right (with the "end" of the array on the right).
Now let's visualize the memory in the big endian machine we're discussing as a roller coaster. For the sake of the discussion, we're going to assume that all of the bits are set to one instead of the string of zeroes as above.

At the start of the ride, we're at the least significant bit of the most significant byte in the (16 bit) word. The coaster starts to move. As we move forward in memory, we start to climb toward the most significant bit in the most significant byte in the word - this is as high as we're going to get.
The next bit after the most significant bit in the most significant byte is the least significant bit in the least significant byte in the word. You can't go lower, so as we come over the peak represented by the MSBit in the MSByte, we head STRAIGHT DOWN. And then, as we move forward in memory, we start to climb again, because we're moving from the LSBit in the LSByte to the MSBit in the LSByte. And then we're through the first word, and the rid starts over (there's just a small climb between the end of the word, the MSBit or the LSByte, and the LSBit of the MSByte - what are their relative values?).
So a big endian memory is a lot of ups and downs. Viewed as a line chart, where we plot the bit in memory against it's weight within its word, big endian memory looks like a series of ups and downs within each word.
The 32bit and 64bit analogs of the 16 bit words are just extrapolations - the most significant chunk comes first, the least significant chunk comes second. It takes a few tries to visualize a big endian memory clearly.
Since we've covered big endian, let's think about what little endian looks like. Here's our little endian (least significant byte first) word from above:
| least significant byte first: | 1111 1111 | 0000 0001 |
What does this look like in memory? Well, as with big endian, the least significant bit comes first in each byte. The difference here is that now the least significant byte comes first. So the first bit we see is the first bit in the least significant byte in the word and the last bit we see is the most significant bit in the most significant byte in the word.
bit address 0 -> 1111 1111 1000 0000 <- bit address 15
Let's go back to the roller coaster analogy and again assume that all of the bits in the word are set to one. At the beginning we start out with the LSBit of the LSByte in the word - as lot as you can go, in other words. Now the roller coaster starts to roll forward and we move forward in memory, climbing from the LSBit in the LSByte to the MSBit in the LSByte. Here's where things are different. The bit following the MSBit in the LSByte is the first bit of the next byte, or the LSBit in the MSByte. And so we keep climbing, up to the MSBit in the MSByte. And then our word is over, and we plummet STRAIGHT DOWN to the LSBit in the LSByte of the next word in memory.
In other words, the little endian roller coaster is very regular. Viewed as a line graph little endian memory looks like a simple saw tooth.
(A much, much broader discussion of the issues surrounding big and little endian can be found at http://www.isi.edu/in-notes/ien/ien-137.txt.3 )
Little endian looks a little simpler, because it's completely regular. You're probably thinking that with a pair of shift registers you could build a simple communications system between two little endian memories, because you could just transfer the bytes (no matter how many bytes are in a word) a bit at a time from one to another. This is true, but it doesn't really mean anything to modern CPUs, because they try to move at least a word at a time to and from memory and usually more than that.
On the other hand, big endian agrees with the way we write numbers on paper, by convention. If we ever have to look at memory directly, big endian makes a lot of sense. Another fact that shouldn't surprise you is that this is exactly what a lot of people had to do in the 60s and 70s, and so big endian architectures had an appeal in that hexadecimal dumps of their memory were easier to read.
This is the main question and the answer is that you may not care. But if you exchange data between computers, and this means over a serial line with modems (streams of bits ordered into bytes), or in the form of binary data files (basically just dumps of memory), or over a network (streams of bytes) , you need to understand endian-ness, because otherwise you wont recognize it or know how to deal with it.
You're not even safe on just one architecture if you write device drivers, because some of the devices you're trying to support may have an endian-ness that's the opposite of the main CPU. For years SCSI controller cards based on the Motorola 68010 shipped for Intel-based 80x86 systems, with a big endian CPU acting as the control hardware on the SCSI card trying to exchange data with the little endian CPU that ran the machine.
Now, if like most of the students in the class, you've used dialup modem connections, and used text between many different computers and never had any problem, you're probably thinking that the endian issue is overstated. Wouldn't you have run into it by now?
Probably not. Users almost never do, because it's been handled for them.
Text, for instance, is a stream of bytes. The order of bytes within words is completely unimportant because the unit of exchange is the byte, and that's how they're stored and used in memory.
Binary image files, like zip files, or bitmap formats like .jpg or .tiff, also appear to be unaffected, but this is because the endian-ness of the formats is well defined and systems that need to know to convert the byte ordering to their native representation as they read the data.
As a programmer, though, one needs to deal with endian-ness issues for users. This is where things get tricky and non-portable.
The easiest way to handle it is to use any language-defined method of hiding endian-ness. In fact, ASCII text is one of the easiest and most intuitive ways for programmers to deal with endian-ness, because they can use their programming language's standard input/output library to read/write numbers from/to text files, and leave it up to the standard library routines to convert the ASCII representation (in our normal left-to-right orthographic convention) into whatever internal format the CPU uses. This is as easy as it gets, because it hides endian-ness completely, but for large chunks of binary data, it's extremely inefficient, because each byte in the output file only stores 1 base 10 digit.
Other methods tag the file with a header that says what endian-ness the contained data is (for instance, Unicode [a 16 bit character set] has a 16bit stamp at the beginning of the file that allows the reading program to determine whether the data contained by the file was stored as big or little endian and switch as necessary).
If language portability is less of an issue than operating system portability, use the system to its full potential. NeXTSTEP/OpenStep offer typed streams to handle endian-ness issues, Windows NT defines a little endian platform to eliminate concerns of binary data portability, and other multiplatform operating systems have their own way of dealing with the problem, if they deal with it at all.