Combinatorics and Algorithms for Real Problems

Summer, 2016

Fun With Probability
Mentor: William Gasarch

If you roll two 6-sided dice then (1) the prob of getting a 2 is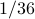 , but (2) the prob of getting a 7 is 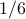. Hence sums are UNFAIR! Can you LOAD dice so that sums are fair. It is well known that, alas, you cannot. But how close can you come? What about other sets of dice?

Deep Learning
Mentor: Tom Goldstein

Neural networks are usually trained on one single worker (node) using simple back-propagation algorithms. When more computing power is needed to solve large problems, a GPU is often used to increase the computing power on that node. My group focused on implementing a range of training algorithm for neural networks using distributed computing tools that spread the work across many nodes in a large cluster. Both simple backpropagation algorithms, and also a variety of new Monte-Carlo algorithms, were implemented using the Message Passing Interface (MPI) to control many processes on a large computing system. Implementations were deployed on the Google Compute Engine to test performance in the cloud. Implementations were benchmarked against standard tools running on a GPU.

The Can't Stop Game
Mentor: Clyde Kruskal

The game Can't Stop depends on a combination of luck and skill. In this game a player rolls dice to get ahead, but can stop. If he doesn't stop in time he may lose all that he has gained that turn. For more on the game, including the rules, see here.
Monte Carlo techniques or game playing are ideal to study this game. We will learn these techniques and write programs to play the game well. We will then try to learn what the programming is really doing to make conjectures and prove theorems.
For a talk on research Clyde Kruskal (and co-authors) have already done on the 1-player version see here.

Data Center Scheduling
Mentor: Samir Khuller
In modern datacenters, technologies like MapReduce divide large problems into small jobs, which need to be scheduled on complex architectures. This project introduced a general framework that converts algorithms for offline scheduling and knapsack-type problems (in which the entire input is known upfront) to the online setting (i.e., the entire problem input is not available upfront). This framework is then used to produce algorithms that have the best known approximation performance for a variety of scheduling problems. The algorithms perform well on real world data sets.

Public Key Crypto Using Group Theory
Mentor: Jonathan Katz
In Public Key Crypto Alice and Bob can set up a system where they can communicate secretly without ever having to meet! This is usually done using Number Theory. Recently there have been some schemes that use Group Theory. Are they secure? Lets look at them and find out!