10 Arrays

8.17

contents ← prev up next →

10 Arrays🔗

10.1 Array vs Sequence

10.6 Dutch national flag

10.7 Selection Sort

10.8 Optional Reading: Monotonicity Lemma

10.9 Optional Reading: Insertion Sort

10.9.1 Shuffling

10.9.2 Shifting

10.10 Optional Reading: Coincidence Count

In this lecture, we’ll examine programs that use loops to work with arrays. Specifically, we’ll focus on search algorithms that either find particular elements or identify properties within an array. A key part of our discussion will be understanding how to derive loop invariants from the postconditions that these programs are meant to achieve.

Arrays are similar to the sequences we’ve encountered earlier, but with one important distinction: arrays are mutable, meaning their elements can be changed. Before we delve into algorithms that operate on arrays, let’s first revisit the differences between arrays and sequences.

10.1 Array vs Sequence🔗

The (fixed) size of an array a is given by a.Length, whereas the (fixed) size of a sequence s is given by |s|.
The elements of arrays and sequences are accessed in the same way.
```
y := a[i];
y := s[i];
```
A sequence is entirely characterized by its length and its elements.
```
  if |s| == |t| && forall k :: 0 <= k < |s| ==> s[k] == t[k] {
    assert s == t;
  }
```
But that’s not true for arrays. Each array has an identity. In other words, an array is a reference to a sequence of elements. The follwoing assertion is true for sequences, but not necessarily for arrays.
```
if a.Length == b.Length && forall k :: 0 <= k < a.Length ==> a[k] == b[k] {
assert a == b; 
}
```
One can construct a sequence from a range of array elements. The general form is a[i..j], which says to take the first j elements of the array and then drop the first i elements. If i is omitted, if defaults to 0, and if j is omitted, it defaults to a.Length. Omitting both, the expression a[..] is the sequence of all elements of the array.
```
  var u: seq<X>;
  u := a[i..j];
  u := a[0..j];
  assert u == a[..j];
  u := a[i..a.Length];
  assert u == a[i..];
  u := a[0..a.Length];
  assert u == a[..];
```
To create a new array, you must use a new assignment. Since this is a statement, it can only appear within method bodies—not function bodies. The elements of the new array are initialized using a specified function that maps indices to values, similar to how sequences are constructed. This initialization can be omitted if the array size is zero or if the element type is an auto-init type—one for which the compiler can automatically generate default values. Primitive types like int, real, bool, char, and bitvectors are generally auto-init types.
```
  u := seq(100, i => x);
  var c: array<X> := new X[100](i => x);
  var a: array<int> := new int[100]; 
```

Unlike sequences, arrays can be multidimensional. Here is an example of a 2-dimensional array, or a matrix.


  var m: array2<real> := new real[20, 30];
  var z := m[12, 22];
  assert m.Length0 == 20 && m.Length1 == 30;

10.2 Binary Search🔗

Our first algorithm is a classic in computer science: binary search. It derives its name from the way it repeatedly halves the search space with each iteration. As a result, its running time is logarithmic relative to the length of the array. For binary search to work correctly, the input array must be sorted in advance.

The diagram below provides a visual representation of the binary search invariant.

The termination of the loop is established using the metric hi - lo, which Dafny automatically uses as the default decreases clause in this case. This means we don’t need to write decreases hi - lo explicitly. Dafny determines a default decreases clause by inspecting the loop guard. If the guard is a comparison such as lo < hi or lo != hi, the default metric is the absolute difference between the two expressions being compared.

Dafny

datatype Option<X> = None | Some(value: X)

method BinarySearch(a: array<int>, key: int)
                                       returns (r: Option<int>)
  requires forall i, j :: 0 <= i < j < a.Length ==> a[i] <= a[j]
  ensures r.Some? ==> 0 <= r.value < a.Length && a[r.value] == key
  ensures r == None ==> key !in a[..]
{
  var lo, hi := 0, a.Length;
  while lo < hi
    invariant 0 <= lo <= hi <= a.Length
    invariant key !in a[..lo] && key !in a[hi..]

  {
    var m := lo + (hi - lo) / 2;
    if key < a[m] {
      hi := m;
    } else if a[m] < key {
      lo := m + 1;
    } else {
      return Some(m);
    }
  }
  return None;
}

10.3 Find Minimum🔗

Our next program is a straightforward linear scan to find the minimum value of an array. We’ll gradually build up the specification and program. We will use a loop index a, which starts from 0 and goes up to a.Length.

We form the loop invariant by replacing the constant ‘a.Length‘ in the postcondition with the variable ‘n‘. This loop invariant speaks of "what we’ve computed so far", which is one of many common forms of loop invariants.

From the assignment ‘n := n + 1‘, we can "compute backwards" (as we’ve seen in the previous lectures) to get a strong hint of how to fill in the loop body.

Dafny

method FindMin(a: array<int>) returns (m: int)
  requires a.Length != 0
  ensures forall i :: 0 <= i < a.Length ==> m <= a[i]
  ensures m in a[..]
{
  m := a[0];
  var n := 1;
  while n < a.Length
    invariant 1 <= n <= a.Length
    invariant forall i :: 0 <= i < n ==> m <= a[i]
    invariant m in a[..]
  {
    if a[n] < m {
      m := a[n];
    }
    n := n + 1;
  }
}
method TestFindMin(){
  var a := new int[5];
  a[0], a[1], a[2], a[3], a[4] := 9, 4, 6, 3, 8 ;
  //assert a[0] == 9 && a[1] == 4 && a[2] == 6 && a[3] == 3 && a[4] == 8;
  var m := FindMin(a);
  assert m == 3;
}

10.4 Find Zero🔗

Dafny

method FindZero'(a: array<int>) returns (index: int)
  ensures index < 0 ==> forall i :: 0 <= i < a.Length ==> a[i] != 0
  ensures 0 <= index ==> index < a.Length && a[index] == 0
{
  index := 0;
  while index < a.Length
    invariant 0 <= index <= a.Length
    invariant forall k :: 0 <= k < index ==> a[k] != 0
  {
    if a[index] == 0 {
      return;
    }
    index := index + 1;
  }
  index := -1;
}

method TestFind0() {
  var a: array<int> := new int[5][9, 14, 6, 0, 8];
  assert a[0] == 9 && a[1] == 14 && a[2] == 6 && a[3] == 0 && a[4] == 8;
  var r :=FindZero(a);
  assert forall i :: 0 <= i < 3 ==> a[i] != 0;
  assert r == 3;
}

10.5 Updating Arrays🔗

Methods must declare all arrays they are allowed to modify. A caller of a method may assume that every other array retains its valye.

Dafny

method SetEndPoints(a: array<int>, left: int, right: int)
  requires a.Length != 0
  modifies a
  ensures a.Length > 1 ==> a[0] == left
  ensures a[a.Length-1]==right
{
  a[0] := left;
  assert a[0] == left;
  a[a.Length - 1] := right;
  assert a[a.Length-1]==right;
}
method TestSetEndPoints() {
  var a: array<int> := new int[5][9, 14, 6, 0, 8];
  assert a[0] == 9 && a[1] == 14 && a[2] == 6 && a[3] == 0 && a[4] == 8;
  SetEndPoints(a,0,100);
  assert a[0] == 0;
  assert a[4] == 100;
}

Array variables are allowed to alias each other, or have identical values.

Dafny

method Aliases(a: array<int>, b: array<int>)
  requires 100 <= a.Length
  modifies a
{
  a[0] := 100;
  var c := a;
  if b == a {
    b[10] := b[0] + 1;
  }
  c[20] := a[14] + 2;
}

The old syntax lets us refer, in postconditions, to the values of arrays when the function was called.

Dafny

method UpdateElements(a: array<int>)
  requires a.Length == 10
  modifies a
  ensures old(a[4]) < a[4]
  ensures a[6] <= old(a[6])
  ensures a[8] == old(a[8])
{
  a[4], a[8] := a[4] + 3, a[8] + 1;
  a[7], a[8] := 516, a[8] - 1;
}

Note that old has an effect on array dereferencing but not on values of function parameters.

Dafny

method OldVsParameters(a: array<int>, i: int) returns (y: int)
  requires 0 <= i < a.Length
  modifies a
  ensures old(a[i] + y) == 25
  //ensures old(a[i]) + y == 25

A confusion about that behavior leads to the following bad specification. How should we modify the ’ensures’ clause?

Dafny

method Increment(a: array<int>, i: int)
  requires 0 <= i < a.Length
  modifies a
  ensures a[i] == old(a)[i] + 1
  // ensures a[i] == old(a[i]) + 1
{
  a[i] := a[i] + 1;
}

A method may return a new array.

Dafny

method NewArray() returns (a: array<int>)
  ensures a.Length == 20
{
  a := new int[20];
  var b := new int[30];
  a[6] := 216;
  b[7] := 343;
}

However, we must declare that the return value is fresh if we want a caller to know this array is safe to modify, as it doesn’t alias others from the call.

Dafny

method NewArray'() returns (a: array<int>)
  ensures a.Length == 20
  ensures fresh(a)
{
  a := new int[20];
  var b := new int[30];
  a[6] := 216;
  b[7] := 343;
}

method Caller() {
  var a := NewArray'();
  a[8] := 512;
}

Functions may read but not write arrays, and they must declare which arrays they read.

Dafny

predicate IsZeroArray(a: array<int>, lo: int, hi: int)
  requires 0 <= lo <= hi <= a.Length
  reads a
  decreases hi - lo
{
  lo == hi || (a[lo] == 0 && IsZeroArray(a, lo + 1, hi))
}

No such clause is required for the analogous function on sequences.

Dafny

predicate IsZeroSeq(a: seq<int>, lo: int, hi: int)
  requires 0 <= lo <= hi <= |a|
  decreases hi - lo
{
  lo == hi || (a[lo] == 0 && IsZeroSeq(a, lo + 1, hi))
}

Let’s now practice initializing arrays using loops.

Dafny

method InitArray<T>(a: array<T>, d: T)
  modifies a
  ensures forall i :: 0 <= i < a.Length ==> a[i] == d
{
  var n := 0;
  while n != a.Length
    invariant 0 <= n <= a.Length
    invariant forall i :: 0 <= i < n ==> a[i] == d
  {
    a[n] := d;
    n := n + 1;
  }
}

The same is doable in two dimensions.

Dafny

method InitMatrix<T>(a: array2<T>, d: T)
  modifies a
  ensures forall i, j :: 0 <= i < a.Length0 && 0 <= j < a.Length1
           ==> a[i, j] == d
{
  var m := 0;
  while m != a.Length0
    invariant 0 <= m <= a.Length0
    invariant forall i, j :: 0 <= i < m && 0 <= j < a.Length1
              ==> a[i, j] == d
  {
    var n := 0;
    while n != a.Length1
      invariant 0 <= n <= a.Length1
      invariant forall i, j :: 0 <= i < m && 0 <= j < a.Length1
                ==> a[i, j] == d
      invariant forall j :: 0 <= j < n ==> a[m, j] == d
    {
      a[m, n] := d;
      n := n + 1;
    }

    m := m + 1;
  }
}

We can also modify prior array values.

Dafny

method IncrementArray(a: array<int>)
  modifies a
  ensures forall i :: 0 <= i < a.Length ==> a[i] == old(a[i]) + 1
{
  var n := 0;
  while n != a.Length
    invariant 0 <= n <= a.Length
    invariant forall i :: 0 <= i < n ==> a[i] == old(a[i]) + 1
    invariant forall i :: n <= i < a.Length ==> a[i] == old(a[i])
  {
    // The sequence of 'assert' commands here documents how we realize the need
    // for the final loop invariant.
    assert a[n] + 1 == old(a[n]) + 1;
    a[n] := a[n] + 1;
    assert forall i :: 0 <= i < n ==> a[i] == old(a[i]) + 1;
    assert a[n] == old(a[n]) + 1;
    assert forall i :: 0 <= i < n + 1 ==> a[i] == old(a[i]) + 1;
    n := n + 1;
    assert forall i :: 0 <= i < n ==> a[i] == old(a[i]) + 1;
  }
}

Note that this copying routine works even if the two arrays alias.

Dafny

method CopyArray<T>(src: array<T>, dst: array<T>)
  requires src.Length == dst.Length
  modifies dst
  ensures forall i :: 0 <= i < src.Length ==> dst[i] == old(src[i])
  ensures dst[..] == old(src[..])
{
  var n := 0;
  while n != src.Length
    invariant 0 <= n <= src.Length
    invariant forall i :: 0 <= i < n ==> dst[i] == old(src[i])
    invariant forall i :: 0 <= i < src.Length ==> src[i] == old(src[i])
  {
    dst[n] := src[n];
    n := n + 1;
  }
}
// Or using the aggregates:
method CopyArray'<T>(src: array<T>, dst: array<T>)
  requires src.Length == dst.Length
  modifies dst
  ensures forall i :: 0 <= i < src.Length ==> dst[i] == old(src[i])
  ensures dst[..] == old(src[..])
{
  forall i| 0 <= i <src.Length{
    dst[i]:=src[i];
  }
}

Here are some examples of handy syntax for initializing an array by giving a function to produce its elements.

Dafny

method MakeSomeArrays(F: int -> int, n: nat, d: int)
{
  var a1 := new int[25](F);
  var a2 := new int[25](i => i * i);
  var a3 := new int[n](_ => 0);
  var a4 := new int[50, 50]((i, j) => if i == j then d else 0);
  var b := new int[a1.Length](i requires 0 <= i < a1.Length reads a1 => a1[i]);
  // Note how this last example needs precondition information on an anonymous
  // function, to make an array access legal.
}

A similar feature is available for sequences.

Dafny

method MakeASequence()
{
  var s : seq<bool> := seq(500, i => i % 2 == 0);
}

Check out the following examples of aggregate statements, to modify many array cells at once without loops.

Dafny

method Aggregate1(a: array<int>)
  ensures forall i :: 0 <= i < a.Length ==> a[i] == old(a[i]) + i * i
  modifies a
{
  forall i | 0 <= i < a.Length {
    a[i] := a[i] + i * i;
  }
}

method Aggregate2(a: array<int>)
  ensures forall i :: 0 <= i < a.Length ==> a[i] == if i % 2 == 0 then old(a[i]) + 1 else old(a[i])
  modifies a
{
  forall i | 0 <= i < a.Length && i % 2 == 0 {
    a[i] := a[i] + 1;
  }
}

method Aggregate3<T>(a: array2<T>, d: T)
  ensures forall i, j :: 0 <= i < a.Length0 && 0 <= j < a.Length1 ==> a[i, j] == d
  modifies a
{
  forall i, j | 0 <= i < a.Length0 && 0 <= j < a.Length1 {
    a[i, j] := d;
  }
}

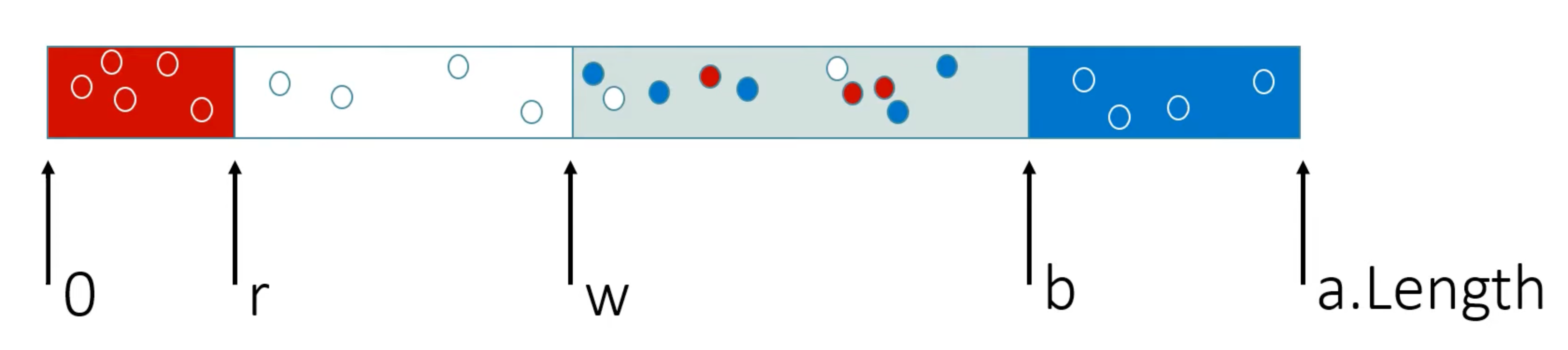
Dafny has heuristics to confirm it can enumerate all possible values of the variables used in an aggregate statement.

10.6 Dutch national flag🔗

Here’s an idiosyncratic sorting algorithm over arrays with elements from the following type, with the given "<=" predicate.

Dafny

datatype Color = Red | White | Blue

ghost predicate Below(c: Color, d: Color) {
  c == Red || c == d || d == Blue
}

method DutchFlag(a: array<Color>)
  modifies a
  // the final array is sorted.
  ensures forall i, j :: 0 <= i < j < a.Length ==> Below(a[i], a[j])

  // "after" state of the array is a permutation of "before"
  ensures multiset(a[..]) == old(multiset(a[..]))
{
  var r, w, b := 0, 0, a.Length;
  while w < b
    invariant 0 <= r <= w <= b <= a.Length
    // The array is divided into four regions
    invariant forall i :: 0 <= i < r ==> a[i] == Red
    // The first region is all red.
    invariant forall i :: r <= i < w ==> a[i] == White
    // The second region is all white.
    invariant forall i :: b <= i < a.Length ==> a[i] == Blue
    // The fourth region is all blue.
    // We don't know what's in there.
    // When the loop begins, all cells are in the third region.
    invariant multiset(a[..]) == old(multiset(a[..]))
  {
    // swap and adjustment region boundaries
    match a[w]
    case Red =>
      a[r], a[w] := a[w], a[r];
      r, w := r + 1, w + 1;
    case White =>
      w := w + 1;
    case Blue =>
      a[w], a[b-1] := a[b-1], a[w];
      b := b - 1;
  }
}

10.7 Selection Sort🔗

Now a slow sort that is able to work on infinite element types.

Dafny

method SelectionSort(a: array<int>)
  modifies a
  ensures forall i, j :: 0 <= i < j < a.Length ==> a[i] <= a[j]
  ensures multiset(a[..]) == old(multiset(a[..]))
{
  var n := 0;
  while n != a.Length
    invariant 0 <= n <= a.Length
    invariant forall i, j :: 0 <= i < j < n ==> a[i] <= a[j]

    // all elements already sorted are less than or equal to all
    // elements not sorted yet.
    invariant forall i, j :: 0 <= i < n <= j < a.Length
              ==> a[i] <= a[j]

    invariant multiset(a[..]) == old(multiset(a[..]))
  {
    var mindex, m := n, n + 1;
    while m != a.Length
      invariant n <= mindex < m <= a.Length
      invariant forall i :: n <= i < m ==> a[mindex] <= a[i]
    {
      if a[m] < a[mindex] {
        mindex := m;
      }
      m := m + 1;
    }
    a[n], a[mindex] := a[mindex], a[n];
    n := n + 1;
  }
}

Here is another version of the Selection Sort.

Dafny

predicate Ordered(a: array<int>, left: nat, right: nat)
  reads a
  requires left <= right <= a.Length
{
  forall i: nat :: 0 < left <= i < right ==> a[i-1] <= a[i]
}

method SelectionSort'(a: array<int>)
  modifies a
  ensures Ordered(a,0,a.Length)
  ensures multiset(a[..]) == old(multiset(a[..]))
{
  for i := 0 to a.Length
    invariant 0 <= i <= a.Length
    invariant Ordered(a,0,i)
    invariant multiset(a[..]) == old(multiset(a[..]))
  {
    var minValue := a[i];
    var  mindex := i;
    for j:= i + 1 to a.Length
      invariant mindex < a.Length
    {
      if a[j] < minValue {
        mindex := j;
      }
    }
    if i != mindex {
      a[i], a[mindex] := a[mindex], a[i];
    }
  }
}

10.8 Optional Reading: Monotonicity Lemma 🔗

Local-to-global monotonicity lemma

Dafny

lemma MonotoneBetween(c: seq<int>, i: int, j: int)
  // adjacent elements are sorted
  requires forall t :: 0 <= t < |c| - 1 ==> c[t] <= c[t+1]
  requires 0 <= i < j < |c|
  ensures c[i] <= c[j]
{
  if j == i + 1 {
    // base case: follows directly from the requires
  } else {
    // inductive step: prove for (i, j-1) and extend to (i, j)
    MonotoneBetween(c, i, j-1);
    assert c[i] <= c[j-1];
    assert c[j-1] <= c[j]; // from requires
    assert c[i] <= c[j];   // chain
  }
}

// The general statement
lemma monotonic(c: seq<int>)
  requires forall t :: 0 <= t < |c| - 1 ==> c[t] <= c[t+1]
  ensures forall i, j :: 0 <= i < j < |c| ==> c[i] <= c[j]
{
  forall i, j | 0 <= i < j < |c|
    ensures c[i] <= c[j]
  {
    MonotoneBetween(c, i, j);
  }
}

10.9 Optional Reading: Insertion Sort🔗

Dafny

predicate sorted(a: array<int>, l: int, u: int)
  reads a
  requires 0 <=l <=u <= a.Length
{
  forall i, j :: l <= i < j < u  ==> a[i] <= a[j]
}

In insertion sort, when the element to be inserted is smaller than the preceding element, there are two common ways to place it correctly:

Shuffling: The element being inserted is repeatedly swapped with its preceding element as long as that element is larger. This process continues until the new element reaches its proper position in the sorted portion. It requires multiple explicit swap operations.
Shifting: Each element in the sorted portion that is larger than the one being inserted is moved one position to the right, creating space for the new element. The new element is then placed in the correct position. This approach uses a temporary variable and avoids repeated swaps.

10.9.1 Shuffling🔗


[3, 10, 8, 2, 7] → 
[3, 8, 10, 2, 7] →
[3, 8, 2, 10, 7] → 
[3, 2, 8, 10, 7] →
[2, 3, 8, 10, 7] →
[2, 3, 8, 7, 10]

For this algorith, in each step of the shuffle the new array is the permutation of the old array. Therefore,

multiset(a[..]) == multiset(old(a[..]))

holds during the shuffle.

Dafny

method insertion_sort_shuffle(a: array<int>)
  modifies a
  requires a.Length >= 2
  ensures sorted(a, 0,a.Length)
  ensures multiset(a[..]) == multiset(old(a[..]))
{
  var i:= 1;
  while i < a.Length
    invariant 1 <= i <= a.Length
    invariant sorted(a, 0, i)
    invariant multiset(a[..]) == multiset(old(a[..]))
  {
    var j := i;
    while j >= 1 && a[j-1] > a[j]
      invariant 0 <= j <= i
      invariant forall k,l:: 0 <= k < l <= i && j != l ==>
                               a[k] <= a[l]
      invariant multiset(a[..]) == multiset(old(a[..]))
    {
      a[j-1], a[j] := a[j], a[j-1];
      j := j - 1;
    }
    i := i + 1;
  }
}

10.9.2 Shifting🔗


Let us insert item 2 into the correct position. 
[3, 8, 10, 2, 7] →
key = 2 //remember the current item
[3, 8, 10, 10, 7] → //move everything that is greater than key
[3, 8, 8, 10, 7] →
[3, 3, 8, 10, 7] →
now, swap key 2 with the current position
[2, 3, 8, 10, 7]

For this algorith, during the shuffle, the new array is NOT the permutation of the old array. Therefore,


multiset(a[..]) == multiset(old(a[..]))  // does not hold, but 
multiset(a[..][j:=key]) == multiset(old(a[..]))  // holds.

Dafny

method insertion_sort_swap(a: array<int>)
  modifies a
  ensures sorted(a,0,a.Length)
  requires 0 < a.Length
  ensures multiset(a[..])==multiset(old(a[..]) )
  //requires forall k::0 <=k < a.Length ==> 1< a[k]< 15
{
  var i := 1;
  while i < a.Length
    invariant 1 <= i <= a.Length
    invariant sorted(a,0,i)
    invariant multiset(a[..]) == multiset(old(a[..]))
  {
    var key := a[i];
    var j := i;
    while j > 0 && a[j-1] > key
      invariant sorted(a,0,i)
      invariant forall k :: j <= k <= i ==> key <= a[k]
      invariant i == j || sorted(a,0,i+1)
      invariant multiset(a[..][j:=key]) == multiset(old(a[..]))
    {
      a[j] := a[j-1];
      j := j - 1;
    }
    assert sorted(a,0,i+1);
    a[j] := key;
    i := i + 1;
  }
}

Now, we can test both versions of the Insertion Sort.

Dafny

method Main() {
  var a := new int[5][9, 14, 6, 3, 8];
  insertion_sort_swap(a);
  var k := 0;
  while(k < a.Length) { print a[k], ","; k := k+1;}
  print "\n";

  var b:=new int[][1,4,8,3,2];
  insertion_sort_shuffle(b);
  print (a[..]),"\n";

  var c:=new int[][1,2,3,4,5];
  var d:=multiset(c[..][2:=10]); // replace 3 with 10
  print (d),"\n";
}

10.10 Optional Reading: Coincidence Count🔗

Coincidence Count is the problem of computing how many elements are shared between two ordered arrays. Some variations of this problem assume that the arrays contain no duplicates. However, this implementation allows duplicate elements. For example, the Coincidence Count of the arrays [1, 1, 1, 2, 3, 3, 4] and [1, 1, 2, 2, 2, 4, 4] is 4, because they share four elements: two 1s, one 2, and one 4.

Here is the implementation from the, which uses multiset

Dafny

  lemma MultiSetInsertPrefix(a:array<int>, b:array<int>,
                            m:nat, n:nat)
  requires m <a.Length && n < b.Length
  requires a[m] == b[n]
  ensures multiset(a[m..]) * multiset(b[n..]) ==
          multiset{a[m]} + multiset(a[m+1..]) * multiset(b[n+1..])
{
  var E := multiset{a[m]};
  calc{
    multiset(a[m..]) * multiset(b[n..]);
    {assert a[m..] == [a[m]] + a[m+1..] &&
            b[n..] == [b[n]] + b[n+1..];}
    (E + multiset(a[m+1..])) * (E + multiset(b[n+1..]));
  }
}
lemma MultisetIntersectionAdvance(a:array<int>,
                                  m:nat, b:multiset<int>)
  requires m < a.Length && a[m] !in b
  ensures multiset(a[m..]) * b == multiset(a[m+1..]) * b
{
  var E := multiset{a[m]};
  calc{
    multiset(a[m..]) * b;
    {assert a[m..] == [a[m]] + a[m+1..];}
    (E + multiset(a[m+1..])) * b;
    (E * b) + multiset(a[m+1..]) * b;
    {assert E * b == multiset{};}
    multiset{} + multiset(a[m+1..]) * b;
    multiset(a[m+1..]) * b;
  }
}
method CoincidenceCount(a:array<int>, b:array<int>) returns (c:nat)
  requires forall i,j::0 <= i < j<a.Length ==> a[i]<=a[j]
  requires forall i,j::0 <= i < j<b.Length ==> b[i]<=b[j]
  ensures c == |multiset(a[..]) * multiset(b[..])|
{
  var i,j:=0,0;
  c := 0;
  while i < a.Length && j < b.Length
    invariant 0 <= i <= a.Length
    invariant 0 <= j <= b.Length
    invariant c + |multiset(a[i..]) * multiset(b[j..])| ==
              |multiset(a[..]) * multiset(b[..])|
  {
    var ai:= multiset(a[i..]);
    var bj := multiset(b[j..]);
    var ai2:=multiset(a[i+1..]);
    var bj2 := multiset(b[j+1..]);
    assert c + | ai * bj| == |multiset(a[..]) * multiset(b[..])|;
    if a[i] == b[j]{
      assert c + |ai * bj| == |multiset(a[..]) * multiset(b[..])|;
      assert c + |multiset({a[i]})| + |ai2 * bj2 |
          == |multiset(a[..]) * multiset(b[..])|
      by {MultiSetInsertPrefix(a,b,i,j);}
      c:=c+1;
      i:=i + 1;
      j := j + 1;
    }else if a[i] < b[j]{
      MultisetIntersectionAdvance(a,i,bj);
      i := i +1;
    }else if b[j] < a[i]{
      calc{
        ai * bj;
        bj *  ai;
        {MultisetIntersectionAdvance(b,j,ai);}
        bj2  * ai;
        ai * bj2;
      }
      j:= j+ 1;
    }
  }
}
method TestCoincidenceCount(){
  var a := new int[][1,1,1,2, 3,3,4];
  var b := new int[][1,1,2,2,2,4,4];
  var v:multiset<int> := multiset(a[..]) * multiset(b[..]);
  assert a[..] == [1,1,1,2,3,3,4];
  assert b[..] == [1,1,2,2,2,4,4];
  assert multiset(a[..]) * multiset(b[..]) == multiset([1,1,2,4]);
  var c:= CoincidenceCount(a,b);
  assert c == 4;
}

In the following implementation of Coincidence Count, we define a function that returns the set of elements common to two given sequences. The Coincidence Count is then given by the cardinality of this set, expressed as |InBoth(a[..], b[..])|.

We choose the "what’s left to be done" invariant. Here are three possible termination metrics:

```
decreases a.Length - m + b.Length - n
```
```
decreases a.Length - m, b.Length - n
```

decreases a.Length - m, if m < a.Length then b.Length - n else -1

Dafny chooses the third of these as the default ‘decreases‘ clause.

Dafny

function InBoth(s: seq<int>, t: seq<int>): set<int> {
  set x | x in s && x in t
}
method CoincidenceCount1(a: array<int>, b: array<int>)
                         returns (c: nat)
  requires forall i, j :: 0 <= i < j < a.Length ==> a[i] < a[j]
  requires forall i, j :: 0 <= i < j < b.Length ==> b[i] < b[j]
  ensures c == |InBoth(a[..], b[..])|
{
  var m, n := 0, 0;
  c := 0;
  while m < a.Length && n < b.Length
    invariant 0 <= m <= a.Length && 0 <= n <= b.Length
    invariant |InBoth(a[..], b[..])| == c + |InBoth(a[m..], b[n..])|
  {

    if a[m] == b[n] {
      assert InBoth(a[m..], b[n..]) ==
             {a[m]} + InBoth(a[m + 1..], b[n + 1..]);
      assert |InBoth(a[m..], b[n..])| ==
             1 + |InBoth(a[m + 1..], b[n + 1..])|;
      assert |InBoth(a[..], b[..])| ==
             c + 1 + |InBoth(a[m + 1..], b[n + 1..])|;

      c, m, n := c + 1, m + 1, n + 1;

      assert |InBoth(a[..], b[..])| == c + |InBoth(a[m..], b[n..])|;
    } else if a[m] < b[n] {
      assert InBoth(a[m..], b[n..]) == InBoth(a[m + 1..], b[n..]);
      m := m + 1;
    } else {
      assert InBoth(a[m..], b[n..]) == InBoth(a[m..], b[n + 1..]);
      n := n + 1;
    }
  }
}

contents ← prev up next →

	Syllabus
	Texts
	Schedule
	Notes
	Assignments
	Midterms
	Final
	Software

1	Dafny Cheatsheet
2	Dafny Basics
3	Getting Started with Dafny
4	Dafny Collections
5	Floyd Hoare Logic
6	Inductive Proofs
7	Inductive Types
8	Sorting
9	Loop Invariants
10	Arrays
11	SAT Solvers
12	Solving SAT and SMT Problems Using Z3

10.1	Array vs Sequence
10.2	Binary Search
10.3	Find Minimum
10.4	Find Zero
10.5	Updating Arrays
10.6	Dutch national flag
10.7	Selection Sort
10.8	Optional Reading: Monotonicity Lemma
10.9	Optional Reading: Insertion Sort
10.10	Optional Reading: Coincidence Count