12 Solving SAT and SMT Problems Using Z3

Before you start this section, make sure have a Python 3 installation available. You can check if this is the case by running python3, which should open a Python session.

You will also need to install the Z3 SMT solver and its Python bindings. Please follow the instruction at Insatll Z3 to install Z3 solver.

Now to check that everything was correctly installed, start a Python session and run:

from z3 import *

12.1 Review of Logical Operators🔗

First, we’ll do a quick review of some useful logical operators.

And(x, y) is true iff x and y are true.
Or(x, y) is true iff x or y are true.
Not(x) is true iff x is false.
Implies(x, y) (x ==> y) is true iff x is true implies that y is true.

It is common to write truth tables to describe the behavior of these operators.

We show the tables for And, Or, and Implies below.

And

Implies

a	b	a && b
true	true	true
true	false	false
false	true	false
false	false	false

a	b	a \|\| b
true	true	true
true	false	true
false	true	true
false	false	false

a	b	a ==> b
true	true	true
true	false	false
false	true	true
false	false	true

12.2 SAT & SMT🔗

Suppose we want to find a satisfying assignment for the expression (a || !b) && (!a || c). That means we’re looking for values of a, b, and c that make the entire expression evaluate to true.

One way to approach this is by checking all possible combinations of truth values for a, b, and c. Since each variable can be either true or false, there are 2^3=8 possible combinations.

Can you list all 8 combinations of a, b, and c?

In general, for n variables, there will be 2^n possible assignments, so the approach of "trying everything" is not efficient for large n. In fact, this is the SAT ("satisfiability") problem, which is NP-complete, meaning that it is "one of the hardest problems to which solutions can be verified quickly. But this difficult problem is exactly what tools like the Z3 SMT solver! Here’s how we can solve the problem using the Z3:


from z3 import *
a = Bool('a')
b = Bool('b')
c = Bool('c')

s = Solver()
s.add(Or(a, Not(b))) # a || !b
s.add(Or(Not(a), c)) # !a || c
s.check() # do these equations have a solution?
s.model() # get the solution

# Output: [b = False, a = False, c = False]

The output says that the formula (a || !b) && (!a || c) will be true when a, b, and c are all false.

But what if we want a different solution?

In this case, we can add an additional constraint that says that we don’t want the solution where a, b, and c are all false.


s.add(Not(And(Not(a), Not(b), Not(c))))
s.check()
s.model()

# Output: [b = False, c = True]

This output says that the formula (a || !b) && (!a || c) will be true when b is false and c is true (it doesn’t matter what a is).

Let’s try adding one more constraint:


s.add(And(Not(a), b))
s.check()

# Output: unsat

The output unsat means unsatisfiable. The solver is telling us that there is no possible choice of a, b, c that makes the current constraints true.

Z3 can find solutions to more than just SAT problems – it is an SMT solver.

SMT stands for SAT modulo theories; it generalizes SAT to formulas involving integers, strings, arrays, and so on. For example, we can use Z3 to find a solution for the system of equations 3x - 2y = 1, y - x = 1.


from z3 import *
x, y = Ints('x y')
solve(3 * x - 2 * y == 1, y - x == 1)

# Output: [x = 3, y = 4]

solve is shorthand for the check and model we were using above.

12.3 Solving Puzzles with SMT🔗

SMT solvers are useful for more than finding solutions to a random set of equations – you just have to know how to encode your problem in a form that the SMT solver understands. Here are three examples of puzzles that an SMT solver can solve. Next time you’re working on a puzzle, ask yourself whether it could be solved using SMT.

Often, SMT solvers are not used to find a solution, but to *prove that no solution exists*. For instance, say that we want to prove the mathematical fact y > 0 ==> x + y > x. To do this, we can ask the SMT solver if it ever the case that this is not true.


x, y = Ints('x y')
solve(Not(Implies(y > 0, x + y > x)))

# Output: no solution

The output here says that it is never not the case that y > 0 ==> x + y > x (a double negative). In other words: this formula is true for any choice of x and y!

12.4 Rabbits and Chickens🔗

Uncle Henry has 48 rabbits and chickens. He knows his rabbits and chickens have 108 legs, but does not know the exact number of rabbits and chickens. Can you help him? How many rabbits and chickens does Uncle Henry have?


#Create 2 integer variables
rabbit, chicken = Ints('rabbit chicken')
s = Solver()
s.add(rabbit + chicken == 48) # 48 animals
s.add(4 * rabbit + 2 * chicken == 108) # 108 legs
s.check() # solve the constraints
s.model() # get the solution

12.5 Cats and Dogs🔗

Say that you want to spend exactly 100 dollars to buy exactly 100 animals. Dogs cost 15 dollars, cats cost 1 dollar, and mice cost 25 cents each. You have to buy at least one of each. How many of each should you buy? Solution from


# Create 3 integer variables
dog, cat, mouse = Ints('dog cat mouse')

solve(dog >= 1,                   # at least one dog
      cat >= 1,                   # at least one cat
      mouse >= 1,                 # at least one mouse
      dog + cat + mouse == 100,   # 100 animals total
      # We have 100 dollars (10000 cents):
      #   dogs cost 15 dollars (1500 cents), 
      #   cats cost 1 dollar (100 cents), and 
      #   mice cost 25 cents 
      1500 * dog + 100 * cat + 25 * mouse == 10000)

12.6 Sudoku🔗

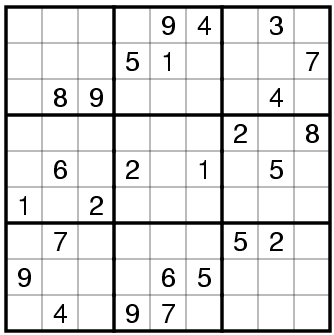
Sudoku is a puzzle where the goal is to insert numbers in boxes to satisfy the following condition: each row, column, and 3x3 box must contain the digits 1 through 9 exactly once.

The solution for the puzzle shown below. You can run it with ‘python3 sudoku.py‘.


from z3 import *

# 9x9 matrix of integer variables
X = [ [ Int("x_%s_%s" % (i+1, j+1)) for j in range(9) ]
      for i in range(9) ]

# each cell contains a value in {1, ..., 9}
cells_c  = [ And(1 <= X[i][j], X[i][j] <= 9)
             for i in range(9) for j in range(9) ]

# each row contains a digit at most once
rows_c   = [ Distinct(X[i]) for i in range(9) ]

# each column contains a digit at most once
cols_c   = [ Distinct([ X[i][j] for i in range(9) ])
             for j in range(9) ]

# each 3x3 square contains a digit at most once
sq_c     = [ Distinct([ X[3*i0 + i][3*j0 + j]
                        for i in range(3) for j in range(3) ])
             for i0 in range(3) for j0 in range(3) ]

sudoku_c = cells_c + rows_c + cols_c + sq_c

# sudoku instance, we use '0' for empty cells
instance = ((0,0,0,0,9,4,0,3,0),
            (0,0,0,5,1,0,0,0,7),
            (0,8,9,0,0,0,0,4,0),
            (0,0,0,0,0,0,2,0,8),
            (0,6,0,2,0,1,0,5,0),
            (1,0,2,0,0,0,0,0,0),
            (0,7,0,0,0,0,5,2,0),
            (9,0,0,0,6,5,0,0,0),
            (0,4,0,9,7,0,0,0,0))

instance_c = [ If(instance[i][j] == 0,
                  True,
                  X[i][j] == instance[i][j])
               for i in range(9) for j in range(9) ]

s = Solver()
s.add(sudoku_c + instance_c)
if s.check() == sat:
    m = s.model()
    r = [ [ m.evaluate(X[i][j]) for j in range(9) ]
          for i in range(9) ]
    print_matrix(r)
else:
    print("failed to solve")

12.7 Sum of Two Real Numers🔗

The sum of two nonzero real numbers is 4 times their product. What is the sum of the reciprocals of the two numbers? We’re going to solve this over real numbers:


from z3 import *
x, y = Reals('x y') 
s=Solver() 
s.add(x != 0)
s.add(y != 0) 
s.add(x + y == 4 * x * y)
print (s.check())
m=s.model()
print ("the model:", m)
print ("the answer:",m.evaluate (1/x + 1/y))
# 1/x + 1/y = (x+y)/ (x * y) == 4
#Instead of pulling values from the model and then 
# compute the final result on Python’s side, 
# we can evaluate an expression ( x1 + y1 ) inside the model we’ve got:
#sat
#the model:
#[x = 1, y = 1/3] 
#the answer: 4

12.8 Coin Sum🔗

Euler 31: “Coin sums” problem is as follows: In the United Kingdom the currency is made up of pound (£) and pence (p). There are eight coins in general circulation: 1p, 2p, 5p, 10p, 20p, 50p, £1 (100p), and £2 (200p). It is possible to make £2 in the following way:

1×£1 + 1×50p + 2×20p + 1×5p + 1×2p + 3×1p

How many different ways can £2 be made using any number of coins?


from z3 import *
a,b,c,d,e,f,g,h = Ints('a b c d e f g h')
s = Solver()
s.add(1*a + 2*b + 5*c + 10*d + 20*e + 50*f + 100*g + 200*h == 200,
      a>=0, b>=0, c>=0, d>=0, e>=0, f>=0, g>=0, h>=0) 
result =[]
while True:
    if s.check() == sat:
        m = s.model()
        print (m)
        result.append(m)
        # Create a new constraint the blocks the current model 
        block = []
        for d in m:
            # create a constant from declaration
            c=d()
            block.append(c != m[d]) 
        s.add(Or (block))
    else:
        print (len(result))
        break

12.9 8 Queens Puzzle🔗

The 8-Queens problem asks: given an 8×8 chessboard, place 8 queens on the board so that no two queens attack each other.


from z3 import *
N = 8

def var(row, col):
    return Int(f'cell_{row}_{col}')


vs = [ [ var(row, col) for col in range(N) ] for row in range(N) ]
cells_defined = [
      And(0 <= vs[i][j], vs[i][j] <= 1)
      for i in range(N) for j in range(N)
    ]
s = Solver()
s.add(cells_defined)
rows_ok = [Sum(vs[i]) == 1 for i in range(N)]

# all entries within a column must be distinct
cols_ok = [Sum([vs[i][j] for i in range(N)]) == 1 for j in range(N) ]

diagonals_ok = [Implies( And(vs[i][j] == 1, vs[k][h] == 1, 
                i != k, j != h), abs(k - i) != abs(j - h))
    for i in range(N) for j in range(N) 
    for k in range(N) for h in range(N)]

s.add(rows_ok)
s.add(cols_ok)
s.add(diagonals_ok)
if s.check() == sat:
    m = s.model()
    for i in range(N):
        for j in range(N):
            if m[var(i,j)] == 1:
                print(m[var(i,j)],end ="|")
            else:
                print(" ",end ="|")
        print("
---------------")
else:
    print("unsat")

12.10 Circle, Square, and Triangle🔗


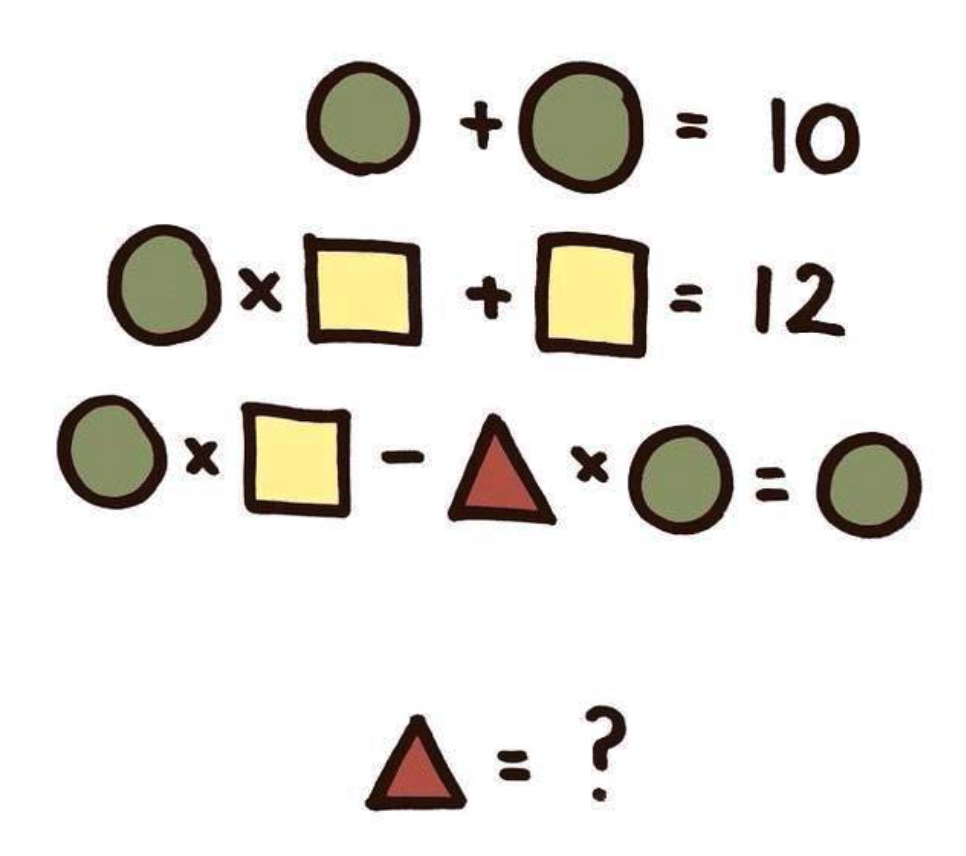
# circle + circle = 10
# circle * square + sqaure = 12
# circle * square - triangle * circle = circle
# What is th evalue of the triangle?


#!/ usr/bin/ python
from z3 import *
circle , square , triangle = Ints('circle square triangle')
s = Solver()
s.add( circle + circle ==10)
s.add( circle * square + square ==12)
s.add( circle *square - triangle * circle == circle )
if s.check() == unsat:
    print("UNSAT")
else:
    print (s.model())

12.11 De Morgan’s laws🔗

We want to prove

We will prove it by showing there is no falsifying interpertation of the formula.


from z3 import *
p, q = Bools('p q')
demorgan = And(p, q) == Not(Or(Not(p), Not(q)))
print (demorgan)

def prove(f):
    s = Solver()
    s.add(Not(f))
    if s.check() == unsat:
        print ("proved")
    else:
        print ("failed to prove")

print ("Proving demorgan...")
prove(demorgan)

12.12 Integer Overflow🔗

When a 16-bit vector is used, any integer greater than 2^16 - 1 = 65,535 will cause BV2Int to overflow. In the example below, if the sum of x and y exceeds 65,535, then BV2Int(x) + BV2Int(y) will not be equal to BV2Int(x + y).


from z3 import *
x = BitVec('x', 16)
y = BitVec('y', 16)
s = Solver()
s.add((BV2Int(x) + BV2Int(y)) != BV2Int(x+y))
if s.check()== sat:
    print(s.model())
else:
    print("unsat")

solve(BV2Int(x)+1 != BV2Int(x+1))

12.13 Wedding Seating🔗

Encode the placement of wedding guests in Z3.

Alice does not sit next to Charlie
Alice does not sit on the leftmost chair
Bob does not sit to the right of Charlie
Each person gets a chair
Every person gets at most one chair
Every chair gets at most one person

We will model assignment via nine boolean variables xpc, meaning the person p sits in chair c. Here are the constraints:

xal or xar implies not xcm: if Alice sits on the left or right, Charlie cannot sit in the middle.
xam implies not xcl and xcr: if Alice sits on the middle, Charlie cannot sit in the left or right.
not xal: Alice cannot sit on the leftmost chair
xcl ==> not xbm: If Charlie sits on left, Bob cannot sit in middle
xcm ==> not xbr: If Charlie sits on middle, Bob cannot sit in right


from z3 import *
xal, xam, xar, xbl, xbm, xbr, xcl, xcm, xcr = 
     Bools('xal xam xar xbl xbm xbr xcl xcm xcr')
s = Solver()
# Alice does not sit next to Charlie
s.add(And(Implies(Or(xal, xar), Not(xcm) ), 
       Implies(xam, And(Not(xcl), Not(xcr)))))
# Alice does not sit on the leftmost chair
s.add(Not(xal) )
# Bob does not sit to the right of Charlie
#s.add(And( Implies(xcl, Not(xbm)), Implies(xcm, Not(xbr))))

#Each person gets a chair
s.add( Or( xal, xam, xar) )
s.add( Or( xbl, xbm, xbr) )
s.add( Or( xcl, xcm, xcr) )

#Every person gets at most one chair
s.add( Or( Not(xal), Not(xam) ) )
s.add( Or( Not(xal), Not(xar) ) )
s.add( Or( Not(xam), Not(xar) ) )

#analogous for persons b and c
s.add( Or( Not(xbl), Not(xbm) ) )
s.add( Or( Not(xbl), Not(xbr) ) )
s.add( Or( Not(xbm), Not(xbr) ) )

s.add( Or( Not(xcl), Not(xcm) ) )
s.add( Or( Not(xcl), Not(xcr) ) )
s.add( Or( Not(xcm), Not(xcr) ) )


# Every chair gets at most one person
s.add( Or( Not(xal), Not(xbl) ) )
s.add( Or( Not(xal), Not(xcl) ) )
s.add( Or( Not(xbl), Not(xcl) ) )
# analogous for chairs m and r

s.add( Or( Not(xam), Not(xbm) ) )
s.add( Or( Not(xam), Not(xcm) ) )
s.add( Or( Not(xbm), Not(xcm) ) )

s.add( Or( Not(xar), Not(xbr) ) )
s.add( Or( Not(xar), Not(xcr) ) )
s.add( Or( Not(xbr), Not(xcr) ) )

if s.check() == sat:
    print(s.model())
else:
    print("UNSAT")

12.14 Magic Square🔗

A magic square is a square grid of numbers arranged so that the sum of the numbers in each row, each column, and both main diagonals is the same. This shared value is called the magic constant. The most common form, known as a normal magic square, uses consecutive integers from 1 to n² (where n is the size of the grid), and its magic constant is n × (n² + 1) ⁄ 2.


import os
import sys
from z3 import *
N = 7

S = N * (N * N +1)/2

def var(row, col):
    return Int(f'cell_{row}_{col}')

vs = [ [var(row,col) for col in range(N) ] for row in range(N) ]

cells_defined = [
      And(1 <= vs[i][j], vs[i][j] <= N * N)
      for i in range(N) for j in range(N)
    ]
s = Solver()
s.add(cells_defined)

rows_ok = [Sum(vs[i]) == S for i in range(N)]

cols_ok = [Sum([vs[i][j] for i in range(N)]) == S for j in range(N) ]

diagonals_ok1 = [Sum([vs[i][i] for i in range(N)]) == S]

diagonals_ok2 = [Sum([vs[i][N-i-1] for i in range(N)]) == S]

s.add(rows_ok)
s.add(cols_ok)
s.add(diagonals_ok1)
s.add(diagonals_ok2)

s.add(Distinct ([vs[i][j] for i in range(N) for j in range(N)]))

if s.check() == sat:
    m = s.model()
    for i in range(N):
        for j in range(N):
            print(m[var(i,j)],end ="|")
        print("
---------------")
else:
    print("unsat")

N = 3, Sum = 15

2	7	6
9	5	1
4	3	8

N = 5, Sum = 65

4	11	7	24	19
6	23	15	8	13
22	2	17	10	14
21	9	1	18	16
12	20	25	5	3

12.15 Limitations of the SMT Solvers🔗

SMT (Satisfiability Modulo Theories) solvers are powerful automated reasoning tools, but they do have several fundamental and practical limitations. Here’s a clear breakdown:

Theoretical Limitations
- Undecidability: SMT solvers extend SAT solving by reasoning about richer mathematical theories (e.g., arithmetic, arrays, bitvectors, datatypes). Some of these theories, or their combinations, are undecidable — meaning no algorithm can decide all possible formulas in them. Example: Nonlinear integer arithmetic (with multiplication of variables) is undecidable. Solvers use heuristics or incomplete methods for such cases.
- Incompleteness: For undecidable or very expressive theories, solvers cannot guarantee a result (“unknown”). This happens because they might only handle a decidable subset or stop after reaching resource limits.
Practical Limitations
- Scalability: As formulas grow larger and more complex, solving time can explode exponentially. SMT solvers struggle with formulas having: Many quantifiers (e.g., ∀, ∃), Nonlinear arithmetic, Deeply nested data structures or functions. This limits their use in large-scale software verification or complex symbolic execution.
- Quantifier Handling: SMT solvers are very efficient for quantifier-free formulas. Once quantifiers appear, they often rely on instantiation heuristics or E-matching, which are not guaranteed to find proofs or models. Example: Proving ∀x. ∃y. f(x, y) > 0 is very difficult automatically.
- Combining Theories: SMT solvers combine multiple theories (e.g., arrays + integers + bitvectors). While the Nelson–Oppen framework helps combine disjoint theories, interacting or overlapping theories (like arrays of integers with arithmetic constraints) are much harder.
Heuristic Nature: Many SMT procedures depend on heuristics (e.g., for branching, simplification, or lemma generation). This means: The same problem can take seconds or hours depending on formulation. Minor syntactic changes may drastically affect performance.
Model and Proof Limitations: Solvers typically return models (satisfying assignments), but: Models may be partial or approximate for complex types. Proof generation (for UNSAT cases) can be very large or not supported for all theories. This complicates proof checking and integration with theorem provers.
Limited Expressiveness for Some Tasks: SMT solvers are first-order — they cannot directly reason about higher-order functions, recursion, or induction (without encoding tricks). Proving properties about all programs or data structures inductively often requires integration with higher-level tools (like Dafny, Coq, or Isabelle).

Summary Table

Limitation Type	Description	Example
Undecidability	Some theories cannot be fully solved	Nonlinear integer arithmetic
Incompleteness	Solver may return “unknown”	Quantified formulas
Scalability	Performance drops for large/complex problems	Symbolic execution of large programs
Quantifiers	Poor handling of ∀ and ∃	Program verification
Theory combination	Hard to mix overlapping theories	Arrays + arithmetic
Heuristic behavior	Unpredictable performance	Minor changes cause slowdowns
Limited expressiveness	No direct induction or higher-order logic	Recursive properties

contents ← prev up next →

	Syllabus
	Texts
	Schedule
	Notes
	Assignments
	Midterms
	Final
	Software

1	Dafny Cheatsheet
2	Dafny Basics
3	Getting Started with Dafny
4	Dafny Collections
5	Floyd Hoare Logic
6	Inductive Proofs
7	Inductive Types
8	Sorting
9	Loop Invariants
10	Arrays
11	SAT Solvers
12	Solving SAT and SMT Problems Using Z3
13	Symbolic Execution
14	Testing
15	Functional Programming in Rocq
16	Logic in Rocq

12.1	Review of Logical Operators
12.2	SAT & SMT
12.3	Solving Puzzles with SMT
12.4	Rabbits and Chickens
12.5	Cats and Dogs
12.6	Sudoku
12.7	Sum of Two Real Numers
12.8	Coin Sum
12.9	8 Queens Puzzle
12.10	Circle, Square, and Triangle
12.11	De Morgan’s laws
12.12	Integer Overflow
12.13	Wedding Seating
12.14	Magic Square
12.15	Limitations of the SMT Solvers