Projects are listed by Type:
Algorithms, Machine Learning-AI, Quantum Computing
Notes: (1)These areas are not really disjoint. One of the Quantum projects using Machine Learnig. One of the ML-AI projects uses Algorithms. So they partition is an approximation. (2) If you click on the mentors name you get their website.
Algorithms Projects
TITLE: Parallel Algorithms for Nearest Neighbor Search
Mentor: Laxman Dhulipala, Tobias Rubel
Prerequisites Algorithms, experience with systems programming e.g., in C/C++, and interest in writing fast and highly scalable code on multicore CPUs (No need to have taken a parallel algorithms course)
Description
The Nearest Neighbor Problem is to design a data structure for a large set S of points in (say) n-dimensional space such that the following problem can be solved quickly: given a point p in n-dim space, find the point in S that is closest to p. The main concerns are that the data structure not take to much space, and that the nearest-neighbor query be fast.
We vary this problem in two ways: (1) rather than search for the nearest neighbor we will settle for an Approximate Nearest Neighbor ANN, (2) the algorithm that finds the ANN is a parallel algorithm.
One application of ANN is that n-dim datasets are becoming omnipresent due to the widespread adoption of deep learning methods which represent complex objects as high-dime vectors called vector embeddings, which can span thousands of dimensions.
The work will involve a mix of algorithm design, writing parallel code in C, and benchmarking implementations on large billion-point datasets.
TITLE: Exploring the Hilbert Geometry
Mentors: David Mount, Auguste Gezalyan
Prerequisites Knowledge of discrete structures/introduction to proofs, algorithms, and programming skills.
Description
The field of computational geometry looks at problems in Eucildian Geometry computationally. For example, given n points in the plane, find which two are closest together. But there are other metrics that have been useful in fields such as Genetics, Probability, and Physics (see HERE). In this project we will be examining the Hilbert Metric (see HERE) from the perspective of computational geometry. We will explore questions involving this metric, such as how it behaves in the probability simplex. (see HERE). The project will include contributing to a software package to help us visualize these structures. In this project you will learn computational geometry and combine computational geometry with programming.
Machine Learning and AI Projects
TITLE: What Makes Multimodal Question Answering Difficult?
Mentors: Jordan Boyd-Graber, Tasmin Kabir
Prerequisites Any one of the following:
1) Experience with calling Pytorch modules in Python (training is a plus), or
2) Building web apps connected to Python backend, or
3) Writing linguistically challenging / information rich examples for humans or computers
Description
New AI models are getting better at answering questions not just from text, but other modalities (image video sound) lag behind. However, these models still fall short. We are not sure where the difficulty currently lies. Here are possible answers in the form of questions:
(a) Can models not attend to the appropriate multimodal inputs?
(b) Is the training data insufficient?
(c) Is the alignment between modalities falling short?
In this project, we'll use existing algorithms on datasets and apply explanation methods to see where they fall short, construct / harvest examples that challenge the methods, and prepare a new challenge dataset for new methods to evaluate multimodal QA.
This will not just help us understand the limits of AI and help us improve systems understanding across modalities but also help people find information even when they cannot hear or see (either because of permanent or situational disability).
TITLE: Crop Planning Decision Support with Multi-Agent Reinforcement Learning
Mentor: Aviva Prins
Prereqisites Algorithms, Machine Learning, Python. Helpful but not required: Game theory, Databases (SQL)
Description
In India, the majority of farmers are classified as small or marginal, and their livelihoods are vulnerable to climate risk. Giving farmers help in planning crops well (e.g., delaying planting by a couple of days) can make a huge difference to their expected income. The overall goal of this project is to build an optimization-based decision support tool that provides crop planning advice to farmers.
Farmer features are very similar to each other, so they will get similar recommendations. However, the wholesale price of produce in India is very sensitive to supply-demand imbalances. If everyone plants the same thing, no one will profit. This summer, we'll be focusing on decision support for multiple farmers.
This work is in conjunction with Kheyti a nonprofit in India. Check out the paper that came out of last year's REU here.
Quantum Computing Projects
TITLE: Classical and Quantum Error Correction
Mentors: Victor Albert, Nat Tantivasadakarn
Prerequisites Linear Algebra, Quantum Mechanics, Quantum Computing, Quantum Error Correction (Two of the three Quantum Prerequisites may suffice)
Description
Error correction is what ensures that the audio in your phone calls remains sharp, your hard drives do not deteriorate too quickly, and signals can be reliably transmitted to remote satellites.
Over multiple decades, and with the explosion of the information age, an enormous variety of error-correction schemes were developed. Recently, a radically new type of error correction was introduced, one that can protect the quantum information that is stored in a quantum computer or that is communicated over a quantum network.
We created the Error Correction Zoo (see here) to categorize and to organize known classical and quantum error-correction schemes. It is inspired by other similar zoos, including the complexity zoo, the quantum algorithm zoo, the quantum protocol zoo, and the qubit zoo.
In this summer project, students will learn both classical and quantum error correction and contribute entries to the zoo's repository. The project can be scaled. On the easy end, there are tables and other readymade info to enter. On the hard end, the students can learn and write about advanced topics such as topological codes (see topological) and approximate quantum error correction (see approximate).
TITLE: Quantum Graph Games
Mentors: Seyed Sajjad Nezhadi, Jon Nelson
Prerequisites Linear Algebra, Graph Theory Basics, Quantum Information Theory Basics
Consider the following classical game with cooperating players Alice and Bob who do not communicate. There are two graphs G and H. A vertex sampler picks two random vertices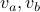 
of G and sends 
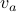to Alice and 
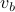to Bob. Alice and Bob respond with vertices 
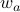and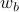 
of H. If the edge status 
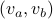in G and 
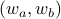in H are the same then Alice and Bob win, else they lose.
It is not hard to show that Alice and Bob can win iff there exists a homomorphism between G and H.
We consider a quantum version of this game. Which meens that Alice and Bob are allowed to share entangled quantum states and use them as part of their strategy to win the game. If the players can win these games we would call the two graphs quantum homomorphic.
Quantum homomorphisms are very well studied in the quantum graph theory literature and leads to quantum graph parameters such as quantum independence and quantum chromatic number (see CNMN+06 and PSS+16 below).
In this project we will look to study other graph properties related to or derived from graph homomorphisms in this quantum setting, such as induced subgraph isomorphism or weak homomorphisms, and try to relate them to other quantum and classic properties of graphs.
CMN+06 Peter J. Cameron, Ashley Montanaro, Michael W. Newman, Simone Severini, and Andreas Winter. On the quantum chromatic number of a graph, 2006. LINK
PSS+16 Vern I. Paulsen, Simone Severini, Daniel Stahlke, Ivan G. Todorov, and Andreas Winter. Estimating quantum chromatic numbers. Journal of Functional Analysis, 270(6):2188–2222, mar 2016. LINK
TITLE: Computing Error Bounds for Quantum Simulation Algorithms.
Mentors
Prerequisites Linear Algebra, Quantum Computing Basics
Simulating quantum mechanics is likely to be a major application of quantum computers. Some of the most effective quantum algorithms for simulating quantum dynamics on quantum computers are based on product formulas, which approximate the evolution according to a given Hamiltonian as a product of evolutions of its elementary terms. Recent work has provided good theoretical bounds on the quality of such approximations, but these bounds can be difficult to compute in practice, especially for high-order simulations of complicated quantum systems. This project will develop theoretical and computational methods for calculating product formula error bounds and implement them in software that can be used to understand resource requirements for practical quantum simulation.