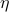Our results (some are already known)

Our Results of which some are known

nathan

Survey with no proofs

When Ramsey Theory Fails …

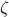Z

Countable Ordinals and big Ramsey Degrees by Masulovic and Sobot HERE

They prove 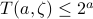. We have easier proof in our ordinal paper.

Some Partition Theorems and Ultrafilters on Omega PhD by Denis Devlin HERE

This contains much about 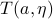. It cites Galvin (unpublished) 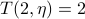but this is unpublished. I can't tell if it has the exact formula for .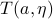

A proof of a partition theorem for by Vojan Vuksanovic HERE

Easier proof of the main theorems in Devlin's thesis. It does have the exact formula for 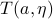, though I do not know if Devlin also did that.

A Useful Lemma

A partition theorem by Halpern and Lauchli. HERE

This paper proves a Ramsey Theorem on trees that is NOT about Ramsey Degrees but is used in many later papers. The proof is difficult. There are easier proofs in the following sources:

Introduction to Ramsey Spaces by Todorcevic HERE

Ramsey Theory for Product Spaces by Dodosa and Kanellopoulos. HERE

Some Appliations of Forcing by Todorceic and Farah. (This is a book that is not online.)

Ordinals

Countable Ordinals and big Ramsey Degrees by Masulovic and Sobot HERE

Let 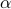be a countable ordinal. They show: 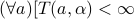is IFF .

Scattered Linear Orderings

Big Ramsey Spectra of Countable Chains by Masulovi. HERE

Let 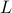be a Scattered Linear Order.

An Order Type Decomposition Theorem by Richard Laver HERE .

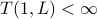Big Ramsey Spectra of countable chains by Dragan Masulovic HERE

If 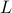has finite Hasudroff rank and bounded finite sums then .

If 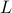has infinite Hasudroff rank then .

Rado and Similar Graphs

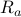is the Rado -ary Hypergraph.

The notion of finite Ramsey Degree is much more general here, looking at coloring finite substructures of the graph.

Edge Partitions of the Rado Graph by Pouzet and Sauer. HERE

They prove that for all finite colorings of the EDGES of the Rado graph 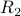there is an isomorphic copy of 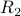which only uses 2 colors. We can cal this 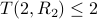. See next paper for .

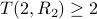Canonical Partitions of Universal Structures by Laflamme, Sauer, Vuksanovic HERE They show how to computer 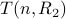exactly though do not give any numbers explicitly.

Counting Canonical Parttions in the Random Graph by Jean Larson HERE They give an algorithm to computer .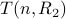

Strong Embeddings of Graphs into Colored Graphs By Erdos, Hajnal, Posa. HERE

Coloring Subgraphs of the Rado Graph by Sauer HERE They prove that there exists a finite coloring of the EDGES of the Rado graph 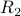such that any isomorphic copy of 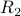uses 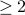colors.

Big Ramsey Degrees of 3-Uniform Hypergraphs are Finite by Balko, Chodounsky, Hubicka,Konecny, Vena HERE

They show that 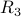has finite big Ramsey degree.

The Ramsey Theory of Henson Graphs by Dobrinen Here

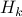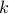The Henson graph is -clique free analogue of the Rado graph. This paper shows that 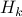has finite big Ramsey Degree.

Too hard for me

Big Ramsey Degree and Topological Dynamcs By Andy Zucker. HERE

Finite Big Ramsey Degree in Universal Structures By Masulovic HERE

Ramsey degrees of finite ultrametric spaces, ultrametric Urysohn spaces, and dynamics of their isometry groups By Lionel Nguyen Van The HERE

Big Ramsey Degrees using Paramter Spaces By Jan Hubicka HERE