Number Theory papers relevant to VDW theorem}
Consecutive nth powers
Definition
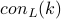 is the least prime such that for all
is the least prime such that for all
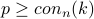 there will be
there will be  a run of
a run of  consecutive
consecutive
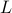 th powers.
End of Definition
th powers.
End of Definition
We abbreviate the phrase run of 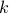 consecutive
consecutive 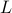 th powers by RkCL.
th powers by RkCL.
The following is in a paper by Lehmer and Lehmer (paper below) however, they seem to treat it as folklore.
Theorem 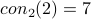 .
.
Proof
Note that there is no R2C2 mod 5.
Note that there is a R2C2 mod 7: 1,2 since 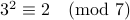 .
.
Let 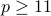 . All arithmetic is mod
. All arithmetic is mod 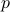 .
If 2 is a square then there is a pair, namely
.
If 2 is a square then there is a pair, namely 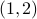 .
If 5 is a square then there is a pair, namely
.
If 5 is a square then there is a pair, namely 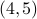 .
If neither is a square then the product
.
If neither is a square then the product 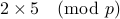 is a square and hence
is a square and hence
End of Proof
Note that this proof is elementary. More formally we
have a bound on where the R2C2 will be: it will always
start with a number that is 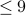 .
We call such proofs LL to honor Lehmer and Lehmer.
(Using the term elementary is not good since this
can mean other things.)
.
We call such proofs LL to honor Lehmer and Lehmer.
(Using the term elementary is not good since this
can mean other things.)
Many of the papers listed below show that this kind of proof
is not possible for some of the 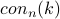 values.
values.
Papers about residues
H. Davenport.
On the distribution of quadratic residues mod p.
Journal of the London Mathematical Society, 6:49–54, 1932.
For 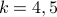 the number of RkC2 is
the number of RkC2 is 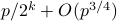 .
.
H. Davenport.
On the distribution of 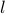 th power residues mod p.
Journal of the London Mathematical Society, 7:117–121, 1932.
HERE
The last theorem of this paper is that if
th power residues mod p.
Journal of the London Mathematical Society, 7:117–121, 1932.
HERE
The last theorem of this paper is that if 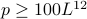 then there are 3 consecutive
then there are 3 consecutive
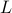 th roots mod
th roots mod 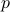 .
.
H. Davenport. On the distribution of quadratic residues mod p. Journal of the London Mathematical Society, 8:46–52, 1933. POINTER
D. Burgess.
The distribution of the quadratic residues and non-residues.
Mathematika, pages 106–112, 1957.
HERE
this paper shows that the max number of consecutive quadraic residues
or non-residues mod 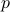 is
is 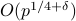 .
.
D. H. Lehmer and E. Lehmer.
On runs of residues.
Proceedings of the American Mathematical Society, 13:102–106,
1962.
This paper shows that there is no LL proof
of a bound on 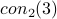 .
HERE
.
HERE
D. H. Lehmer, E. Lehmer, W. Mills, and J.L.Selfridge.
Machine proof of a theorem on cubic residues.
Mathematics of Computation, 16:407–415, 1962.
This paper gives an LL proof that 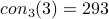 .
HERE
.
HERE
R. G. Bierstedy and W. H. Mills.
On the bound for a pair of consecutive quartic residues of a prime.
Proceedings of the American Mathematical Society, 14:628–632,
1963.
This paper gives an LL proof that 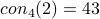 .
HERE
.
HERE
D. H. Lehmer and E. Lehmer.
On runs of residues.
Proceedings of the American Mathematical Society, 13:102–106,
1962.
D. H. Lehmer, E. Lehmer, and W. Mills.
Pairs of consecutive power residues.
Canadian Journal of Mathematics, 15:172–177, 1963.
This paper gives an LL proof that 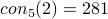 and
and
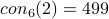 .
HERE
.
HERE
J. Brillhart, D. H. Lehmer, and E. Lehmer.
Bounds for pairs of consecutive seventh and higher powers.
Mathematics of Computation, 18:397–407, 1964.
This paper shows that if there is an LL proof for 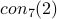 ,
(
,
(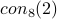 ,
, 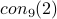 ,
, 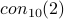 ) then the numbers involved
will be quite large (see the paper itself to make this formal).
HERE
) then the numbers involved
will be quite large (see the paper itself to make this formal).
HERE
R. Graham.
On quadruples of consecutive kth power residues.
Proceedings of the American Mathematical Society, 15:196–197,
1964.
1964. This paper show that, for all 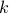 , there is NO LL proof
for
, there is NO LL proof
for 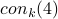 .
HERE
.
HERE
M. Dunton.
Bounds for pairs of cubic residues.
Proceedings of the American Mathematical Society, 16:330–332,
1965.
HERE
This paper gives an elementary proof that 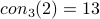 .
.
J. R. Rabung and J. H. Jordan.
Consecutive power residues or nonresidues.
Mathematics of Computation, 24:737–740, 1970.
url{http:www.jstor.orgstable2004850} or
url{http:www.cs.umd.edu gasarchres/}.
1970. This paper looks at the problem of finding a sequence
of 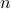 th powers OR non-
th powers OR non-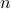 th powers.
HERE
th powers.
HERE
J. R. Rabung. On applications of van der {W}aerden's theorem. Mathematical Magazine, 48:142–148, 1975. HERE This paper looks at these kind of problems within the Gaussian Integers.
R. Peralta.
On the distribution of quadratic residues and nonresidues modulo a
prime number.
Mathematics of Computation, 58:433–440, 1992.
1992. This paper shows that 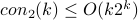 .
It is not stated that way.
HERE
.
It is not stated that way.
HERE
Papers about FLT
G. Libri. Me"moire sur la the"orie des nombres. Journal f{"{u}}r die reine und angewandte Mathematik, pages 54–81, 1832. HERE
P. Pepin. E'tude sur la the'orie des re'sidues cubiques. Journal de {Math'{e}matiques} Pures et {Appliqu'{e}es}, 2:313–324, 1876. HERE
P. Pepin. Sur divers tentatives de de'monstration du the'ore'me de {F}ermat. Comptes Rendus de l'Acad{'{e}}mie des Sciences Paris, HERE
A. E. Pellet. Me'morire sur la the'orie alge'brique des e'quations. Bulletin de la societe Mathematique de France, pages 61–103, 1887. HERE
L. E. Dickson. Lower limit for the number of sets of solutions of 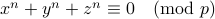 . Journal f{"{u}}r die reine und angewandte Mathematik, pages 181–189, 1909. HERE
. Journal f{"{u}}r die reine und angewandte Mathematik, pages 181–189, 1909. HERE
G. Cornacchia. Sulla congruenza 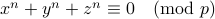 . Giornale di matematiche di Battaglini, pages 219–268, 1909. HERE
. Giornale di matematiche di Battaglini, pages 219–268, 1909. HERE
A. Hurwitz. U"ber die kongruenz 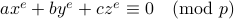 . Journal f{"{u}}r die reine und angewandte Mathematik, pages 272–292, 1909.
HERE
. Journal f{"{u}}r die reine und angewandte Mathematik, pages 272–292, 1909.
HERE