Overview
Deep neural networks are powerful machines for visual pattern recognition, but reasoning tasks that are easy for humans may still be difficult for neural models. Humans can extrapolate simple reasoning strategies to solve difficult problems using long sequences of abstract manipulations, i.e., harder problems are solved by thinking for longer. In contrast, the sequential computing budget of feed-forward networks is limited by their depth, and networks trained on simple problems have no way of extending their reasoning capabilities without retraining.
We propose “deep thinking” networks, which use recurrent modules to solve complex reasoning tasks. Because recurrent modules can be repeated as many times as desired during inference, we can increase the amount of cognitive effort used by the systems after training is complete. We observe that our thinking nets, when trained only on “easy” logical reasoning problem instances, can make a generalization leap to solve “hard” problems simply by increasing the number of recurrent iterations used at test time. In other words, thinking systems can solve problems of higher complexity simple by “thinking for longer.”
Our original paper on thinking systems:
Datasets
We have created pytorch data loaders for studying generalization from easy to hard problem instances. The generators can produce prefix sum, maze, and chess problem sets of various sizes and difficulties.
Datasets for Studying Generalization from Easy to Hard Examples
Example
One simple example of thinking systems is in solving mazes. When trained only on small 9x9 mazes, a classical feedforward network is not able to generalize to more complex mazes at test time. However, a thinking net can solve problems of seemingly arbitrary size after training only on 9x9 nets. To do this, the networks needs to perform more computations at test time by using more iterations of its recurrent unit.
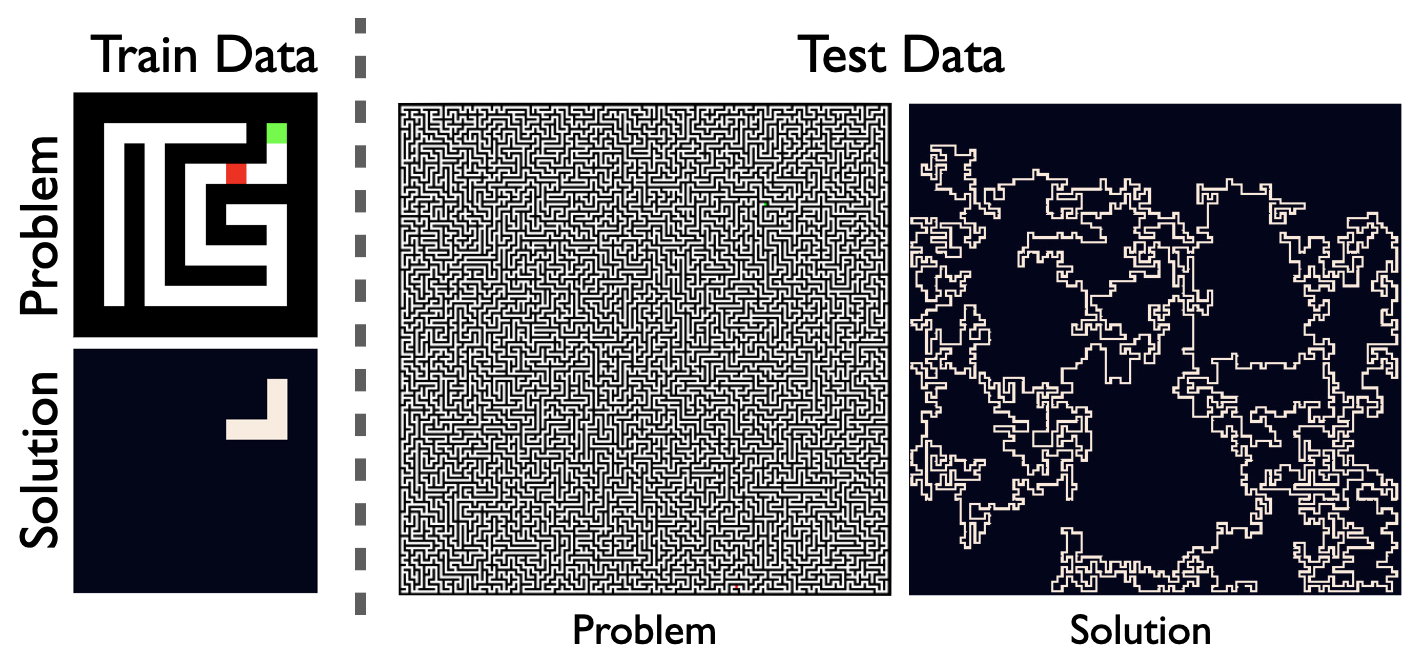
A Network trained only on 9x9 mazes can make a generalization leap to solve 201x201 (and larger) mazes at test time. However doing so requires orders of magnitude more computation.

