List of Projects
Explainable AI
Prerequisite: A background in artificial intelligence, data science, OR machine learning and an interest in human-computer interaction. Linear algebra also helpful.
With very little knowledge of machine learning, frameworks such as TensorFlow have made it easier than ever to quickly build, train, and deploy a neural network. However, this ease of use comes at a cost and sometimes errors in creating and training classifiers or constructing and tuning networks can result in mismatching of machine and human intelligence. Rookie mistakes combined with the opaque nature of modern neural networks can make it difficult to identify, let alone debug, problems in a machine intelligence model.
Our focus for the summer is on the developer: what are ways that we can provide insight at different phases of creating a neural network to improve the explainability and reliability of machine intelligence? This summer, we are focused on two main problem areas: 1) the construction and training of classifiers; and, 2) the design and tuning of a network.
Side Channels in the Cloud
According to the International Data Corporation (IDC), world wide spending on public cloud services will reach $127 billion by 2018. But public clouds give rise to unique security challenges, even when the cloud provider itself is trusted. In the course of this project we will explore these security challenges, focusing on the leakage of information during real-life computational tasks. Specifically, we will examine to what extent side-channel attacks can expose data when victim and spy processes are co-resident on the same physical machine.
Diversity in Matching Markets
Prerequisites: basic understanding of supervised machine learning, some experience with a programming language
How should a firm allocate its limited interviewing resources to select the optimal cohort of new employees from a large set of job applicants? How should that firm allocate cheap but noisy resume screenings and expensive but in-depth in-person interviews? We view this problem through the lens of combinatorial pure exploration (CPE) in the multi-armed bandit setting, where a central learning agent performs costly exploration of a set of arms before selecting a final subset with some combinatorial structure. In our case, that combinatorial structure will incorporate elements of diversity, where including multiple elements of the same type in the final set results in diminishing marginal gain. We will apply our algorithms to real data from university admissions and the hiring processes from major tech firms.
Knights, Knaves, and Hats
William Gasarch, Clyde Kruskal
Knights always tell the truth. Knaves always lie. Knights and Knaves have been a source of problems for many years (see the books of Raymond Smullyan). We have a possible new version. Let G be a graph on n vertices. Each vertex has a person on it who is a Knight or a Knave. You ask them all How many Knights do you see? Of course, the Knights will give a correct answer and the Knaves will give an incorrect answer. From this information can you figure out who is who?
A similar fun problem type are Hat Problems. We give one example and then talk about variants. There are n people who can all see each other. An adversary puts hats on their heads, on of n colors. Everyone can see everyone's hat except their own. They all, at the same time, shout out a color. If over 2/3 shout their own hat color they win! Otherwise they lose.
Variants include restricting who can see what, number of colors, adversary, hats put on randomly, and others. By one count there are 89,944 hat problems. See my blog post on hat problems.
Additionally, you can see a hat problem website.
Finding Colorings of the Plane Using Optimization Techniques
Thomas Goldstein, Clyde Kruskal
The following are known: For every 2-coloring of the plane there are two points an inch apart that are the same color. For every 3-coloring of the plane there are three points an inch apart that are the same color. There is a 7-coloring of the plane where all pairs of points that are in inch apart are different colors.
What happens for 4,5, and 6 colors? It is an open problem.
A region of the plane is c-colorable if you can color it with c colors and have no two points an inch apart be the same color. Tight bounds are known for coloring some types of regions, including circles and rectangles, with two and three colors. Little is known for more than three colors.
We look at the following: given a number c and a region of the plane, find if it is c-colorable. If it is then find the c-coloring.
While this is traditionally a pure math problem we will use optimization tools from applied math to color regions of the plane. We may also look at other conditions on colorings.
Modeling signals with deep neural networks
Prerequisite: Linear Algebra, Python. Helpful but not required: Maching Learning Toolboxes like PyTorch or TensorFlow.
Deep neural networks are a powerful tool for modeling images and text, but recent work has focused on methods for modeling signals. In this REU, we'll use methods from machine learning to model, analyze, and classify1-dimensional signals and time series data. One particular application of interest is modeling brain waves using data obtained via Magnetoencephalography (MEG) for the purpose of identifying seizures. We'll also investigate signals obtained from wireless communications, and time series data extracted from medical images and videos.
Cryptanalysis for Lattice-Based Cryptography
Prerequisites: Mathematical maturity and programming ability in C/C .
Knowledge of cryptography is useful but not essential.
.
Knowledge of cryptography is useful but not essential.
Next-generation cryptosystems may be based on newer assumptions related to the hardness of solving certain problems on lattices. This project will explore implementations of known algorithms from the literature for solving these problems in an effort to understand their concrete hardness.
Large Ind Sets OR Data Clustering
1) Implimenting graph approximation algorithms for a storage allocation problem.
This project entails implementing several heuristics for approximaion problems on graphs. Students need to be good coders and have a good understanding of graphs and their representations.
2) Clustering for fairness.
Given some data and some sensitive attributes like race, how can we find a fair clustering? In other words, each cluster should be well represetened racially. How can we design clustering algorithms to take this into account.
Trial and Error for Graph Properties
Prerquisite: Graph Theory
Algorithmic graph theory aims to characterize graphs based on their properties.
One of the ways this is done is by characterizing or testing when an unknown
graph 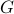 , accessed by querying an oracle, possesses a particular property.
Generally, the queries either ask if a particular edge is present in the
graph or the set of neighbours
for a particular vertex. In this project, for a property
, accessed by querying an oracle, possesses a particular property.
Generally, the queries either ask if a particular edge is present in the
graph or the set of neighbours
for a particular vertex. In this project, for a property 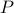 , we consider
more general queries in the form of certificates for
, we consider
more general queries in the form of certificates for 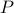 ( trials). The
oracle then reveals either that this certificate is indeed present in the
unknown graph or provides some information about some edge in the certificate
that is absent in
( trials). The
oracle then reveals either that this certificate is indeed present in the
unknown graph or provides some information about some edge in the certificate
that is absent in 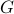 ( errors). This is essentially the graph property
framework of the trial and error model described in Ivanyos, et. al.
(IKQ+14 Ref Below)
For a particular kind of oracle in this framework, it is known that a property
( errors). This is essentially the graph property
framework of the trial and error model described in Ivanyos, et. al.
(IKQ+14 Ref Below)
For a particular kind of oracle in this framework, it is known that a property 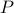 can be efficiently checked if there is an efficient algorithm for the associated
P^{cap} problem which asks: Given a graph H and a set of edges
can be efficiently checked if there is an efficient algorithm for the associated
P^{cap} problem which asks: Given a graph H and a set of edges
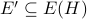 , is there a certificate for
, is there a certificate for 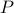 that contains an edge from
that contains an edge from 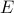 ’.
This raises the question of characterizing which properties
’.
This raises the question of characterizing which properties 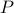 have polynomial time
algorithms for the associated
have polynomial time
algorithms for the associated 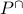 problem, which would be goal of this project.
This question would also hold interest independent of the trial and error model as a
means of finding a finer classification of poly-time solvable monotone graph properties.
problem, which would be goal of this project.
This question would also hold interest independent of the trial and error model as a
means of finding a finer classification of poly-time solvable monotone graph properties.
(IKQ+14) Gábor Ivanyos, Raghav Kulkarni, Youming Qiao, Miklos Santha, and Aarthi Sundaram. On the complexity of trial and error for constraint satisfaction problems. In Automata, Languages, and Programming - 41st International Colloquium, ICALP 2014, Copenhagen, Denmark, July 8-11, 2014, Proceedings, Part I, Lecture Notes in Computer Science, pages 663–675. Springer, 2014.” See here
Self-testing of Multi-Partite Quantum States with Marginal Correlations.
Prerequisite: Semidefinite Programming (theory and numeric), matrix analysis.
Self-testing is a device independent way to verify the state of a given quantum device and measurements associated to it. By device independent, it means that we do not assume the inner mechanism of the device and the dimension of the Hilbert space where the system lives. All the conclusions are made in a black-box fashion. Previous studies of self-testing require correlation functions involving all the parties in the system. In this project, we want to study the possibility of self-testing of certain multipartite quantum states which only require marginal, e.g., bipartite, correlation functions, which will considerably reduce the experimental efforts. A major part of the project is to conduct numerical analysis of semidefinite programs designed for self-testing of quantum states.