Projects
List of Projects
Sorting by Reversals
Andrew Childs, Aniruddha Bapat, Alexey Gorshkov, Eddie Schoute
In the Sorting By Reversals (SBR) problem, we wish to implement a given permutation using a minimum number of reversals. A reversal σ(i,j) inverts a subsequence as
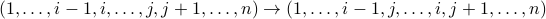
The SBR problem asks us to find the minimum number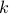 
of reversals 
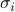, for ![iin [k]](eqs/2396769512763372931-130.png)
, such that
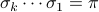. Caprara showed that SBR is NP-hard. (Other work even showed that it is
APX-hard,
which means hard to even approximate.) We now consider a variant of this problem where we are
allowed to do reversals on disjoint segments (i.e., ![[i,j]](eqs/1006117566228074858-130.png)
and ![[k,l]](eqs/3006127566244074854-130.png)
with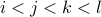 
)
in parallel and we wish to minimize the number of such parallel reversal steps.
This seems like a harder problem than SBR but its complexity is not known. In this project we will study the notion of “parallel sorting by reversals” and try to find and implement efficient algorithms for solving it. Furthermore, it would be interesting to prove hardness, and possibly the inapproximability, of this problem.
Diversity in Matching Markets
Prerequisites: Basic understanding of supervised machine learning, some experience with a programming language
How should a firm allocate its limited interviewing resources to select the optimal cohort of new employees from a large set of job applicants? How should that firm allocate cheap but noisy resume screenings and expensive but in-depth in-person interviews? We view this problem through the lens of combinatorial pure exploration (CPE) in the multi-armed bandit setting, where a central learning agent performs costly exploration of a set of arms before selecting a final subset with some combinatorial structure. In our case, that combinatorial structure will incorporate elements of diversity, where including multiple elements of the same type in the final set results in diminishing marginal gain. We will apply our algorithms to real data from university admissions and the hiring processes from major tech firms.
Using Generative Adversarial Networks to Guarantee Fairness
Prerequisite: Probability, Linear Algebra, Python programming preferred but not required.
Learning a probability model from data is a fundamental problem in machine learning and statistics. Building on the success of deep learning, there has been a modern approach to this problem using Generative Adversarial Networks (GANs). GANs view to this problem as a game between two sets of functions: a generator whose goal is to generate synthetic samples that are close to the real data training samples and a discriminator whose goal is to distinguish between the real and fake samples. In this project, we aim to leverage some of the state-of-the-art GAN architectures to produce distributions that are unbiased with respect to some protected features.
Machine Learning for Ramsey Games (not fun) and NIM with Cash (maybe fun)
William Gasarch and Joshua Twitty
Prerequisite: Mathematical maturity in linear Algebra, probability, statistics, exposure to Machine Learning is NOT required.
Consider the following game: RED and BLUE take turns coloring numbers RED and BLUE,
with RED going first. They are coloring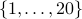 
. The first one to get an
arithmetic sequence of length 4 in their color wins! (A variant: loses!).
Does either player have a winning strategy? Can Machine Learning techniques help us
discern such a strategy? This is an example of a Ramsey Game. The origin of such
games is in a deep field of math called Ramsey Theory.
Throughout this project we will learn a variety of AI techniques for playing games: mini-max, alpha-beta, Deep Q-learning, monte carlo methods, and others. You will also learn Ramsey theory.
We may later apply AI techniques to variants of NIM, including NIM with Cash.
Generating Information From Neural Network Models
Prerequisite Some knowledge of Neural Nets
This project will explore ways to extract information from trained neural networks. We will explore this issue from two angles. First, we'll consider membership inference attacks, in which the attacker tries to extract information (images, private conversations, etc…) that were used to train a network. Our goal will be to develop new algorithms for executing such attacks, and also new algorithms for defending systems against such attacks. Second, we will view algorithms for reconstructing training images as a means for creating digital art and graphics.
Learning Fair Representations
Prerequisite: Mathematical maturity in linear Algebra, probability, statistics, exposure to Machine Learning is required.
Machine learning algorithms are very powerful and they are being used everywhere today. Unfortunately, machine learning algorithms can learn bias as they learn. This could have drastic consequences. Many concerns have been voiced about the susceptibility of data-intensive AI algorithms to error and misuse, and the possible ramifications for gender, age, racial, or economic classes. The proper collection and use of data for AI systems, in this regard, represent an important challenge. Beyond purely data-related issues, however, larger questions arise about the design of AI to be inherently just, fair, transparent, and accountable. Researchers must learn how to design these systems so that their actions and decision-making are transparent and easily interpretable by humans, and thus can be examined for any bias they may contain, rather than just learning and repeating these biases. There are serious intellectual issues about how to represent and ‘‘encode’’ value and belief systems. Scientists must also study to what extent justice and fairness considerations can be designed into the system, and how to accomplish this within the bounds of current engineering techniques.
The overall goal is to obtain a representation of our original data that has the same dimension as the original data, and preserves as much of information in the original data as possible while de-correlating the sensitive attribute.
Cryptanalysis for Lattice-Based Cryptography
Prerequisites: Mathematical maturity and programming ability in C/C
.
Knowledge of cryptography is useful but not essential.
Next-generation cryptosystems may be based on newer assumptions related to the hardness of solving certain problems on lattices. This project will explore implementations of known algorithms from the literature for solving these problems in an effort to understand their concrete hardness.