Publications
- A Scalable Open-Source QEC System with Sub-Microsecond Decoding-Feedback Latency
-
Manuscript, 2025.Links:Abstract:
Quantum error correction (QEC) is essential for realizing large-scale, fault-tolerant quantum computation, yet its practical implementation remains a major engineering challenge. In particular, QEC demands precise real-time control of a large number of qubits and low-latency, high-throughput and accurate decoding of error syndromes. While most prior work has focused primarily on decoder design, the overall performance of any QEC system depends critically on all its subsystems including control, communication, and decoding, as well as their integration.
To address this challenge, we present an open-source, fully integrated QEC system built on RISC-Q, a generator for RISC-V–based quantum control architectures. Implemented on RFSoC FPGAs, our system prototype integrates real-time qubit control, a scalable distributed multi-board architecture, and the state-of-the-art hardware QEC decoder within a low-latency, high-throughput decoding pipeline, forming a complete hardware platform ready for deployment with superconducting qubits.
Experimental evaluation on a three-board prototype based on AMD ZCU216 RFSoCs demonstrates an end-to-end QEC decoding-feedback latency of 446 ns for a distance-3 surface code, including syndrome aggregation, network communication, syndrome decoding, and error distribution. Extrapolating from measured subsystem performance and state-of-the-art decoder benchmarks, the architecture can achieve sub-microsecond decoding-feedback latency up to a distance-21 surface code (
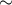 881 physical qubits) when scaled to larger hardware configurations.
881 physical qubits) when scaled to larger hardware configurations. - Optimal and Robust In-situ Quantum Hamiltonian Learning through Parallelization
-
Manuscript, 2025Links: arXiv:2510.07818Abstract:
Hamiltonian learning is a cornerstone for advancing accurate many-body simulations, improving quantum device performance, and enabling quantum-enhanced sensing. Existing readily deployable quantum metrology techniques primarily focus on achieving Heisenberg-limited precision in one- or two-qubit systems. In contrast, general Hamiltonian learning theories address broader classes of unknown Hamiltonian models but are highly inefficient due to the absence of prior knowledge about the Hamiltonian. There remains a lack of efficient and practically realizable Hamiltonian learning algorithms that directly exploit the known structure and prior information of the Hamiltonian, which are typically available for a given quantum computing platform. In this work, we present the first Hamiltonian learning algorithm that achieves both Cramer-Rao lower bound saturated optimal precision and robustness to realistic noise, while exploiting device structure for quadratic reduction in experimental cost for fully connected Hamiltonians. Moreover, this approach enables simultaneous in-situ estimation of all Hamiltonian parameters without requiring the decoupling of non-learnable interactions during the same experiment, thereby allowing comprehensive characterization of the system's intrinsic contextual errors. Notably, our algorithm does not require deep circuits and remains robust against both depolarizing noise and time-dependent coherent errors. We demonstrate its effectiveness with a detailed experimental proposal along with supporting numerical simulations on Rydberg atom quantum simulators, showcasing its potential for high-precision Hamiltonian learning in the NISQ era.
- RISC-Q: A Generator for Real-Time Quantum Control System-on-Chips Compatible with RISC-V
-
Manuscript, 2025Links: arXiv:2505.14902Abstract:
Quantum computing imposes stringent requirements for the precise control of large-scale qubit systems, including, for example, microsecond-latency feedback and nanosecond-precision timing of gigahertz signals – demands that far exceed the capabilities of conventional real-time systems. The rapidly evolving and highly diverse nature of quantum control necessitates the development of specialized hardware accelerators. While a few custom real-time systems have been developed to meet the tight timing constraints of specific quantum platforms, they face major challenges in scaling and adapting to increasingly complex control demands – largely due to fragmented toolchains and limited support for design automation.
To address these limitations, we present RISC-Q – an open-source flexible generator for Quantum Control System-on-Chip (QCSoC) designs, featuring a programming interface compatible with the RISC-V ecosystem. Developed using SpinalHDL, RISC-Q enables efficient automation of highly parameterized and modular QCSoC architectures, supporting agile and iterative development to meet the evolving demands of quantum control. We demonstrate that RISC-Q can replicate the performance of existing QCSoCs with significantly reduced development effort, facilitating efficient exploration of the hardware-software co-design space for rapid prototyping and customization.
- (Sub)Exponential Quantum Speedup for Optimization
-
Manuscript, 2025Links: arXiv:2504.14841Abstract:
We demonstrate provable (sub)exponential quantum speedups in both discrete and continuous optimization, achieved through simple and natural quantum optimization algorithms, namely the quantum adiabatic algorithm for discrete optimization and quantum Hamiltonian descent for continuous optimization. Our result builds on the Gilyén–Hastings–Vazirani (sub)exponential oracle separation for adiabatic quantum computing. With a sequence of perturbative reductions, we compile their construction into two standalone objective functions, whose oracles can be directly leveraged by the plain adiabatic evolution and Schrödinger operator evolution for discrete and continuous optimization, respectively.
- Quantum Hamiltonian Descent for Non-smooth Optimization
-
Manuscript, 2025Links: arXiv:2503.1587Abstract:
Non-smooth optimization models play a fundamental role in various disciplines, including engineering, science, management, and finance. However, classical algorithms for solving such models often struggle with convergence speed, scalability, and parameter tuning, particularly in high-dimensional and non-convex settings. In this paper, we explore how quantum mechanics can be leveraged to overcome these limitations. Specifically, we investigate the theoretical properties of the Quantum Hamiltonian Descent (QHD) algorithm for non-smooth optimization in both continuous and discrete time. First, we propose continuous-time variants of the general QHD algorithm and establish their global convergence and convergence rate for non-smooth convex and strongly convex problems through a novel Lyapunov function design. Furthermore, we prove the finite-time global convergence of continuous-time QHD for non-smooth non-convex problems under mild conditions (i.e., locally Lipschitz). In addition, we propose discrete-time QHD, a fully digitized implementation of QHD via operator splitting (i.e., product formula). We find that discrete-time QHD exhibits similar convergence properties even with large time steps. Finally, numerical experiments validate our theoretical findings and demonstrate the computational advantages of QHD over classical non-smooth non-convex optimization algorithms.
- Robust analog quantum simulators by quantum error-detecting codes
-
Manuscript, 2024Links: arXiv:2412.07764Abstract:
Achieving noise resilience is an outstanding challenge in Hamiltonian-based quantum computation. To this end, energy-gap protection provides a promising approach, where the desired quantum dynamics are encoded into the ground space of a penalty Hamiltonian that suppresses unwanted noise processes. However, existing approaches either explicitly require high-weight penalty terms that are not directly accessible in current hardware, or utilize non-commuting 2-local Hamiltonians, which typically leads to an exponentially small energy gap. In this work, we provide a general recipe for designing error-resilient Hamiltonian simulations, making use of an excited encoding subspace stabilized by solely 2-local commuting Hamiltonians. Our results thus overcome a no-go theorem previously derived for ground-space encoding that prevents noise suppression schemes with such Hamiltonians. Importantly, our method is scalable as it only requires penalty terms that scale polynomially with system size. To illustrate the utility of our approach, we further apply this method to a variety of 1D and 2D many-body spin models, potentially extending the duration of high-fidelity simulation by orders of magnitude in current hardware.
- On the Computational Complexity of Schrödinger Operators
-
Contributed Talk at QIP 2025.Links: arXiv:2411.05120Abstract:
We study computational problems related to the Schrödinger operator
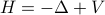 in the real space under the condition that (i) the potential function
in the real space under the condition that (i) the potential function 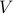 is smooth and has its value and derivative bounded within some polynomial of
is smooth and has its value and derivative bounded within some polynomial of 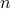 and (ii)
and (ii) 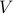 only consists of
only consists of 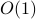 -body interactions.
We prove that (i) simulating the dynamics generated by the Schrödinger operator implements universal quantum computation, i.e., it is BQP-hard, and (ii) estimating the ground energy of the Schrödinger operator is as hard as estimating that of local Hamiltonians with no sign problem (a.k.a. stoquastic Hamiltonians), i.e., it is Stoq-MA-complete. This result is particularly intriguing because the ground energy problem for general bosonic Hamiltonians is known to be QMA-hard and it is widely believed that
Stoq-MA is a subset of QMA.
-body interactions.
We prove that (i) simulating the dynamics generated by the Schrödinger operator implements universal quantum computation, i.e., it is BQP-hard, and (ii) estimating the ground energy of the Schrödinger operator is as hard as estimating that of local Hamiltonians with no sign problem (a.k.a. stoquastic Hamiltonians), i.e., it is Stoq-MA-complete. This result is particularly intriguing because the ground energy problem for general bosonic Hamiltonians is known to be QMA-hard and it is widely believed that
Stoq-MA is a subset of QMA. - Differentiable Quantum Computing for Large-scale Linear Control
-
NeurIPS 2024.Links: arXiv:2411.01391Abstract:
As industrial models and designs grow increasingly complex, the demand for optimal control of large-scale dynamical systems has significantly increased. However, traditional methods for optimal control incur significant overhead as problem dimensions grow. In this paper, we introduce an end-to-end quantum algorithm for linear-quadratic control with provable speedups. Our algorithm, based on a policy gradient method, incorporates a novel quantum subroutine for solving the matrix Lyapunov equation. Specifically, we build a quantum-assisted differentiable simulator for efficient gradient estimation that is more accurate and robust than classical methods relying on stochastic approximation. Compared to the classical approaches, our method achieves a super-quadratic speedup. To the best of our knowledge, this is the first end-to-end quantum application to linear control problems with provable quantum advantage.
- Efficient Routing on Quantum Networks using Adaptive Clustering
-
In the Proceedings of the 32nd IEEE International Conference on Network Protocols (ICNP 2024).Links: arXiv:2410.23007Abstract:
We introduce QuARC, Quantum Adaptive Routing using Clusters, a novel clustering-based entanglement routing protocol that leverages redundant, multi-path routing through multi-particle projective quantum measurements to enable high-throughput, low-overhead, starvation-free entanglement distribution. At its core, QuARC periodically reconfigures the underlying quantum network into clusters of different sizes, where each cluster acts as a small network that distributes entanglement across itself, and the end-to-end entanglement is established by further distributing between clusters. QuARC does not require a-priori knowledge of any physical parameters, and is able to adapt the network configuration using static topology information, and using local (within-cluster) measurements only. We present a comprehensive simulation-based evaluation that shows QuARC is robust against changes to physical network parameters, and maintains high throughput without starvation even as network sizes scale and physical parameters degrade.
- QHDOPT: A Software for Nonlinear Optimization with Quantum Hamiltonian Decent
-
INFORMS Journal on Computing 37(1):107-124. GithubLinks: arXiv:2401.08550Abstract:
We develop an open-source, end-to-end software (named QHDOPT), which can solve nonlinear optimization problems using the quantum Hamiltonian descent (QHD) algorithm. QHDOPT offers an accessible interface and automatically maps tasks to various supported quantum backends (i.e., quantum hardware machines). These features enable users, even those without prior knowledge or experience in quantum computing, to utilize the power of existing quantum devices for large-scale nonlinear and nonconvex optimization tasks. In its intermediate compilation layer, QHDOPT employs SimuQ, an efficient interface for Hamiltonian-oriented programming, to facilitate multiple algorithmic specifications and ensure compatible cross-hardware deployment.
- Expanding Hardware-efficiently Manipulable Hilbert space by Hamiltonian Embedding
-
Quantum 9, 1857 (2025).Links: arXiv:2401.08550Abstract:
Many promising quantum applications depend on the efficient quantum simulation of an exponentially large sparse Hamiltonian, a task known as sparse Hamiltonian simulation, which is fundamentally important in quantum computation. Although several theoretically appealing quantum algorithms have been proposed for this task, they typically require a black-box query model of the sparse Hamiltonian, rendering them impractical for near-term implementation on quantum devices.
In this paper, we propose a technique named Hamiltonian embedding that simulates a desired Hamiltonian evolution by embedding it into the evolution of a large and structured quantum system, which, however, allows more efficient manipulation via hardware-native operations. We conduct a systematic study of this embedding technique and demonstrate a significant computational resource save for implementing prominent quantum applications. As a result, we can experimentally realize quantum walks on complicated graphs (e.g., binary trees, glued-tree graphs), quantum spatial search, and the simulation of real-space Schrödinger equations on trapped-ion and neutral-atom platforms today. Given the fundamental role of Hamiltonian evolution in quantum algorithm design, our technique significantly expands the horizon of implementable quantum advantage in the NISQ era.
- Microwave signal processing using an analog quantum reservoir computer
-
Nature Communication, 15, 7490 (2024).Links: arXiv:2312.16166Abstract:
Quantum reservoir computing (QRC) has been proposed as a paradigm for performing machine learning with quantum processors where the training is efficient in the number of required runs of the quantum processor and takes place in the classical domain, avoiding the issue of barren plateaus in parameterized-circuit quantum neural networks. It is natural to consider using a quantum processor based on superconducting circuits to classify microwave signals that are analog - continuous in time. However, while theoretical proposals of analog QRC exist, to date QRC has been implemented using circuit-model quantum systems – imposing a discretization of the incoming signal in time, with each time point input by executing a gate operation. In this paper we show how a quantum superconducting circuit comprising an oscillator coupled to a qubit can be used as an analog quantum reservoir for a variety of classification tasks, achieving high accuracy on all of them. Our quantum system was operated without artificially discretizing the input data, directly taking in microwave signals. Our work does not attempt to address the question of whether QRCs could provide a quantum computational advantage in classifying pre-recorded classical signals. However, beyond illustrating that sophisticated tasks can be performed with a modest-size quantum system and inexpensive training, our work opens up the possibility of achieving a different kind of advantage than a purely computational advantage: superconducting circuits can act as extremely sensitive detectors of microwave photons; our work demonstrates processing of ultra-low-power microwave signals in our superconducting circuit, and by combining sensitive detection with QRC processing within the same system, one could achieve a quantum sensing-computational advantage, i.e., an advantage in the overall analysis of microwave signals comprising just a few photons.
- A Quantum-Classical Performance Separation in Nonconvex Optimization
-
Manuscript 2023. Github.Links: arXiv:2311.00811Abstract:
In this paper, we identify a family of nonconvex continuous optimization instances, each
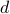 -dimensional instance with
-dimensional instance with 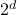 local minima, to demonstrate a quantum-classical performance separation. Specifically, we prove that the recently proposed Quantum Hamiltonian Descent (QHD) algorithm (Leng et al. arXiv:2303.01471) is able to solve any
local minima, to demonstrate a quantum-classical performance separation. Specifically, we prove that the recently proposed Quantum Hamiltonian Descent (QHD) algorithm (Leng et al. arXiv:2303.01471) is able to solve any 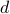 -dimensional instance from this family using
-dimensional instance from this family using  quantum queries to the function value and
quantum queries to the function value and 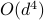 additional 1-qubit and 2-qubit elementary quantum gates. On the other side, a comprehensive empirical study suggests that representative state-of-the-art classical optimization algorithms/solvers (including Gurobi) would require a super-polynomial time to solve such optimization instances.
additional 1-qubit and 2-qubit elementary quantum gates. On the other side, a comprehensive empirical study suggests that representative state-of-the-art classical optimization algorithms/solvers (including Gurobi) would require a super-polynomial time to solve such optimization instances. - A quantum central path algorithm for linear optimization
-
Contributed Talk at QIP 2025.Links: arXiv:2311.03977Abstract:
We propose a novel quantum algorithm for solving linear optimization problems by quantum-mechanical simulation of the central path. While interior point methods follow the central path with an iterative algorithm that works with successive linearizations of the perturbed KKT conditions, we perform a single simulation working directly with the nonlinear complementarity equations. Combining our approach with iterative refinement techniques, we obtain an exact solution to a linear optimization problem involving
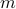 constraints and
constraints and 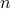 variables using at most
variables using at most 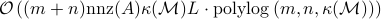 elementary gates and
elementary gates and 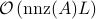 classical arithmetic operations, where
classical arithmetic operations, where 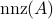 is the total number of non-zero elements found in the constraint matrix,
is the total number of non-zero elements found in the constraint matrix, 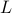 denotes binary input length of the problem data, and
denotes binary input length of the problem data, and 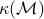 is a condition number that depends only on the problem data.
is a condition number that depends only on the problem data. - Fixing and Mechanizing the Security Proof of Fiat-Shamir with Aborts and Dilithium
-
CRYPTO 2023.Links: iacr-eprint-2023-246Abstract:
We extend and consolidate the security justification for the Dilithium signature scheme. In particular, we identify a subtle but crucial gap that appears in several ROM and QROM security proofs for signature schemes that are based on the Fiat-Shamir with aborts paradigm, including Dilithium. The gap lies in the CMA-to-NMA reduction and was uncovered when trying to formalize a variant of the QROM security proof by Kiltz, Lyubashevsky, and Schaffner (Eurocrypt 2018). The gap was confirmed by the authors, and there seems to be no simple patch for it. We provide new, fixed proofs for the affected CMA-to-NMA reduction, both for the ROM and the QROM, and we perform a concrete security analysis for the case of Dilithium to show that the claimed security level is still valid after addressing the gap. Furthermore, we offer a fully mechanized ROM proof for the CMA-security of Dilithium in the EasyCrypt proof assistant. Our formalization includes several new tools and techniques of independent interest for future formal verification results.
- Qafny: Quantum Program Verification Through Type-guided Classical Separation Logic
-
ECOOP 2024. GithubLinks: arXiv:2211.06411Abstract:
Formal verification has been proven instrumental to ensure that quantum programs implement their specifications but often requires a significant investment of time and labor. To address this challenge, we present Qafny, an automated proof system designed for verifying quantum programs. At its core, Qafny uses a type-guided quantum proof system that translates quantum operations to classical array operations. By modeling these operations as proof rules within a classical separation logic framework, Qafny provides automated support for the reasoning process that would otherwise be tedious and time-consuming. We prove the soundness and completeness of our proof system and implement a prototype compiler that transforms Qafny programs both into the Dafny programming language and into executable quantum circuits. Using Qafny, we demonstrate how to efficiently verify prominent quantum algorithms, including quantum-walk algorithms, Grover's search algorithm, and Shor's factoring algorithm, with significantly reduced human efforts.
- A Scalable Classical Verification reveals the Gap of the State-Of-The-Art Gaussian Boson Sampling Experiments
-
Manuscript, 2023.Abstract:
Gaussian Boson Sampling (GBS) is one major candidate for establishing quantum computational advantage in the near term. Despite promising experimental progress, most existing validation schemes of GBS experiments merely rule out a few experimentally-motivated alternative physical hypotheses and fail to certify the device’s output distribution directly, which is critical for establishing the computational hardness. Inspired by the symmetry property of Hafnian functions, we propose a scalable classical verification scheme of GBS, based on symmetry testing via a coarse-grained statistical heuristic, with strong theoretical and empirical evidence for its validity. Theoretically, when symmetry properties are approximately established, we prove that the device's output distribution is close to GBS under a mild assumption of the device. Empirically, based on classical simulation of up to 20 modes, we observe that our protocol can successfully distinguish GBS devices from all known alternative physical hypotheses and is further resilient to a small photon loss in the experiment. We perform part of our verification scheme on Xanadu’s Borealis machine, which reveals a large inhomogeneity among alleged 216 squeezed modes that fail our symmetry test, and hence a gap for the claimed computational advantage based on GBS.
- SimuQ: A Framework for Programming Quantum Hamiltonian Simulation with Analog Compilation
-
POPL 2024. WebsiteLinks: arXiv:2303.02775Abstract:
Quantum Hamiltonian simulation, which simulates the evolution of quantum systems and probes quantum phenomena, is one of the most promising applications of quantum computing. Recent experimental results suggest that Hamiltonian-oriented analog quantum simulation would be advantageous over circuit-oriented digital quantum simulation in the Noisy Intermediate-Scale Quantum (NISQ) machine era. However, programming analog quantum simulators is much more challenging due to the lack of a unified interface between hardware and software. In this paper, we design and implement SimuQ, the first framework for quantum Hamiltonian simulation that supports Hamiltonian programming and pulse-level compilation to heterogeneous analog quantum simulators. Specifically, in SimuQ, front-end users specify the target quantum system with Hamiltonian Modeling Language, and the Hamiltonian-level programmability of analog quantum simulators is specified through a new abstraction called the abstract analog instruction set (AAIS) and programmed in AAIS Specification Language by hardware providers. Through a solver-based compilation, SimuQ generates executable pulse schedules for real devices to simulate the evolution of desired quantum systems, which is demonstrated on superconducting (IBM), neutral-atom (QuEra), and trapped-ion (IonQ) quantum devices. Moreover, we demonstrate the advantages of exposing the Hamiltonian-level programmability of devices with native operations or interaction-based gates and establish a small benchmark of quantum simulation to evaluate SimuQ's compiler with the above analog quantum simulators.
- Distributed Quantum Sensing Network with Geographically Constrained Measurement Strategies
-
In the Proceedings of the 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2023).Abstract:
Distributed quantum sensing network has the potential of enhancing the precision in estimating a global function of local parameters by utilizing an entangled probe, compared with that achieved with separable probes. This advantage is often characterized as a quadratic improvement of the quantum Cramér-Rao bound (QCRB). This argument is incomplete in that QCRB assumes a team of all-powerful sensors that can perform arbitrary joint measurements allowed by quantum mechanics. An immediate question arises as to whether such an advantage persists for isolated sensors with physically motivated constraints in their measurement strategies. In this paper, we first consider local operations and classical communication (LOCC) strategies and prove that the QCRB is indeed asymptotically attainable for arbitrary pure probe states, by extending previous work on single-parameter estimation. We further numerically analyze a more restricted scenario where the sensors can only make independent local measurements, and provide evidence that the QCRB is not informative enough for comparing different probe states.
- A Case for Synthesis of Recursive Quantum Unitary Programs
-
POPL 2024. GithubLinks: arXiv:2311.11503Abstract:
Quantum programs are notoriously difficult to code and verify due to unintuitive quantum knowledge associated with quantum programming. Automated tools relieving the tedium and errors associated with low-level quantum details would hence be highly desirable. In this paper, we initiate the study of program synthesis for quantum unitary programs that recursively define a family of unitary circuits for different input sizes, which are widely used in existing quantum programming languages. Specifically, we present QSynth, the first quantum program synthesis framework, including a new inductive quantum programming language, its specification, a sound logic for reasoning, and an encoding of the reasoning procedure into SMT instances. By leveraging existing SMT solvers, QSynth successfully synthesizes ten quantum unitary programs including quantum adder circuits, quantum eigenvalue inversion circuits and Quantum Fourier Transformation, which can be readily transpiled to executable programs on major quantum platforms, e.g., Q
- Quantum Hamiltonian Descent
-
More information at the accompanying website.Links: arXiv:2303.01471Abstract:
Gradient descent is a fundamental algorithm in both theory and practice for continuous optimization. Identifying its quantum counterpart would be appealing to both theoretical and practical quantum applications. A conventional approach to quantum speedups in optimization relies on the quantum acceleration of intermediate steps of classical algorithms while keeping the overall algorithmic trajectory and solution quality unchanged. We propose Quantum Hamiltonian Descent (QHD), which is derived from the path integral of dynamical systems referring to the continuous-time limit of classical gradient descent algorithms, as a truly quantum counterpart of classical gradient methods where the contribution from classically-prohibited trajectories can significantly boost QHD’s performance for non-convex optimization. Moreover, QHD is described as a Hamiltonian evolution efficiently simulatable on both digital and analog quantum computers. By embedding QHD’s Hamiltonian evolution into the one of the so-called Quantum Ising Machine (including D-Wave and others), we empirically observe that the D-Wave-implemented QHD outperforms a selection of state-of-the-art gradient-based classical solvers and the standard quantum adiabatic algorithm, based on the time-to-solution metric, on non-convex constrained quadratic programming instances up to 75 dimensions. Finally, we propose a “three-phase picture” to explain the behavior of QHD, especially its difference from the quantum adiabatic algorithm.
- Analyzing Convergence in Quantum Neural Networks: Deviations from Neural Tangent Kernels
-
ICML 2023.Links: arXiv:2303.14844Abstract:
A quantum neural network (QNN) is a parameterized mapping efficiently implementable on near-term Noisy Intermediate-Scale Quantum (NISQ) computers. It can be used for supervised learning when combined with classical gradient-based optimizers. Despite the existing empirical and theoretical investigations, the convergence of QNN training is not fully understood. Inspired by the success of the neural tangent kernels (NTKs) in probing into the dynamics of classical neural networks, a recent line of works proposes to study over-parameterized QNNs by examining a quantum version of tangent kernels. In this work, we study the dynamics of QNNs and show that contrary to popular belief it is qualitatively different from that of any kernel regression: due to the unitarity of quantum operations, there is a non-negligible deviation from the tangent kernel regression derived at the random initialization. As a result of the deviation, we prove the at-most sublinear convergence for QNNs with Pauli measurements, which is beyond the explanatory power of any kernel regression dynamics. We then present the actual dynamics of QNNs in the limit of over-parameterization. The new dynamics capture the change of convergence rate during training and implies that the range of measurements is crucial to the fast QNN convergence.
- A Convergence Theory for Over-parameterized Variational Quantum Eigensolvers
-
QIP 2023.Links: arXiv:2205.12481Abstract:
The Variational Quantum Eigensolver (VQE) is a promising candidate for quantum applications on near-term Noisy Intermediate-Scale Quantum (NISQ) computers. Despite a lot of empirical studies and recent progress in theoretical understanding on VQE's optimization landscape, the convergence for optimizing VQE is far less understood. We provide the first rigorous analysis of the convergence of VQEs in the over-parameterization regime. By connecting the training dynamics with the Riemannian Gradient Flow on the unit-sphere, we establish a threshold on the sufficient number of parameters for efficient convergence, which depends polynomially on the system dimension and the spectral ratio, a property of the problem Hamiltonian, and could be resilient to gradient noise to some extent. We further illustrate that this over-parameterization threshold could be vastly reduced for specific VQE instances by establishing an ansatz-dependent threshold paralleling our main result. We showcase that our ansatz-dependent threshold could serve as a proxy of the trainability of different VQE ansatzes without performing empirical experiments, which hence leads to a principled way of evaluating ansatz design. Finally, we conclude with a comprehensive empirical study that supports our theoretical findings.
- A Formally Certified End-to-End Implementation of Shor's Factorization Algorithm
-
Links: ArXiv: 2204.07112Abstract:
Quantum computing technology may soon deliver revolutionary improvements in algorithmic performance, but these are only useful if computed answers are correct. While hardware-level decoherence errors have garnered significant attention, a less recognized obstacle to correctness is that of human programming errors – bugs. Techniques familiar to most programmers from the classical domain for avoiding, discovering, and diagnosing bugs do not easily transfer, at scale, to the quantum domain because of its unique characteristics. To address this problem, we have been working to adapt formal methods to quantum programming. With such methods, a programmer writes a mathematical specification alongside their program, and semi-automatically proves the program correct with respect to it. The proof's validity is automatically confirmed - certified by a “proof assistant.” Formal methods have successfully yielded high-assurance classical software artifacts, and the underlying technology has produced certified proofs of major mathematical theorems. As a demonstration of the feasibility of applying formal methods to quantum programming, we present the first formally certified end-to-end implementation of Shor's prime factorization algorithm, developed as part of a novel framework of applying the certified approach to general applications. By leveraging our framework, one can significantly reduce the effects of human errors and obtain high-assurance implementation of large-scale quantum applications in a principled way.
- Differentiable Analog Quantum Computing for Optimization and Control
-
Links: arXiv:2210.15812Abstract:
We formulate the first differentiable analog quantum computing framework with a specific parameterization design at the analog signal (pulse) level to better exploit near-term quantum devices via variational methods. We further propose a scalable approach to estimate the gradients of quantum dynamics using a forward pass with Monte Carlo sampling, which leads to a quantum stochastic gradient descent algorithm for scalable gradient-based training in our framework. Applying our framework to quantum optimization and control, we observe a significant advantage of differentiable analog quantum computing against SOTAs based on parameterized digital quantum circuits by orders of magnitude.
- Differentiable Quantum Programming with Unbounded Loops
-
Accepted by ACM Transactions on Software Engineering and Methodology, 2023.Links: arXiv: 2211.04507Abstract:
The emergence of variational quantum applications has led to the development of automatic differentiation techniques in quantum computing. Recently, Zhu et al. 2020 have formulated differentiable quantum programming with bounded loops, providing a framework for scalable gradient calculation by quantum means for training quantum variational applications. However, promising parameterized quantum applications, e.g., quantum walk and unitary implementation, cannot be trained in the existing framework due to the natural involvement of unbounded loops. To fill in the gap, we provide the first differentiable quantum programming framework with unbounded loops, including a newly designed differentiation rule, code transformation, and their correctness proof. Technically, we introduce a randomized estimator for derivatives to deal with the infinite sum in the differentiation of unbounded loops, whose applicability in classical and probabilistic programming is also discussed. We implement our framework with Python and Q#, and demonstrate a reasonable sample efficiency. Through extensive case studies, we showcase an exciting application of our framework in automatically identifying close-to-optimal parameters for several parameterized quantum applications.
- Quantum Variational Methods for Quantum Applications
-
Invited Paper at the Special Session of ICCAD 2021.Links:Abstract:
Quantum Variational Methods are promising near-term applications of quantum machines, not only because of their potential advantages in solving certain computational tasks and understanding quantum physics but also because of their feasibility on near-term quantum machines. However, many challenges remain in order to unleash the full potential of quantum variational methods, especially in the design of efficient training methods for each domain-specific quantum variational ansatzes. This paper proposes a theory-guided principle in order to tackle the training issue of quantum variational methods and highlights some successful examples.
- Verified Compilation of Quantum Oracles
-
Links: ArXiv: 2112.06700Abstract:
Quantum algorithms often apply classical operations, such as arithmetic or predicate checks, over a quantum superposition of classical data; these so-called oracles are often the largest components of a quantum program. To ease the construction of efficient, correct oracle functions, this paper presents vqo, a high-assurance framework implemented with the Coq proof assistant. The core of vqo is Oqasm, the oracle quantum assembly language. Oqasm operations move qubits between two different bases via the quantum Fourier transform, thus admitting important optimizations, but without inducing entanglement and the exponential blowup that comes with it. Oqasm’s design enabled us to prove correct vqo’s compilers—from a simple imperative language called Oqimp to Oqasm, and from Oqasm to sqir, a general-purpose quantum assembly language—and allowed us to efficiently test properties of Oqasm programs using the QuickChick property-based testing framework. We have used vqo to implement a variety of arithmetic and geometric operators that are building blocks for important oracles, including those used in Shor’s and Grover’s algorithms. We found that vqo’s QFT-based arithmetic oracles require fewer qubits, sometimes substantially fewer, than those constructed using “classical” gates; vqo’s versions of the latter were nevertheless on par with or better than (in terms of both qubit and gate counts) oracles produced by Quipper, a state-of-the-art but unverified quantum programming platform.
- Two-way Separations in Expressivity between Quantum Neural Networks and Feed-forward ReLU Networks
-
. Manuscript, 2021.Links:Abstract:
Quantum Neural Networks (QNNs) have been proposed as a variational method to realize a quantum advantage on near-term quantum computers. Despite the popularity of these models and some empirical evidence indicating their utility, there has yet to be a thorough analysis of their expressivity compared to classical parameterized models such as neural networks. In this work, we rigorously study separations in expressive power between QNNs and feedforward ReLU networks (ReNNs) with real-valued outputs, by investigating the model complexity (in terms of the input dimension and error) required to approximate various function classes. We discover advantages in expressivity in both directions: we demonstrate that constant and variable-depth ReNNs can be provably advantageous in expressing families of univariate and multivariate functions, while conversely QNNs have provable advantages over ReNNs of depth-2 in approximating certain univariate functions. We further conjecture that QNNs have advantages over ReNNs with depth>2, and carry out an empirical study to support this hypothesis. We also empirically verify the demonstrated provable separations in expressivity.
- EasyPQC: Verifying Post-Quantum Cryptography
-
In ACM Conference on Computer and Communication Security (CCS 2021).Links: iacr-eprint:2021/1253Abstract:
EasyCrypt is a formal verification tool used extensively for formalizing concrete security proofs of cryptographic constructions. However, the EasyCrypt formal logics consider only classical attackers, which means that post-quantum security proofs cannot be formalized and machine-checked with this tool. In this paper we prove that a natural extension of the EasyCrypt core logics permits capturing a wide class of post-quantum cryptography proofs, settling a question raised by (Unruh, POPL 2019). Leveraging our positive result, we implement EasyPQC, an extension of EasyCrypt for post-quantum security proofs, and use EasyPQC to verify post-quantum security of two classic constructions: Full Domain Hash and GPV08 identity-based encryption.
- Scalable Verification of Quantum Supremacy based on Circuit Obfuscation
-
Manuscript, 2021. GithubAbstract:
Exciting experimental progress has been made recently to demonstrate quantum supremacy in the examples of random circuit sampling and Boson sampling, whose verification procedure is how-ever exponentially expensive and hence extremely hard to scale to verify similar experiments of a slightly larger size. In this letter, we propose a practical and scalable scheme for verifiable quantum supremacy. Specifically, we define a type of quantum circuit obfuscators which significantly grows the size of the input circuit while keeping its original semantic. With such obfuscators, we can upgrade any circuit-based supremacy task to perform on larger size quantum machines while keeping the verification cost almost unchanged. The soundness of the upgraded protocol is supported by the hardness of the quantum counterpart of the minimum equivalent circuit problem. Inspired by the practical challenge in optimizing quantum circuits, we provide a construction of such obfuscators by roughly applying the reversed rewrites from existing quantum circuit optimizers in a random order. We have implemented a prototype of this construction and empirically verified its performance against all existing off-the-shelf tools. It is worth noting that our construction is highly extensible and can be easily adjusted for specific supremacy tasks and experimental platforms.
- Automating NISQ Application Design with Meta Quantum Circuits with Constraints (MQCC)
-
ACM Transaction on Quantum Computing vol. 4, issue 3, article no.16, pp 1-29. 2023. GithubAbstract:
Near-term intermediate-scale quantum (NISQ) computers are likely to have very restricted hardware resources, where precisely controllable qubits are expensive, error-prone, and scarce. Application designers for such computers must investigate the best balance of trade-offs among a large number of (potentially heterogeneous) factors specific to the targeted application and quantum hardware. To assist them, we propose Meta Quantum Circuits with Constraints (MQCC), a meta-programming framework for quantum programs. Designers express their application as a succinct collection of normal quantum circuits stitched together by a set of (manually or automatically) added meta-level choice variables, whose values are constrained according to a programmable set of quantitative optimization criteria. MQCC's compiler generates the appropriate constraints and solves them via an SMT solver, producing an optimized, runnable program. We demonstrate MQCC's expressiveness by easily encoding prior one-off NISQ application designs multi-programming (MP), crosstalk mitigation (CM) and building new ones, including a combined MP-CM, and an approach to writing approximate quantum Fourier transformation and quantum phase estimation that smoothly trades off accuracy and resource use.
- Algebraic Reasoning of Quantum Programs via Non-Idempotent Kleene Algebra
-
In the Proceedings of the 43rd ACM SIGPLAN PLDI 2022.Links: arXiv:2110.07018.Abstract:
We investigate the algebraic reasoning of quantum programs inspired by the success of classical program analysis based on Kleene algebra. One prominent example of such is the famous Kleene Algebra with Tests (KAT), which has furnished both theoretical insights and practical tools. The succinctness of algebraic reasoning would be especially desirable for scalable analysis of quantum programs, given the involvement of exponential-size matrices in most of the existing methods. A few key features of KAT including the idempotent law and the nice properties of classical tests, however, fail to hold in the context of quantum programs due to their unique quantum features, especially in branching. We propose the Non-idempotent Kleena Algebra (NKA) as a natural alternative, and identify complete and sound semantic models for NKA as well as their quantum interpretations. In light of applications of KAT, we demonstrate algebraic proofs in NKA of quantum compiler optimization and the normal form of quantum while-programs. Moreover, we extend NKA with Tests (i.e., NKAT), where tests model quantum predicates following effect algebra, and illustrate how to encode propositional quantum Hoare logic as NKAT theorems.
- Exponentially Many Local Minima in Quantum Neural Networks
-
Links: arXiv:2110.02479.Abstract:
Quantum Neural Networks (QNNs), or the so-called variational quantum circuits, are important quantum applications both because of their similar promises as classical neural networks and because of the feasibility of their implementation on near-term intermediate-size noisy quantum machines (NISQ). However, the training task of QNNs is challenging and much less understood. We conduct a quantitative investigation on the landscape of loss functions of QNNs and identify a class of simple yet extremely hard QNN instances for training. Specifically, we show for typical under-parameterized QNNs, there exists a dataset that induces a loss function with the number of spurious local minima depending exponentially on the number of parameters. Moreover, we show the optimality of our construction by providing an almost matching upper bound on such dependence. While local minima in classical neural networks are due to non-linear activations, in quantum neural networks local minima appear as a result of the quantum interference phenomenon. Finally, we empirically confirm that our constructions can indeed be hard instances in practice with typical gradient-based optimizers, which demonstrates the practical value of our findings.
- Sublinear Classical and Quantum Algorithms for General Matrix Games
-
Appeared at the 35th AAAI Conference on Artificial Intelligence (AAAI 2021).Links: arXiv:2012.06519.Abstract:
We investigate sublinear classical and quantum algorithms for matrix games, a fundamental problem in optimization and machine learning, with provable guarantees. Given a matrix
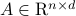 , sublinear algorithms for the matrix game
, sublinear algorithms for the matrix game 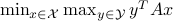 were previously known only for two special cases: (1)
were previously known only for two special cases: (1) 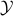 being the
being the 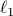 -norm unit ball, and (2)
-norm unit ball, and (2) 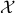 being either the
being either the 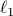 - or the
- or the 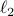 -norm unit ball. We give a sublinear classical algorithm that can interpolate smoothly between these two cases: for any fixed
-norm unit ball. We give a sublinear classical algorithm that can interpolate smoothly between these two cases: for any fixed ![qin (1,2]](eqs/622004514006138124-130.png) , we solve the matrix game where
, we solve the matrix game where 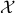 is a
is a 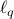 -norm unit ball within additive error
-norm unit ball within additive error  in time
in time 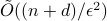 . We also provide a corresponding sublinear quantum algorithm that solves the same task in time
. We also provide a corresponding sublinear quantum algorithm that solves the same task in time 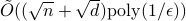 with a quadratic improvement in both
with a quadratic improvement in both 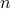 and
and 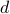 . Both our classical and quantum algorithms are optimal in the dimension parameters
. Both our classical and quantum algorithms are optimal in the dimension parameters 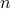 and
and 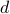 up to poly-logarithmic factors. Finally, we demonstrate sublinear classical and quantum algorithms for the approximate Caratheodory problem and the
up to poly-logarithmic factors. Finally, we demonstrate sublinear classical and quantum algorithms for the approximate Caratheodory problem and the 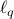 -margin support vector machines as applications.
-margin support vector machines as applications. - Constant-round Blind Classical Verification of Quantum Sampling
-
Eurocrypt 2022. Also available at arXiv:2012.04848.Links: arXiv:2012.04848.Abstract:
In a recent breakthrough, Mahadev constructed a classical verification of quantum computation (CVQC) protocol for a classical client to delegate decision problems in BQP to an untrusted quantum prover under computational assumptions. In this work, we explore further the feasibility of CVQC with the more general sampling problems in BQP and with the desirable blindness property. We contribute affirmative solutions to both as follows.
(1) Motivated by the sampling nature of many quantum applications (e.g., quantum algorithms for machine learning and quantum supremacy tasks), we initiate the study of CVQC for emph{quantum sampling problems} (denoted by SampBQP). Precisely, given an input
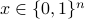 and a quantum circuit
and a quantum circuit 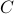 , the goal of a classical client is to learn a sample of output
, the goal of a classical client is to learn a sample of output 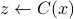 over
over 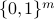 with the correct distribution up to a small error from an untrusted prover. We demonstrate its feasibility by constructing a four-message CVQC protocol for SampBQP based on the quantum Learning With Error assumption.
with the correct distribution up to a small error from an untrusted prover. We demonstrate its feasibility by constructing a four-message CVQC protocol for SampBQP based on the quantum Learning With Error assumption.(2) The blindness of CVQC protocols refers to a property of the protocol where the prover learns nothing, and hence is blind, about the client's input. It is a highly desirable property that has been intensively studied for the delegation of quantum computation. Somewhat surprisingly, we provide a simple yet powerful generic compiler that transforms any CVQC protocol to a blind one while preserving completeness and soundness errors.
Applying our compiler to (a parallel repetition of) Mahadev's protocol for BQP and our CVQC protocol for SampBQP yields the first constant-round blind CVQC protocol for BQP and SampBQP respectively, with negligible completeness and soundness errors.
- A Verified Optimizer for Quantum Circuits
-
Appeared as a distinguished paper at the 48th ACM SIGPLAN Symposium on Principles of Programming Languages (POPL 2021). GitHubLinks: arXiv:1912.02250.Abstract:
We present VOQC, the first fully verified compiler for quantum circuits, written using the Coq proof assistant. Quantum circuits are expressed as programs in a simple, low-level language called SQIR, which is deeply embedded in Coq. Optimizations and other transformations are expressed as Coq functions, which are proved correct with respect to a semantics of SQIR programs. SQIR uses a semantics of matrices of complex numbers, which is the standard for quantum computation, but treats matrices symbolically in order to reason about programs that use an arbitrary number of quantum bits. SQIR?s careful design and our provided automation make it easy to write and verify a broad range of optimizations in VOQC, and even allow us to verify correctness properties of interesting source SQIR programs.
- On the Theory and Practice of Invariant-based Verification of Quantum Programs
-
Manuscript, 2019.Links: preprint.Abstract:
We investigate program verification, a fundamental and challenging task in quantum programming, based on quantum Hoare logic and quantum invariants. Ying et al. (POPL’17) have developed a framework based on semidefinite programs (SDPs) for computing quantum invariants for partial correctness, which is however expensive to use due to its exponential scaling in terms of the number of qubits. In this paper, we develop two approaches that can effectively reuse the information generated from quantum invariants so as to avoid repetitive costs in solving exponentially large SDPs. Our first contribution is the formulation of the master Hoare triple that encodes the complete information of quantum programs inspired by the Choi-Jamiol{}kowski isomorphism. We demonstrate how to obtain the master Hoare triple by a single use of SDP, and once it is generated, how to obtain any other Hoare triple from the master one by a simple logic rule, and how master Hoare triples of sub-programs can be reused to simplify the computation of quantum invariants of the main program. Our second contribution is the introduction of approximate quantum invariants and a framework to reuse invariants of any given quantum program to efficiently analyze its nearby (e.g., noisy, erroneous) programs without using SDPs. Finally, we demonstrate the use of our techniques on realistic quantum programs, such as quantum Hamiltonian simulation and Repeat-Until-Success, with a huge numerical advantage over the previous SDP approach.
- On the Principles of Differentiable Quantum Programming Languages
-
Links: arXiv:2004.01122Abstract:
Variational Quantum Circuits (VQCs), or the so-called quantum neural-networks, are predicted to be one of the most important near-term quantum applications, not only because of their similar promises as classical neural-networks, but also because of their feasibility on near-term noisy intermediate-size quantum (NISQ) machines. The need for gradient information in the training procedure of VQC applications has stimulated the interest and development of auto-differentiation techniques on quantum circuits. We propose the first formalization of this technique, not only in the context of quantum circuits but also for imperative quantum programs (e.g., with controls), inspired by the success of differentiable programming languages in classical machine learning. In particular, we overcome a few unique difficulties caused by exotic quantum features (such as quantum no-cloning) and provide a rigorous formulation of differentiation applied to bounded-loop imperative quantum programs, its code-transformation rules, as well as a sound logic to reason about their correctness. Moreover, we have implemented our code transformation in OCaml and demonstrated the resource-efficiency of our scheme both analytically and empirically. We also conduct a case study of training a VQC instance with controls, which shows the advantage of our scheme over existing auto-differentiation on quantum circuits without controls.
- Quantum algorithm for estimating volumes of convex bodies
-
ACM Transaction on Quantum Computing, vol. 4, issue 3, article no.20, pp 1-60. Earlier appeared at QIP 2020 as a single-track talk.Links: arXiv: 1908.03903Abstract:
Estimating the volume of a convex body is a central problem in convex geometry and can be viewed as a continuous version of counting. We present a quantum algorithm that estimates the volume of an
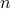 -dimensional convex body within multiplicative error
-dimensional convex body within multiplicative error  using
using 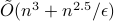 queries to a membership oracle and
queries to a membership oracle and 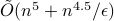 additional arithmetic operations. For comparison, the best known classical algorithm, due to Lovasz and Vempala, uses
additional arithmetic operations. For comparison, the best known classical algorithm, due to Lovasz and Vempala, uses  queries and
queries and 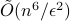 additional arithmetic operations. To the best of our knowledge, this is the first quantum speedup for volume estimation. Our algorithm is based on a refined framework for speeding up simulated annealing algorithms that might be of independent interest. This framework applies in the setting of "Chebyshev cooling’’, where the solution is expressed as a telescoping product of ratios, each having bounded variance. We develop several novel techniques when implementing our framework, including a theory of continuous-space quantum walks with rigorous bounds on discretization error.
additional arithmetic operations. To the best of our knowledge, this is the first quantum speedup for volume estimation. Our algorithm is based on a refined framework for speeding up simulated annealing algorithms that might be of independent interest. This framework applies in the setting of "Chebyshev cooling’’, where the solution is expressed as a telescoping product of ratios, each having bounded variance. We develop several novel techniques when implementing our framework, including a theory of continuous-space quantum walks with rigorous bounds on discretization error. - Quantum Wasserstein Generative Adversarial Networks
-
Links: arXiv:1911.00111Abstract:
The study of quantum generative models is well-motivated, not only because of its importance in quantum machine learning and quantum chemistry but also because of the perspective of its implementation on near-term quantum machines. Inspired by previous studies on the adversarial training of classical and quantum generative models, we propose the first design of quantum Wasserstein Generative Adversarial Networks (WGANs), which has been shown to improve the robustness and the scalability of the adversarial training of quantum generative models even on noisy quantum hardware. Specifically, we propose a definition of the Wasserstein semimetric between quantum data, which inherits a few key theoretical merits of its classical counterpart. We also demonstrate how to turn the quantum Wasserstein semimetric into a concrete design of quantum WGANs that can be efficiently implemented on quantum machines. Our numerical study, via classical simulation of quantum systems, shows the more robust and scalable numerical performance of our quantum WGANs over other quantum GAN proposals. As a surprising application, our quantum WGAN has been used to generate a 3-qubit quantum circuit of 50 gates that well approximates a 3-qubit 1-d Hamiltonian simulation circuit that requires over 10k gates using standard techniques.
- Verified Optimization in a Quantum Intermediate Representation
-
Manuscript, 2019. Extended abstract appeared at Quantum Physics and Logic (QPL) 2019.Links: arXiv:1904.06319Abstract:
We present sQIRe, a low-level language for quantum computing and verification. sQIRe uses a global register of quantum bits, allowing easy compilation to and from existing ‘quantum assembly’ languages and simplifying the verification process. We demonstrate the power of sQIRe as an intermediate representation of quantum programs by verifying a number of useful optimizations, and we demonstrate sQIRe's use as a tool for general verification by proving several quantum programs correct.
- Simulating large quantum circuits on a small quantum computer
-
Links: arXiv:1904.00102Abstract:
Limited quantum memory is one of the most important constraints for near-term quantum devices. Understanding whether a small quantum computer can simulate a larger quantum system, or execute an algorithm requiring more qubits than available, is both of theoretical and practical importance. In this Letter, we introduce cluster parameters
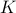 and
and 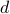 of a quantum circuit. The tensor network of such a circuit can be decomposed into clusters of size at most
of a quantum circuit. The tensor network of such a circuit can be decomposed into clusters of size at most 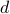 with at most
with at most 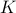 qubits of inter-cluster quantum communication. Our main result is a simulation scheme of any
qubits of inter-cluster quantum communication. Our main result is a simulation scheme of any 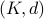 -clustered quantum circuit on a
-clustered quantum circuit on a 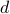 -qubit machine in time roughly
-qubit machine in time roughly 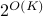 . An important application of our result is the simulation of clustered quantum systems — such as large molecules — that can be partitioned into multiple significantly smaller clusters with weak interactions among them. Another potential application is quantum optimization: we demonstrate numerically that variational quantum eigensolvers can still perform well when restricted to clustered circuits, thus making it feasible to study large quantum systems on small quantum devices.
. An important application of our result is the simulation of clustered quantum systems — such as large molecules — that can be partitioned into multiple significantly smaller clusters with weak interactions among them. Another potential application is quantum optimization: we demonstrate numerically that variational quantum eigensolvers can still perform well when restricted to clustered circuits, thus making it feasible to study large quantum systems on small quantum devices. - Sublinear quantum algorithms for training linear and kernel-based classifiers
-
Links: arXiv:1904.02276Abstract:
We investigate quantum algorithms for classification, a fundamental problem in machine learning, with provable guarantees. Given
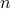
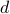 -dimensional data points, the state-of-the-art (and optimal) classical algorithm for training classifiers with constant margin et al. 2012 runs in
-dimensional data points, the state-of-the-art (and optimal) classical algorithm for training classifiers with constant margin et al. 2012 runs in 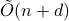 . We design sublinear quantum algorithms for the same task running in
. We design sublinear quantum algorithms for the same task running in 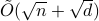 , a quadratic improvement in both
, a quadratic improvement in both 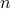 and
and 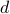 . Moreover, our algorithms use the standard quantization of the classical input and generate the same classical output, suggesting minimal overheads when used as subroutines for end-to-end applications. We also demonstrate a tight lower bound (up to poly-log factors) and discuss the possibility of implementation on near-term quantum machines. As a side result, we also give sublinear quantum algorithms for approximating the equilibria of
. Moreover, our algorithms use the standard quantization of the classical input and generate the same classical output, suggesting minimal overheads when used as subroutines for end-to-end applications. We also demonstrate a tight lower bound (up to poly-log factors) and discuss the possibility of implementation on near-term quantum machines. As a side result, we also give sublinear quantum algorithms for approximating the equilibria of 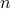 -dimensional matrix zero-sum games with optimal complexity
-dimensional matrix zero-sum games with optimal complexity 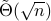 .
. - Quantitative Robustness Analysis of Quantum Programs
-
Appeared at the 46th ACM SIGPLAN POPL 2019.Links: arXiv:1811.03585Abstract:
Quantum computation is a topic of significant recent interest, with practical advances coming from both research and industry. A major challenge in quantum programming is dealing with errors (quantum noise) during execution. Because quantum resources (e.g., qubits) are scarce, classical error correction techniques applied at the level of the architecture are currently cost-prohibitive. But while this reality means that quantum programs are almost certain to have errors, there as yet exists no principled means to reason about erroneous behavior. This paper attempts to fill this gap by developing a semantics for erroneous quantum while-programs, as well as a logic for reasoning about them. This logic permits proving a property we have identified, called
 -robustness, which characterizes possible “distance” between an ideal program and an erroneous one. We have proved the logic sound, and showed its utility on several case studies, notably: (1) analyzing the robustness of noisy versions of the quantum Bernoulli factory (QBF) and quantum walk (QW); (2) demonstrating the (in)effectiveness of different error correction schemes on single-quibit errors; and (3) analyzing the robustness of a fault-tolerant version of QBF.
-robustness, which characterizes possible “distance” between an ideal program and an erroneous one. We have proved the logic sound, and showed its utility on several case studies, notably: (1) analyzing the robustness of noisy versions of the quantum Bernoulli factory (QBF) and quantum walk (QW); (2) demonstrating the (in)effectiveness of different error correction schemes on single-quibit errors; and (3) analyzing the robustness of a fault-tolerant version of QBF. - Quantum algorithms and lower bounds for convex optimization
-
Appeared at QIP 2019.Links: arXiv: 1809.01731Abstract:
While recent work suggests that quantum computers can speed up the solution of semidefinite programs, little is known about the quantum complexity of more general convex optimization. We present a quantum algorithm that can optimize a convex function over an
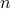 -dimensional convex body using
-dimensional convex body using  queries to oracles that evaluate the objective function and determine membership in the convex body. This represents a quadratic improvement over the best-known classical algorithm. We also study limitations on the power of quantum computers for general convex optimization, showing that it requires
queries to oracles that evaluate the objective function and determine membership in the convex body. This represents a quadratic improvement over the best-known classical algorithm. We also study limitations on the power of quantum computers for general convex optimization, showing that it requires  evaluation queries and
evaluation queries and 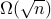 membership queries.
membership queries. - Quantum SDP Solvers: Large Speed-ups, Optimality, and Applications to Quantum Learning
-
. Appeared at QIP 2019. To appear at ICALP 2019.Links: arXiv: 1710.02581v2Abstract:
We give two new quantum algorithms for solving semidefinite programs (SDPs) providing quantum speed-ups. We consider SDP instances with
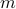 constraint matrices, each of dimension
constraint matrices, each of dimension 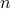 , rank at most
, rank at most  , and sparsity
, and sparsity  . The first algorithm assumes an input model where one is given access to an oracle to the entries of the matrices at unit cost. We show that it has run time
. The first algorithm assumes an input model where one is given access to an oracle to the entries of the matrices at unit cost. We show that it has run time 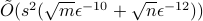 , with
, with  the error of the solution. This gives an optimal dependence in terms of
the error of the solution. This gives an optimal dependence in terms of 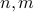 and a quadratic improvement over previous quantum algorithms (when
and a quadratic improvement over previous quantum algorithms (when 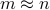 ). The second algorithms assumes a fully quantum input model in which the input matrices are given as quantum states. We show its run time is
). The second algorithms assumes a fully quantum input model in which the input matrices are given as quantum states. We show its run time is 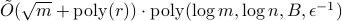 , with
, with 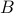 an upper bound on the trace-norm of all input matrices. In particular the complexity depends only poly-logarithmically in
an upper bound on the trace-norm of all input matrices. In particular the complexity depends only poly-logarithmically in 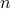 and polynomially in
and polynomially in  .
.We apply the second SDP solver to the problem of learning a good description of a quantum state with respect to a set of measurements: Given
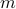 measurements and a supply of copies of an unknown state
measurements and a supply of copies of an unknown state 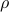 , we show we can find in time
, we show we can find in time 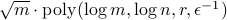 a description of the state as a quantum circuit preparing a density matrix which has the same expectation values as
a description of the state as a quantum circuit preparing a density matrix which has the same expectation values as 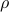 on the
on the 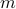 measurements, up to error
measurements, up to error  . The density matrix obtained is an approximation to the maximum entropy state consistent with the measurement data considered in Jaynes’ principle from statistical mechanics.
. The density matrix obtained is an approximation to the maximum entropy state consistent with the measurement data considered in Jaynes’ principle from statistical mechanics.As in previous work, we obtain our algorithm by ‘‘quantizing“ classical SDP solvers based on the matrix multiplicative weight update method. One of our main technical contributions is a quantum Gibbs state sampler for low-rank Hamiltonians, given quantum states encoding these Hamiltonians, with a poly-logarithmic dependence on its dimension, which is based on ideas developed in quantum principal component analysis. We also develop a ‘‘fast” quantum OR lemma with a quadratic improvement in gate complexity over the construction of Harrow et al. (SODA 2017). We believe both techniques might be of independent interest.
- Quantum query complexity of entropy estimation
-
. IEEE Transaction on Information Theory, Vol. 65, Issue 5, pages 2899 - 2921, May 2019. (link)Links: arXiv: 1710.06025Abstract:
Estimation of Shannon and R{'e}nyi entropies of unknown discrete distributions is a fundamental problem in statistical property testing and an active research topic in both theoretical computer science and information theory. Tight bounds of the number of samples to estimate these entropies have been established in the classical setting, while little is known about their quantum counterparts. In this paper, we give the first quantum algorithms for estimating
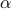 -R{'e}nyi entropies (Shannon entropy being 1-Renyi entropy). In particular, we demonstrate a quadratic quantum speedup for Shannon entropy estimation and a generic quantum speedup for
-R{'e}nyi entropies (Shannon entropy being 1-Renyi entropy). In particular, we demonstrate a quadratic quantum speedup for Shannon entropy estimation and a generic quantum speedup for 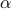 -R{'e}nyi entropy estimation for all
-R{'e}nyi entropy estimation for all 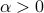 ,
including a tight bound for the collision-entropy (2-R{'e}nyi entropy) and also an analysis for the min-entropy case (i.e.,
,
including a tight bound for the collision-entropy (2-R{'e}nyi entropy) and also an analysis for the min-entropy case (i.e., 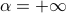 ). Moreover, we complement our quantum upper bounds with quantum lower bounds on
). Moreover, we complement our quantum upper bounds with quantum lower bounds on 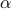 -R{'e}nyi entropy estimation for all
-R{'e}nyi entropy estimation for all 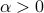 .
.Our approach is inspired by the pioneering work of Bravyi, Harrow, and Hassidim (BHH) on quantum algorithms for distributional property testing, however, with many new technical ingredients. For Shannon entropy estimation, we improve the performance of the BHH framework, especially its error dependence, using Montanaro's approach to estimating the expected output value of a quantum subroutine with bounded variance and giving a fine-tuned error analysis. For general
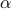 -R{'e}nyi entropy estimation, we further develop a procedure that recursively approximates
-R{'e}nyi entropy estimation, we further develop a procedure that recursively approximates 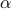 -R{'e}nyi entropy for a sequence of
-R{'e}nyi entropy for a sequence of 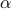 s, which is in spirit similar to the cooling schedules in simulated annealing.
For special cases like integer
s, which is in spirit similar to the cooling schedules in simulated annealing.
For special cases like integer 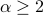 and
and 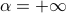 (i.e., the min-entropy case), we reduce the entropy estimation problem to the
(i.e., the min-entropy case), we reduce the entropy estimation problem to the 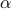 -distinctness and the
-distinctness and the 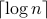 -distinctness problems respectively.
Finally, we exploit reductions as well as the polynomial method to obtain our lower bounds.
-distinctness problems respectively.
Finally, we exploit reductions as well as the polynomial method to obtain our lower bounds. - Raz-McKenzie simulation with the inner product gadget
-
. Manuscript, 2017Links: ECCC TR17-010Abstract:
In this note we show that the Raz-McKenzie simulation algorithm which lifts deterministic query lower bounds to deterministic communication lower bounds can be implemented for functions
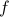 composed with the Inner Product gadget
composed with the Inner Product gadget 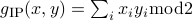 of logarithmic size. In other words, given a function
of logarithmic size. In other words, given a function 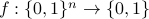 with deterministic query complexity
with deterministic query complexity 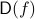 , we show that the deterministic communication complexity of the composed function
, we show that the deterministic communication complexity of the composed function 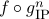 is
is 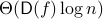 , where
, where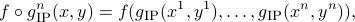
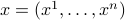 ,
, 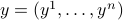 and each
and each 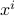 and
and 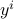 are
are  bit strings. In Raz-McKenzie and Goos-Pitassi-Watson, the simulation algorithm is implemented for functions composed with the Indexing gadget, where the size of the gadget is polynomial in the input length of the outer function
bit strings. In Raz-McKenzie and Goos-Pitassi-Watson, the simulation algorithm is implemented for functions composed with the Indexing gadget, where the size of the gadget is polynomial in the input length of the outer function 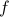 .
. - Computational Notions of Quantum Min-Entropy
-
. Appeared at the 7th International Conference on Quantum Cryptography (QCrypt 2017).Links: arXiv: 1704.07309Abstract:
Computational notions of entropy have many applications in cryptography and complexity theory. These notions measure how much (min-)entropy a source X has from the eyes of a computationally bounded party who may hold certain ?leakage information? B that is correlated with X. In this work, we initiate the study of computational entropy in the quantum setting, where X and/or B may become quantum states and the computationally bounded observer is modelled as a small quantum circuit. Specifically, we investigate to what extent the classical notions of computational entropy generalize to the quantum setting, and whether quantum analogues of classical theorems still hold. For example, we show:
There exist quantum states that are pseudorandom (i.e. they cannot be distinguished from the totally mixed state by polynomial-sized quantum circuits) but have actual entropy 0 (i.e. are pure states). In contrast, a classical distribution needs super-logarithmic entropy to be pseudorandom.
We extend the classical Leakage Chain Rule for pseudoentropy to the case where the leakage information B is quantum (while X remains classical). Specifically, if X has pseudoentropy at least k against quantum distinguishers (i.e. it is indistinguishable from some distribution of min-entropy at least k by polynomial-sized quantum distinguishers) and B consists of at most a logarithmic number l of qubits, then X conditioned on B has pseudoentropy at least k-l against quantum distinguishers.
We show that a general form of the classical Dense Model Theorem (interpreted as showing the equivalence between two definitions of pseudo-relative-min-entropy) does not extend to quantum states.
As an application, we construct the first quantum leakage-resilient stream-cipher in the quantum bounded storage model, assuming the existence of a quantum-secure PRG.
Along the way, we develop quantum analogues of a number of classical techniques (e.g. the Leakage Simulation Lemma, proven using a Non-uniform Min-Max Theorem or Boosting), and also identify classical techniques (namely, Gap Amplification) that do not hold in the quantum setting. Moreover, we introduce a variety of notions that combine quantum information and quantum complexity, which raise a number of directions for future work.
- General randomness amplification with non-signaling security
-
. Appeared at QIP 2017Links: preprintAbstract:
Highly unpredictable events appear to be abundant in life. However, when modeled rigorously, their existence in nature is far from evident. In fact, the world can be deterministic while at the same time the predictions of quantum mechanics are consistent with observations. Assuming that randomness does exist but only in a weak form, could highly random events be possible? This fundamental question was first raised by Colbeck and Renner (Nature Physics, 8:450–453, 2012). In this work, we answer this question positively, without the various restrictions assumed in the previous works. More precisely, our protocol uses quantum devices, a single weak randomness source quantified by a general notion of non-signaling min-entropy, tolerates a constant amount of device imperfection, and the security is against an all-powerful non-signaling adversary. Unlike the previous works proving non-signaling security, our result does not rely on any structural restrictions or independence assumptions. Thus it implies a stronger interpretation of the dichotomy statement articulated by Gallego et al. (Nature Communications, 4:2654, 2013): ‘‘either our world is fully deterministic or there exist in nature events that are fully random.’’
Note: This is a new work after our QIP 2014 paper, where the security proved is against a quantum, as opposed to non-signaling, adversary.
- Limitations of semidefinite programs for separable states and entangled games
-
. Appeared at QIP 2017. Communications in Mathematical Physics, Volume 366, Issue 2, pp 423--468, 2019.Links: arXiv:1612.09306Abstract:
We introduce a method for using reductions to construct integrality gaps for semidefinite programs (SDPs). These imply new limitations on the sum-of-squares (SoS) hierarchy in two settings where previously no
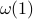 -round integrality gaps were known:
-round integrality gaps were known:The set of separable (i.e. unentangled) quantum states, or equivalently, the
 norm of a matrix.
norm of a matrix.The set of quantum correlations; i.e. conditional probability distributions achievable with local measurements on a shared entangled state.
Integrality gaps for the
 norm had previously been sought due
to its connection to Small-Set Expansion (SSE) and Unique Games (UG).
norm had previously been sought due
to its connection to Small-Set Expansion (SSE) and Unique Games (UG).In both cases no-go theorems were previously known based on computational assumptions such as the Exponential Time Hypothesis (ETH) which asserts that 3-SAT requires exponential time to solve. Our unconditional results achieve the same parameters as all of these previous results (for separable states) or as some of the previous results (for quantum correlations). In some cases we can make use of the framework of Lee-Raghavendra-Steurer (LRS) to establish integrality gaps for any SDP, not only the SoS hierarchy. Our hardness result on separable states also yields a dimension lower bound of approximate disentanglers, answering a question of Aaronson et al.
These results can be viewed as limitations on the monogamy principle, the PPT test, the ability of Tsirelson-type bounds to restrict quantum correlations, as well as the SDP hierarchies of Doherty-Parrilo-Spedalieri, Navascues-Pironio-Acin and Berta-Fawzi-Scholz. Indeed a wide range of past work in quantum information can be described as using an SDP on one of the above two problems and our results put broad limits on these lines of argument.
- Invariants of Quantum Programs: Characterizations and Generation
-
. Appeared at the 44th ACM SIGPLAN POPL 2017.Links: preprintAbstract:
Program invariant is a fundamental notion widely used in program verification and analysis. The aim of this paper is twofold: (i) find an appropriate definition of invariants for quantum programs; and (ii) develop an effective technique of invariant generation for verification and analysis of quantum programs. Interestingly, the notion of invariant can be defined for quantum programs in two different ways – additive invariants and multiplicative invariants – corresponding to two interpretations of implication in a continuous valued logic: the Lukasiewicz implication and the Godel implication. It is shown that both of them can be used to establish partial correctness of quantum programs. The problem of generating additive invariants of quantum programs is addressed by reducing it to an SDP (Semidefinite Programming) problem. This approach is applied with an SDP solver to generate invariants of two important quantum algorithms – quantum walk and quantum Metropolis sampling. Our examples show that the generated invariants can be used to verify correctness of these algorithms and are helpful in optimizing quantum Metropolis sampling. To our knowledge, this paper is the first attempt to define the notion of invariant and to develop a method of invariant generation for quantum programs.
- Tight SoS-degree bounds for approximate Nash equilibria
-
Links: preprintAbstract:
Nash equilibria always exist, but are widely conjectured to require time to find that is exponential in the number of strategies, even for two-player games. By contrast, a simple quasi-polynomial time algorithm, due to Lipton, Markakis and Mehta (LMM), can find approximate Nash equilibria, in which no player can improve their utility by more than
 by changing their strategy. The LMM algorithm can also be used to find an approximate Nash equilibrium with near-maximal total welfare. Matching hardness results for this optimization problem were found assuming the hardness of the planted-clique problem (by Hazan and Krauthgamer) and assuming the Exponential Time Hypothesis (by Braverman, Ko and Weinstein).
by changing their strategy. The LMM algorithm can also be used to find an approximate Nash equilibrium with near-maximal total welfare. Matching hardness results for this optimization problem were found assuming the hardness of the planted-clique problem (by Hazan and Krauthgamer) and assuming the Exponential Time Hypothesis (by Braverman, Ko and Weinstein).In this paper we consider the application of the sum-squares (SoS) algorithm from convex optimization to the problem of optimizing over Nash equilibria. We show the first unconditional lower bounds on the number of levels of SoS needed to achieve a constant factor approximation to this problem. While it may seem that Nash equilibria do not naturally lend themselves to convex optimization, we also describe a simple LP (linear programming) hierarchy that can find an approximate Nash equilibrium in time comparable to that of the LMM algorithm, although neither algorithm is obviously a generalization of the other. This LP can be viewed as arising from the SoS algorithm at
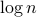 levels — matching our lower
bounds. The lower bounds involve a modification of the
Braverman-Ko-Weinstein embedding of CSPs into strategic games and
techniques from sum-of-squares proof systems. The upper bound
(i.e. analysis of the LP) uses information-theory techniques that
have been recently applied to other linear- and
semidefinite-programming hierarchies.
levels — matching our lower
bounds. The lower bounds involve a modification of the
Braverman-Ko-Weinstein embedding of CSPs into strategic games and
techniques from sum-of-squares proof systems. The upper bound
(i.e. analysis of the LP) uses information-theory techniques that
have been recently applied to other linear- and
semidefinite-programming hierarchies. - Sample-optimal tomography of quantum states
-
Links: arXiv:1508.01797Abstract:
It is a fundamental problem to decide how many copies of an unknown mixed quantum state are necessary and sufficient to determine the state. Previously, it was known only that estimating states to error
 in trace distance
required
in trace distance
required 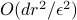 copies for a
copies for a 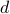 -dimensional density matrix of
rank
-dimensional density matrix of
rank  . Here, we give a theoretical measurement scheme (POVM) that requires
. Here, we give a theoretical measurement scheme (POVM) that requires
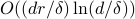 copies of
copies of 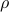 to error
to error  in
infidelity, and a matching lower bound up to logarithmic factors. This implies
in
infidelity, and a matching lower bound up to logarithmic factors. This implies
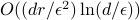 copies suffice to achieve error
copies suffice to achieve error
 in trace distance. For fixed
in trace distance. For fixed  , our measurement can be implemented
on a quantum computer in time polynomial in
, our measurement can be implemented
on a quantum computer in time polynomial in  .
. - An improved semidefinite programming hierarchy for testing entanglement
-
. Communications in Mathematical Physics, June 2017, Volume 352, Issue 3, pp 881--904.Links: arXiv: 1506.08834, journal versionAbstract:
We present a stronger version of the Doherty-Parrilo-Spedalieri (DPS) hierarchy of approximations for the set of separable states. Unlike DPS, our hierarchy converges exactly at a finite number of rounds for any fixed input dimension. This yields an algorithm for separability testing which is singly exponential in dimension and polylogarithmic in accuracy. Our analysis makes use of tools from algebraic geometry, but our algorithm is elementary and differs from DPS only by one simple additional collection of constraints.
- On the Limits of Communication with Non-local Resources
-
. Manuscript, 2015.Links: preprintAbstract:
We obtain optimal bounds for the problem of conveying classical messages by communication between a sender and receiver who can utilize non-local correlations obeying the Non-Signaling Principle. These include correlations arising from quantum entanglement, but also include ‘‘super-quantum’’ correlations (e.g. those that maximally violate the CHSH inequality). Our result simultaneously simplifies and generalizes the result of Nayak and Salzman (JACM vol.53, issue 1, pp. 184–206).
- Parallel repetition for entangled k-player games via fast quantum search
-
Links: ArXiv:1501.00033 • Conference ProceedingAbstract:
We present two parallel repetition theorems for the entangled value of multi-player, one-round free games (games where the inputs come from a product distribution). Our first theorem shows that for a
 -player free game
-player free game 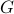 with entangled value
with entangled value  , the
, the 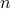 -fold repetition of
-fold repetition of 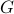 has entangled value
has entangled value 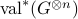 at most
at most 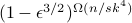 , where
, where  is the answer length of any player. In contrast, the best known parallel repetition theorem for the emph{classical} value of two-player free games is
is the answer length of any player. In contrast, the best known parallel repetition theorem for the emph{classical} value of two-player free games is 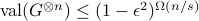 , due to Barak, et al. (RANDOM 2009). This suggests the possibility of a separation between the behavior of entangled and classical free games under parallel repetition.
Our second theorem handles the broader class of free games
, due to Barak, et al. (RANDOM 2009). This suggests the possibility of a separation between the behavior of entangled and classical free games under parallel repetition.
Our second theorem handles the broader class of free games 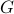 where the players can output (possibly entangled) quantum states. For such games, the repeated entangled value is upper bounded by
where the players can output (possibly entangled) quantum states. For such games, the repeated entangled value is upper bounded by  . We also show that the dependence of the exponent on
. We also show that the dependence of the exponent on 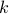 is necessary: we exhibit a
is necessary: we exhibit a 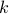 -player free game
-player free game 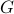 and
and 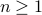 such that
such that 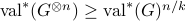 .
.Our analysis exploits the novel connection between communication protocols and quantum parallel repetition, first explored by Chailloux and Scarpa (ICALP 2014). We demonstrate that better communication protocols yield better parallel repetition theorems: in particular, our first theorem crucially uses a quantum search protocol by Aaronson and Ambainis, which gives a quadratic Grover speed-up for distributed search problems. Finally, our results apply to a broader class of games than were previously considered before; in particular, we obtain the first parallel repetition theorem for entangled games involving more than two players, and for games involving quantum outputs.
- Multi-Source Randomness Extractors Against Quantum Side Information, and their Applications
-
. Manuscript, 2014Links: ArXiv:1411.2315Abstract:
We study the problem of constructing multi-source extractors in the quantum setting, which extract almost uniform random bits against an adversary who collects quantum side information from several initially independent classical random sources. This is a natural generalization of the two much studied problems of seeded randomness extraction against quantum side information, and classical independent source extractors. With new challenges such as potential entanglement in the side information, it is not a prior clear under what conditions do quantum multi-source extractors exist; the only previous work in this setting is [KK12], where the classical inner-product two-source extractors of [CG88] and [DEOR04] are shown to be quantum secure in the restricted Independent Adversary (IA) Model and entangled Bounded Storage (BS) Model.
In this paper we propose a new model called General Entangled (GE) Adversary Model, which allows arbitrary entanglement in the side information and subsumes both the IA model and the BS model. We proceed to show how to construct GE-secure quantum multi-source extractors. To that end, we propose another model called One-sided Adversary (OA) Model, which is weaker than all the above models. Somewhat surprisingly, we establish an equivalence between strong OA-security and strong GE-security. As a result, all classical multi-source extractors can either directly work, or be modified to work in the GE model at the cost of one extra random source. Thus, our constructions essentially match the best known constructions of classical multi-source extractors. This answers several open questions in [KK12,DPVR12].
We also apply our techniques to two important problems in cryptography and distributed computing — privacy amplification and network extractor. Both problems deal with converting secret weak random sources into secret uniform random bits in a communicating environment, with the presence of a passive adversary who has unlimited computational power and can see every message transmitted. We show that as long as the sources have certain amounts of conditional min-entropy in our GE model (even with entangled quantum side information), we can design very efficient privacy amplification protocols and network extractors.
- Physical Randomness Extractors
-
. Plenary talk at the 17th Conference on Quantum Information Processing (QIP 2014).Abstract:
How to generate provably true randomness with minimal assumptions? This question is important not only for the efficiency and the security of information processing, but also for understanding how extremely unpredictable events are possible in Nature. All current solutions require special structures in the initial source of randomness, or a certain independence relation among two or more sources. Both types of assumptions are impossible to test and difficult to guarantee in practice. Here we show how this fundamental limit can be circumvented by extractors that base security on the validity of physical laws and extract randomness from untrusted quantum devices. In conjunction with the recent work of Miller and Shi (arXiv:1402:0489), our physical randomness extractor uses just a single and general weak source, produces an arbitrarily long and near-uniform output, with a close-to-optimal error, secure against all-powerful quantum adversaries, and tolerating a constant level of implementation imprecision. The source necessarily needs to be unpredictable to the devices, but otherwise can even be known to the adversary.
Our central technical contribution, the Equivalence Lemma, provides a general principle for proving composition security of untrusted-device protocols. It implies that unbounded randomness expansion can be achieved simply by cross-feeding any two expansion protocols. In particular, such an unbounded expansion can be made robust, which is known for the first time. Another significant implication is, it enables the secure randomness generation and key distribution using public randomness, such as that broadcast by NIST's Randomness Beacon. Our protocol also provides a method for refuting local hidden variable theories under a weak assumption on the available randomness for choosing the measurement settings.
- Limits of Quantum One-way Communication by Matrix Hypercontractive Inequality
-
. Manuscript, 2013.Links: preprintAbstract:
An important discovery in quantum information processing is that quantum one-way communication protocols can be exponentially more efficient than classical protocols. Those extraordinary quantum advantages were demonstrated through the Hidden Matching Problem and its variants, where the underlying basic task is to determine the parity of some
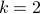 bits of an
bits of an  bit string. We prove that for larger values of
bit string. We prove that for larger values of  , the quantum complexities of those problems increase exponentially from
, the quantum complexities of those problems increase exponentially from  to
to 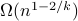 , which is almost tight and renders any super-polynomial quantum-classical gaps impossible. Our results also rule out a ‘‘quantum argument’’, in the sense of Kerenidis and de Wolf (Journal of Computer and System Sciences, 69(3)395–420, 2004), for proving an exponential lower bound on Locally Decodable Codes for more than
, which is almost tight and renders any super-polynomial quantum-classical gaps impossible. Our results also rule out a ‘‘quantum argument’’, in the sense of Kerenidis and de Wolf (Journal of Computer and System Sciences, 69(3)395–420, 2004), for proving an exponential lower bound on Locally Decodable Codes for more than 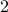 queries. Our proofs are new applications of the matrix Hypercontractive Inequality developed by Ben-Aroya, Regev, and de Wolf (FOCS 2008).
queries. Our proofs are new applications of the matrix Hypercontractive Inequality developed by Ben-Aroya, Regev, and de Wolf (FOCS 2008). - Epsilon-net method for optimizations over separable states
-
. Contributed talk at the 15th Workshop on Quantum Information Processing (QIP 2012). In the Proceedings of the 39th International Colloquium on Automata, Languages and Programming (ICALP 2012). Theoretical Computer Science, 2015 .Abstract:
We give algorithms for the optimization problem:
 , where
, where  is a Hermitian matrix, and the variable
is a Hermitian matrix, and the variable 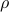 is a bipartite separable quantum state. This problem lies at the heart of several problems in quantum computation and information, such as the complexity of QMA(2). While the problem is NP-hard, our algorithms are better than brute force for several instances of interest. In particular, they give PSPACE upper bounds on promise problems admitting a QMA(2) protocol in which the verifier performs only logarithmic number of elementary gate on both proofs, as well as the promise problem of deciding if a bipartite local Hamiltonian has large or small ground energy. For
is a bipartite separable quantum state. This problem lies at the heart of several problems in quantum computation and information, such as the complexity of QMA(2). While the problem is NP-hard, our algorithms are better than brute force for several instances of interest. In particular, they give PSPACE upper bounds on promise problems admitting a QMA(2) protocol in which the verifier performs only logarithmic number of elementary gate on both proofs, as well as the promise problem of deciding if a bipartite local Hamiltonian has large or small ground energy. For 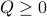 , our algorithm runs in time exponential in
, our algorithm runs in time exponential in 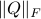 . While the existence of such an algorithm was first proved recently by Brandao, Christandl and Yard in Proceedings of the 43rd annual ACM Symposium on Theory of Computation , 343–352, 2011, our algorithm is conceptually simpler.
. While the existence of such an algorithm was first proved recently by Brandao, Christandl and Yard in Proceedings of the 43rd annual ACM Symposium on Theory of Computation , 343–352, 2011, our algorithm is conceptually simpler. - Parallel approximation of min-max problems with applications to classical and quantum zero-sum games
-
. Featured talk at the 15th Workshop on Quantum Information Processing (QIP 2012). In the Proceedings of the 27rd Annual IEEE Conference on Computational Complexity (CCC 2012). Computational Complexity, 22(2):385-428, 2013, the special issue of CCC 2012.Abstract:
This paper presents an efficient parallel algorithm for a new class of min-max problems based on the matrix multiplicative weights update method. Our algorithm can be used to find near-optimal strategies for competitive two-player classical or quantum games in which a referee exchanges any number of messages with one player followed by any number of additional messages with the other. This algorithm considerably extends the class of games which admit parallel solutions, demonstrating for the first time the existence of a parallel algorithm for a game in which one player reacts adaptively to the other. As a consequence, we prove that several competing-provers complexity classes collapse to PSPACE such as QRG, SQG and two new classes called DIP and DQIP. A special case of our result is a parallel approximation scheme for a new class of semidefinite programs whose feasible region consists of
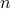 -tuples of semidefinite matrices that satisfy a ‘‘transcript-like’’ consistency condition. Applied to this special case, our algorithm yields a direct polynomial-space simulation of multi-message quantum interactive proofs resulting in a first-principles proof of QIP=PSPACE.
-tuples of semidefinite matrices that satisfy a ‘‘transcript-like’’ consistency condition. Applied to this special case, our algorithm yields a direct polynomial-space simulation of multi-message quantum interactive proofs resulting in a first-principles proof of QIP=PSPACE. - Parallelized Solution to Semidefinite Programmings in Quantum Complexity Theory
-
. Manuscript, 2010. Note: most of the techniques in this paper are applied and improved in the above paper. However, this paper contains more examples of the applications of such techniques.Links: arXiv:1009.2211Abstract:
In this paper we present an equilibrium value based framework for solving SDPs via the multiplicative weight update method which is different from the one in Kale's thesis [Kale07]. One of the main advantages of the new framework is that we can guarantee the convertibility from approximate to exact feasibility in a much more general class of SDPs than previous result. Another advantage is the design of the oracle which is necessary for applying the multiplicative weight update method is much simplified in the general case. This leads to an alternative and easier solutions to the SDPs used in the previous results QIP(2)
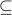 PSPACE [JainUW09] and QMAM=PSPACE [JainJUW09]. Furthermore, we provide a generic form of SDPs which can be solved in the similar way. By parallelizing every step in our solution, we are able to solve a class of SDPs in NC. Although our motivation is from quantum computing, our result will also apply to any SDP which satisfies our conditions directly.
PSPACE [JainUW09] and QMAM=PSPACE [JainJUW09]. Furthermore, we provide a generic form of SDPs which can be solved in the similar way. By parallelizing every step in our solution, we are able to solve a class of SDPs in NC. Although our motivation is from quantum computing, our result will also apply to any SDP which satisfies our conditions directly.In addition to the new framework for solving SDPs, we also provide a novel framework which improves the range of equilibrium value problems that can be solved via the multiplicative weight update method. Before this work we are only able to calculate the equilibrium value where one of the two convex sets needs to be the set of density operators. Our work demonstrates that in the case when one set is the set of density operators with further linear constraints, we are still able to approximate the equilibrium value to high precision via the multiplicative weight update method.
- Equilibrium Value Method for the proof of QIP=PSPACE
-
. Manuscript, 2010.Links: arXiv:1004.0264Abstract:
We provide an alternative proof of QIP=PSPACE to the recent breakthrough result [JainJUW09]. Unlike solving some semidefinite program corresponding to the definition of the complexity class, our method starts with one QIP-complete problem which computes the diamond norm between two admissible quantum channels. The key observation is that we can convert the computation of the diamond norm into the computation of some equilibrium value, which could be interesting for its own sake. The later problem, different from semidefinite programs, is generally more structured and easier to solve. The multiplicative weight update method is also used to solve the equilibrium value problem, however, in a relatively simpler way than the original proof [JainJUW09]. Furthermore, we provide a generalized form of equilibrium value problems which can be solved in the same way as well as comparisons to semidefinite programs.
- Non-Identity Check Remains QMA-Complete for Short Circuits
-
. Contributed talk at AQIS09 (Asian Conference on Quantum Information Science)Links: arXiv:0906.5416Abstract:
In the Non-Identity Check problem, we are given a quantum circuit as input, and are asked whether it is far away from the identity or not. It is well known that this problem is QMA-complete [JWB05]. In this note, it is shown that the Non-Identity Check problem remains QMA-complete for circuits of short depth. Specifically, we prove that for constant depth quantum circuit in which each gate is given to
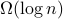 bits of precision, the Non-Identity Check problem is QMA-complete. It also follows that polylog depth circuit consisting of only gates from any universal gate set is QMA-complete.
bits of precision, the Non-Identity Check problem is QMA-complete. It also follows that polylog depth circuit consisting of only gates from any universal gate set is QMA-complete. - Exact Quantum Search by Parallel Unitary Discrimination Schemes
-
. Physical Review A, 78, 012303 (2008). Selected for the July 2008 issue of Virtual Journal of Quantum Information.Links: arXiv:0709.3627 • journalAbstract:
We study the unsorted database search problem with items
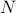 from the viewpoint of unitary discrimination. Instead of considering the famous
from the viewpoint of unitary discrimination. Instead of considering the famous 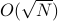 Grover's the bounded-error algorithm for the original problem, we seek for the results about the exact algorithms, i.e. the ones succeed with certainty. Under the standard oracle model
Grover's the bounded-error algorithm for the original problem, we seek for the results about the exact algorithms, i.e. the ones succeed with certainty. Under the standard oracle model 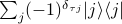 , we demonstrate a tight lower bound
, we demonstrate a tight lower bound 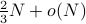 of the number of queries for any parallel scheme with unentangled input states. With the assistance of entanglement, we obtain a general lower bound
of the number of queries for any parallel scheme with unentangled input states. With the assistance of entanglement, we obtain a general lower bound 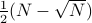 . We provide concrete examples to illustrate our results. In particular, we show that the case of
. We provide concrete examples to illustrate our results. In particular, we show that the case of 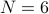 can be solved exactly with only two queries by using a bipartite entangled input state. Our results indicate that in the standard oracle model the complexity of exact quantum search with one unique solution can be strictly less than that of the calculation of OR function.
can be solved exactly with only two queries by using a bipartite entangled input state. Our results indicate that in the standard oracle model the complexity of exact quantum search with one unique solution can be strictly less than that of the calculation of OR function. - Verifier-based Algorithm for Unsorted Database Search Problem
-
. International Journal of Quantum Information, vol.5 no.4, pp 597 - 604 (2007)Links: journalAbstract:
Unsorted database search problem is an important science and engineering problem. We proposed quantum algorithm to solve the problem by dividing the database binarily and then use a probabilistic verifier algorithm to determine if the item is within one part of the divided database. We analyzed the computational complexity of this algorithm, and found that in general, the number of steps is proportional to that in the standard Grover algorithm. However in some cases, it is less than that of the Grover algorithm.
- Data Processing and software realization of wave-lengths of spectrum during CCD measurement (in Chinese)
-
Experimental Technology and Management, vol. 24, no. 4 p48-51 (2006)DOI: 10.3969/j.issn.1002-4956.2007.04.015