Books

Variations on a theorem by van der Waerden by Karen Johannson. Masters Thesis. HERE

Variations on a theorem by van der Waerden by Sohail Farhangi. Masters Thesis. Focus on the set of naturals the difference can come from. HERE

Van der waerden's theorem: Variants and “Applications” Very Rough Draft of a book on VDW material by Gasarch and Kruskal and Parrish HERE

Combinatorial Number Theory: Resuls of Hilbert, Schur, Folkman, and Hindman By Yudi Setyawan. Masters Degree HERE

Papers

Primitive recurive bounds on the VDW numbers by Saharon Shelah. HERE

On sets of integers containing no for elements in arithmetic progression by Endre Szemeredi. This has Szemeredi's Density theorem for k=4. HERE

Polynomial Extensions of VDW's and Sz's thm by Bergelson and Leibmancite{pvdw}. Has the original proof of Poly VDW thm. Using Ergodic Methods. HERE

Combinatorial Proofs of the Poly VDW thm and the Poly HJ theorem by Mark Walters This has the elementary proof of Poly VDW. HERE

A Partition Theorem by Shelah. Primitive Rec bounds on poly HJ so poly VDW. HERE

Set-Polynomials and Polynomial Extensions of the HJ thm by Bergelson and Leibman First proof of Poly-HJ. Uses Ergodic Theory. HERE

Two Combinatorial Theorems on Arithmetic Progressions by Wolfgang Schmidtcite{twocomb}. This gives some nice lower bounds on VDW numbers. Purely combinatorial. HERE

Monochromatic Equilateral Right Triangles in the Integer Grid By Graham and Solymosi. Gets a better upper bounds on W(3,c) as a corollary. HERE

A New Method to Construct Lower Bounds for VDW Numbers By Herwig, Heule, Lamblagen, an Maaren Purely Combinatorial. HERE

The van der Waerden Number 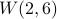is 1132 By Michal Kouril and Jerome Paul. HERE

Investigating Monte-Carlo Methods on the Weak Schur Problem by Eliahou, Fonlupt, Fromentin, Marion-Poty, Robilliard, Teytaud. They find n such that any 6-coloring of n has a mono x,y,z with x+y=z. HERE

On Sets of Integers Which Contain No Three Terms in Arithmetic Progession By Salem and Spencer. Purely Combinatorial. HERE

An improved construction of Progression-free sets by Michael Elkin. This paper improves Behrend result on large 3-free sts. Elementary. HERE

A note on Elkin's improvement of Behrend's Construction by Green and Wolfe. A shorter proof of Elkin's result HERE

On Sets of Integers Not Containing Long Arithmetic Progressiosn By Laba and Lacey Purely Combinatorial. HERE

Large 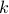-free sets based on Elkin's improvement of Behrends by Kevin O'Bryant. HERE

A Restricted Version of HJ Thm By Deuber, Promel, Rothschild. HERE

An Application of Lovasz Local Lemma —  A New Lower Bound for the van der Waerden Number by Soltan Szabo. HERE

A construction for partitions which avoid long arithmetic progressions by E. Berlekamp. HERE

Integer sets containing no arithmetic progressions by Szemeredi HERE

Integer sets containing no arithmetic progressions by Heath-Brown HERE

Triples in Arithmetic progression by Bourgain. HERE

Canonical Partition Theorems for parameter sets by H.J. Promel and B.Voight. They prove a very general canonical theorems. One of the corollaries is Can Hales-Jewitt. HERE

A lower bound for off-diagonal van der Waerden numbers by Yusheng Li and Jinlong Shu. HERE

Other Generalizations and Variants of VDW

Extremal binary matrices without constant 2-squares by Roland Batcher and Shalom Eliahou HERE In this paper they show that every 2-coloring of the 15 by 15 grid has a mono square.

On Monochromatic subsets of a rectangular grid By Maria Axenovich and Jacob Manske. They prove that any 2-coloring of VDW(8,2) by VDW(8,2) has a mono square. HERE

Searching for Monochromatic-Square-Free Ramsey Grid Colorings via SAT Solvers By Paul Walton and Wing Ning Li. This paper also has a 2-coloring of 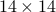without a mono square and shows you can't do 15. HERE

Independent Arithmetic progressions in clique-free graphs on the natural numbers by Gunderson, Rodl, Sidorenko. HERE

Ramsey's Theorem for 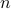-parameter sets by Graham and Rothschild. A very general from which follows VDW and Ramsey. HERE

Note on Combinatorial Analysis by Richard Rado. This contains both Rado's thm and Gallai-Witt thm. There is both a German version and an English version cite{radoenglish}. Purely Combinatorial. German Version English Version

Ein Kombinatorischer Satz der Elementgeometric (German) By Von Ernst Wittcite{witt}. Witt's article that contain Gallai-Witt thm. Purely Combinatorial but in German. HERE

An ergodic Szemeredi Theorem for commuting transformations By Furstenberg and Katznelson cite{densityGW}. This has a density version of the Gallai-Witt theorem. HERE

On Erdos-Rado Numbers By Lefmann and Rodl. They get better bounds on Can Ramsey Numbers for Graphs. HERE

An elementary proof of the canonizing version of Gallai-Witt's theorem by R{"o}dl and Pr{"o}mel. Purely Combinatorial. HERE My Notes on this paper

A Canonical Partition Theorem for Equivalence Relations on Z^n by Deuber, Graham, Promel, Voigt. Ergodic theorey or other hard techniques. HERE

Partition Theorems and Computability Theory by Joseph Mileti. HERE

Restricted Ramsey Configurations by Joel Spencer. Purely Combinatorial. HERE

VDW's thm on Homothetic Copies of {1,1s,1s+t} By Kim and Rho. HERE

Monochromatic Homothetic Copies of {1,1s,1s+t} HERE

APs in Sequences with Bounded Gaps by Tom Brown and Donavan Hare HERE

The 2-color relative linear VDW numbers by Kim and Rho. HERE

An Infinitary Polynomial VDW Theorem By McCutcheon. HERE

Rainbow Arithmetic Progression and Anti-Ramsey Results By Jungic, Licht, Mahdian, Nesteril, Radoicic. HERE

Difference sets without squares by I.Z. Ruzsa. HERE

On differences of sets of sequences of integers I by Sarkozy. HERE

Sets whose differences set is square-free by Julia Wolf. HERE

On sets of natural numbers whose difference set contains on squares By Pintz, Steiger, Szemeredi. HERE

On differences of sequences of integers III by Sarkozy HERE

Szemeredi's Theorem

Tau's exposition of Szemeredi's theorem by Tau. HERE

Notes on Sz's Reg Lemma by Ernie Croot. Good exposition! HERE

A New Proof of Sz's Thm for AP's of Length 4 By Gowers. HERE

Roth's Thm on AP's by Roth. Roth's original paper HERE NOTE by Iosevich

Sz Reg Lemma and its applications in Graph Theory By Komlos and Simonovitis. HERE

Ergodic behaviour of diagonal measures and a theorem of {S}zemer{'e}di on arithmetic progressions by Hillel Furstenberg. HERE

The Ergodic Theoretic Proof of Sz Thm By Furstenberg, Katznelson, Ornstein. HERE

A New Proof of Sz Thm By Gowers. HERE

An alternate proof of Szemeredi's cube lemma using extremal hypergraphs By Gunderson and Rodl. HERE