


Next: About this document ...
MATHNOTES
This is a collection of writeups of
theorems and other things, in math, I find interesting and felt
inspired to type in my notes for.
NONE of these results are mine.
- Ramsey Theory
- Ramsey's theorem for graphs
ramsey.PDF.
- Three proofs of the Hypergraph Ramsey Theorem (in progress)
higherramsey.PDF.
- An Application of Ramsey's Theorem to Proving Programs Terminate
(An exposition, a rough draft)
RAMSEYPL.PDF.
- An Exposition of Roth's Theorem which
states that `big' sets of integers must contain
arithmetic progressions of size 3.
Formally
![$(\forall \lambda>0)(\exists n_0\in N)(\forall n\ge n_0)(\forall A\subseteq [n])[\vert A\vert\ge
\lambda n \rightarrow \hbox{$A$ has a 3-AP}].$](img1.png) We present a combinatorial proof that is essentially due to Szemeredi.
SZ.PDF.
We present a combinatorial proof that is essentially due to Szemeredi.
SZ.PDF.
- (This is not a repeat of the last item.)
An Exposition of Roth's Theorem which
states that `big' sets of integers must contain
arithmetic progressions of size 3.
Formally
![$(\forall \lambda>0)(\exists n_0\in N)(\forall n\ge n_0)(\forall A\subseteq [n])[\vert A\vert\ge
\lambda n \rightarrow \hbox{$A$ has a 3-AP}].$](img1.png) We present Roth's proof which uses continous math.
ROTH.PDF.
We present Roth's proof which uses continous math.
ROTH.PDF.
- An Application of Ramsey Theory to Communication Complexity
PUDLAK.PDF.
This is a writeup of part of Pudlak's paper
An application of Hindman's Theorem to a problem
on Communication Complexity
- Van Der Waerden's Theorem- the k=3 Case.
For all c there exists W(c)} such that,
if you were to c-color {1,...,W(c),
then there would exist a sequence of three numbers,
in arithmetic progression, that are the same color!
We prove this in detail in
VDW3.PDF.
More generally still, for all c and for all k there exists W(c,k) such that,
if you were to c-color {1,...,W(c,k)},
then there would exist a sequence of k numbers,
in arithmetic progression, that are the same color!
- Equations and Infinite Colorings
An Exposition by Stephen Fenner and William Gasarch
Consider the following statement which we denote
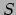 :
For every
:
For every 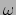 -coloring of
-coloring of 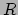 there exists
there exists
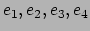 that are all the same color
such that
that are all the same color
such that
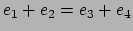 .
Is
.
Is 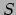 true or false? This exposition shows that
true or false? This exposition shows that
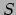 is true iff
is true iff 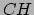 is false.
Hence
is false.
Hence 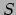 is true iff
is true iff 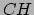 is false.
Hence
is false.
Hence 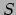 is ind of ZFC.
RADOZFC.PDF.
is ind of ZFC.
RADOZFC.PDF.
- Bounds on the Large Ramsey Numbers
An Expostion by Bill Gasarch
We show that
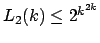 LARGERAMSEYTOOLONG.PDF.
A better bound is here:
LARGERAMSEY.PDF
LARGERAMSEYTOOLONG.PDF.
A better bound is here:
LARGERAMSEY.PDF
- Eucliean Ramsey Theory
ERAMSEY.PDF
- Ergodic proof of VDW's theorem
ERGODIC.PDF
Also good to have this cheat sheet while reading it:
HANDOUT.PDF
- The Infinite Ramsey Theorem
RAMSEYI.PDF
- Ramsey's original application of Ramsey's theorem
RAMSEYORIG.PDF
- Ramsey Theory for Open Sets
What if we color all infinite subsets of
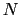 ¿:wq
OPENRAMSEY.PDF
¿:wq
OPENRAMSEY.PDF
- Logic
- It is well known that the Kolm function is not computable.
The usual proof does not reduce to HALT.
Hence it is plausible that the Kolm function is of intermediary
complexity. Its not. Oh well. In this proof we give the (well known to some)
proof that Kolm is equivalent to HALT.
EASYKOLM.PDF.
- An Exposition of the Main Theorem in
Enumerations of the Kolmogorov Function
Authors of paper:
Beigel, Buhrman, Fejer, Fortnow Grabowski, Longpre, Muchnik, Stephan, Torenvliet.
Let
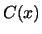 be the shortest description of
be the shortest description of 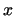 .
It is known that
.
It is known that  is undecidable (the proof of this is also
included). But what if we just want to, given
is undecidable (the proof of this is also
included). But what if we just want to, given 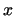 , enumerate
, enumerate 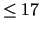 possibilities,
one of which is
possibilities,
one of which is 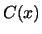 . This manuscript shows that this cannot be done.
KOLM.PDF.
. This manuscript shows that this cannot be done.
KOLM.PDF.
- Duplicator Spoiler Games
EF.PDF
- A statement in Second order True in (
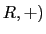 false in
false in 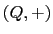 .
SECONDORDER.PDF
.
SECONDORDER.PDF
- Showing that a Propositional Logic is Incomplete.
PROP.PDF
- Complexity Theory
- Primality in P
For the original paper see
PRIMES.
For a write up that is suitable for undergrads
(but leaves out some of the proofs)
see
PRIMESHANDOUT.PDF.
(NOTE- This is more of an algorithms result.)
- Hardness vs Randomness.
Under certain Hardness assumptions you can derandomize a computation.
This is a writeup of the first result, due to Nisan-Wigderson, in that area.
HARDRAND.PDF.
Cheat sheet:
SHORTNW.PDF.
- If L is any set then SUBSEQ(L) is Regular
SUBSEQ.PDF
- Non-Ramsey Combinatorics
- Sum-Product Theorems
An Expostion by Bill Gasarch
We present proofs of the following two theorems:
- If
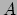 is a set of
is a set of 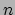 reals then either
reals then either 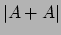 or
or 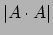 is
is
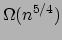 .
.
- If
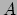 is a set of
is a set of 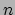 reals then either
reals then either 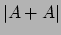 or
or 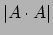 is
is
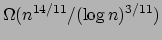 .
.
SUMPRODUCT.PDF.
- Fractional Graph Theory
We just define the fractional chromatic number of a graph.
FRACTIONAL.PDF.
- Monotone Sequence Game
MONOGAME.PDF.
- TicTacToe Plus
The Maker-breaker version of k-in-a-row on an nxn board.
TTTSURPLUS.PDF.
- The Weak Prime Number Theorem
WEAKPNT.PDF.
- Polynomials with Minimal Deviance- Chebyshev Polynomials
CHEBY.PDF.



Next: About this document ...
William Gasarch
2012-05-06
![$(\forall \lambda>0)(\exists n_0\in N)(\forall n\ge n_0)(\forall A\subseteq [n])[\vert A\vert\ge
\lambda n \rightarrow \hbox{$A$ has a 3-AP}].$](img1.png) We present a combinatorial proof that is essentially due to Szemeredi.
SZ.PDF.
We present a combinatorial proof that is essentially due to Szemeredi.
SZ.PDF.
![$(\forall \lambda>0)(\exists n_0\in N)(\forall n\ge n_0)(\forall A\subseteq [n])[\vert A\vert\ge
\lambda n \rightarrow \hbox{$A$ has a 3-AP}].$](img1.png) We present Roth's proof which uses continous math.
ROTH.PDF.
We present Roth's proof which uses continous math.
ROTH.PDF.
 :
For every
:
For every 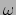 -coloring of
-coloring of 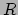 there exists
there exists
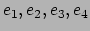 that are all the same color
such that
that are all the same color
such that
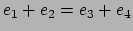 .
Is
.
Is 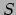 true or false? This exposition shows that
true or false? This exposition shows that
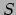 is true iff
is true iff 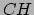 is false.
Hence
is false.
Hence 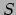 is true iff
is true iff 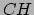 is false.
Hence
is false.
Hence 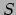 is ind of ZFC.
RADOZFC.PDF.
is ind of ZFC.
RADOZFC.PDF.
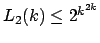 LARGERAMSEYTOOLONG.PDF.
A better bound is here:
LARGERAMSEY.PDF
LARGERAMSEYTOOLONG.PDF.
A better bound is here:
LARGERAMSEY.PDF
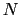 ¿:wq
OPENRAMSEY.PDF
¿:wq
OPENRAMSEY.PDF
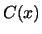 be the shortest description of
be the shortest description of 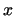 .
It is known that
.
It is known that 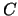 is undecidable (the proof of this is also
included). But what if we just want to, given
is undecidable (the proof of this is also
included). But what if we just want to, given 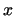 , enumerate
, enumerate 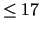 possibilities,
one of which is
possibilities,
one of which is 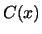 . This manuscript shows that this cannot be done.
KOLM.PDF.
. This manuscript shows that this cannot be done.
KOLM.PDF.
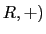 false in
false in 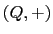 .
SECONDORDER.PDF
.
SECONDORDER.PDF
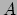 is a set of
is a set of 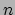 reals then either
reals then either 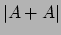 or
or 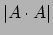 is
is
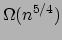 .
.
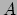 is a set of
is a set of 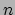 reals then either
reals then either 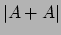 or
or 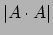 is
is
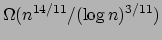 .
.