Van Der Waerden's Theorem}
Books
Variations on a theorem by van der Waerden by Karen Johannson. Masters Thesis. HERE
Variations on a theorem by van der Waerden by Sohail Farhangi. Masters Thesis. Focus on the set of naturals the difference can come from. HERE
Van der waerden's theorem: Variants and “Applications” Very Rough Draft of a book on VDW material by Gasarch and Kruskal and Parrish HERE
Combinatorial Number Theory: Resuls of Hilbert, Schur, Folkman, and Hindman By Yudi Setyawan. Masters Degree HERE
Papers
Primitive recurive bounds on the VDW numbers by Saharon Shelah. HERE
On sets of integers containing no for elements in arithmetic progression by Endre Szemeredi. This has Szemeredi's Density theorem for k=4. HERE
Polynomial Extensions of VDW's and Sz's thm by Bergelson and Leibmancite{pvdw}. Has the original proof of Poly VDW thm. Using Ergodic Methods. HERE
Combinatorial Proofs of the Poly VDW thm and the Poly HJ theorem by Mark Walters This has the elementary proof of Poly VDW. HERE
A Partition Theorem by Shelah. Primitive Rec bounds on poly HJ so poly VDW. HERE
Set-Polynomials and Polynomial Extensions of the HJ thm by Bergelson and Leibman First proof of Poly-HJ. Uses Ergodic Theory. HERE
Two Combinatorial Theorems on Arithmetic Progressions by Wolfgang Schmidtcite{twocomb}. This gives some nice lower bounds on VDW numbers. Purely combinatorial. HERE
Monochromatic Equilateral Right Triangles in the Integer Grid By Graham and Solymosi. Gets a better upper bounds on W(3,c) as a corollary. HERE
A New Method to Construct Lower Bounds for VDW Numbers By Herwig, Heule, Lamblagen, an Maaren Purely Combinatorial. HERE
The van der Waerden Number 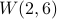 is 1132 By Michal Kouril and Jerome Paul.
HERE
is 1132 By Michal Kouril and Jerome Paul.
HERE
Investigating Monte-Carlo Methods on the Weak Schur Problem by Eliahou, Fonlupt, Fromentin, Marion-Poty, Robilliard, Teytaud. They find n such that any 6-coloring of n has a mono x,y,z with x+y=z. HERE
On Sets of Integers Which Contain No Three Terms in Arithmetic Progession By Salem and Spencer. Purely Combinatorial. HERE
An improved construction of Progression-free sets by Michael Elkin. This paper improves Behrend result on large 3-free sts. Elementary. HERE
A note on Elkin's improvement of Behrend's Construction by Green and Wolfe. A shorter proof of Elkin's result HERE
On Sets of Integers Not Containing Long Arithmetic Progressiosn By Laba and Lacey Purely Combinatorial. HERE
Large 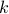 -free sets based on Elkin's improvement of Behrends by Kevin O'Bryant. HERE
-free sets based on Elkin's improvement of Behrends by Kevin O'Bryant. HERE
A Restricted Version of HJ Thm By Deuber, Promel, Rothschild. HERE
An Application of Lovasz Local Lemma — A New Lower Bound for the van der Waerden Number by Soltan Szabo. HERE
A construction for partitions which avoid long arithmetic progressions by E. Berlekamp. HERE
Integer sets containing no arithmetic progressions by Szemeredi HERE
Integer sets containing no arithmetic progressions by Heath-Brown HERE
Triples in Arithmetic progression by Bourgain. HERE
Canonical Partition Theorems for parameter sets by H.J. Promel and B.Voight. They prove a very general canonical theorems. One of the corollaries is Can Hales-Jewitt. HERE
A lower bound for off-diagonal van der Waerden numbers by Yusheng Li and Jinlong Shu. HERE
Other Generalizations and Variants of VDW
Extremal binary matrices without constant 2-squares by Roland Batcher and Shalom Eliahou HERE In this paper they show that every 2-coloring of the 15 by 15 grid has a mono square.
On Monochromatic subsets of a rectangular grid By Maria Axenovich and Jacob Manske. They prove that any 2-coloring of VDW(8,2) by VDW(8,2) has a mono square. HERE
Searching for Monochromatic-Square-Free Ramsey Grid Colorings via SAT Solvers By Paul Walton and Wing Ning Li. This paper also has a 2-coloring of 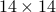 without a mono square and shows you can't do 15. HERE
without a mono square and shows you can't do 15. HERE
Independent Arithmetic progressions in clique-free graphs on the natural numbers by Gunderson, Rodl, Sidorenko. HERE
Ramsey's Theorem for 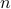 -parameter sets by Graham and Rothschild.
A very general from which follows VDW and Ramsey.
HERE
-parameter sets by Graham and Rothschild.
A very general from which follows VDW and Ramsey.
HERE
Note on Combinatorial Analysis by Richard Rado. This contains both Rado's thm and Gallai-Witt thm. There is both a German version and an English version cite{radoenglish}. Purely Combinatorial. German Version English Version
Ein Kombinatorischer Satz der Elementgeometric (German) By Von Ernst Wittcite{witt}. Witt's article that contain Gallai-Witt thm. Purely Combinatorial but in German. HERE
An ergodic Szemeredi Theorem for commuting transformations By Furstenberg and Katznelson cite{densityGW}. This has a density version of the Gallai-Witt theorem. HERE
On Erdos-Rado Numbers By Lefmann and Rodl. They get better bounds on Can Ramsey Numbers for Graphs. HERE
An elementary proof of the canonizing version of Gallai-Witt's theorem by R{"o}dl and Pr{"o}mel. Purely Combinatorial. HERE My Notes on this paper
A Canonical Partition Theorem for Equivalence Relations on Z^n by Deuber, Graham, Promel, Voigt. Ergodic theorey or other hard techniques. HERE
Partition Theorems and Computability Theory by Joseph Mileti. HERE
Restricted Ramsey Configurations by Joel Spencer. Purely Combinatorial. HERE
VDW's thm on Homothetic Copies of {1,1s,1s+t} By Kim and Rho. HERE
Monochromatic Homothetic Copies of {1,1s,1s+t} HERE
APs in Sequences with Bounded Gaps by Tom Brown and Donavan Hare HERE
The 2-color relative linear VDW numbers by Kim and Rho. HERE
An Infinitary Polynomial VDW Theorem By McCutcheon. HERE
Rainbow Arithmetic Progression and Anti-Ramsey Results By Jungic, Licht, Mahdian, Nesteril, Radoicic. HERE
Difference sets without squares by I.Z. Ruzsa. HERE
On differences of sets of sequences of integers I by Sarkozy. HERE
Sets whose differences set is square-free by Julia Wolf. HERE
On sets of natural numbers whose difference set contains on squares By Pintz, Steiger, Szemeredi. HERE
On differences of sequences of integers III by Sarkozy HERE
Szemeredi's Theorem
Tau's exposition of Szemeredi's theorem by Tau. HERE
Notes on Sz's Reg Lemma by Ernie Croot. Good exposition! HERE
A New Proof of Sz's Thm for AP's of Length 4 By Gowers. HERE
Roth's Thm on AP's by Roth. Roth's original paper HERE NOTE by Iosevich
Sz Reg Lemma and its applications in Graph Theory By Komlos and Simonovitis. HERE
Ergodic behaviour of diagonal measures and a theorem of {S}zemer{'e}di on arithmetic progressions by Hillel Furstenberg. HERE
The Ergodic Theoretic Proof of Sz Thm By Furstenberg, Katznelson, Ornstein. HERE
A New Proof of Sz Thm By Gowers. HERE
An alternate proof of Szemeredi's cube lemma using extremal hypergraphs By Gunderson and Rodl. HERE