24 Cache Optimizations II

 

The objectives of this module are to discuss the various factors that contribute to the average memory access time in a hierarchical memory system and discuss some of the techniques that can be adopted to improve the same.

 

Memory Access Time: In order to look at the performance of cache memories, we need to look at the average memory access time and the factors that will affect it. The average memory access time (AMAT) is defined as

 

AMAT = htc + (1 – h) (tm + tc), where tc in the second term is normally ignored.

 

h : hit ratio of the cache

tc : cache access time

 

1 – h : miss ratio of the cache

tm : main memory access time

 

AMAT can be written as hit time + (miss rate x miss penalty). Reducing any of these factors reduces AMAT. You can easily observe that as the hit ratio of the cache nears 1 (that is 100%), all the references are to the cache and the memory access time is governed only by the cache system. Only the cache performance matters then. On the other hand, if we miss in the cache, the miss penalty, which is the main memory access time also matters. So, all the three factors contribute to AMAT and optimizations can be carried out to reduce one or more of these parameters.

 

There are different methods that can be used to reduce the AMAT. There are about eighteen different cache optimizations that are organized into 4 categories as follows:

 

Ø    Reducing the miss penalty:

 

§    Multilevel caches, critical word first, giving priority to read misses over write misses, merging write buffer entries, and victim caches

 

Ø   Reducing the miss rate

 

§    Larger block size, larger cache size, higher associativity, way prediction and pseudo associativity, and compiler optimizations

 

Ø   Reducing the miss penalty or miss rate via parallelism

 

§    Non-blocking caches, Multi banked caches, hardware & compiler prefetching

 

§    Small and simple caches, avoiding address translation, pipelined cache access, and trace caches

 

The previous module discussed some optimizations that are done to reduce the miss penalty. We shall look at some more optimizations in this module. In this module, we shall discuss the techniques that can be used to reduce the miss rate. Five optimizations that can be used to address the problem of improving miss rate are:

• Larger block size
• Larger cache size
• Higher associativity
• Way prediction and pseudo associativity,  and
• Compiler optimizations.

We shall examine each of these in detail.

 

Different types of misses: Before we look at optimizations for reducing the miss rate, we shall look at the ‗3C‘ model and discuss the various types of misses. We know that miss rate is simply the fraction of cache accesses that result in a miss—that is, the number of accesses that miss in the cache divided by the number of accesses. In order to gain better insight into the causes of miss rates, the three C model sorts all misses into three simple categories:

• Compulsory – The very first access to a block cannot be in the cache, so the block must be brought into the cache. Compulsory misses are those that occur even if you had an infinite cache. They are also called cold start misses or first reference misses.
• Capacity – Because of the limited size of the cache, if the cache cannot contain all the blocks needed during execution of a program, capacity misses, apart from compulsory misses, will occur because of blocks being discarded and later retrieved.
• Conflict – If the block placement strategy is not fully associative, conflict misses (in addition to compulsory and capacity misses) will occur because a block may be discarded and later retrieved if conflicting blocks map to its set. They are also called collision misses or interference misses.

 

Figures 28.1 and 28.2 give the various miss rates for different cache sizes. Reducing any of these misses should reduce the miss rate. However, some of them can be contradictory. Reducing one may increase the other. We will also discuss about a fourth miss, called the coherence miss in multiprocessor systems later on.

 

 

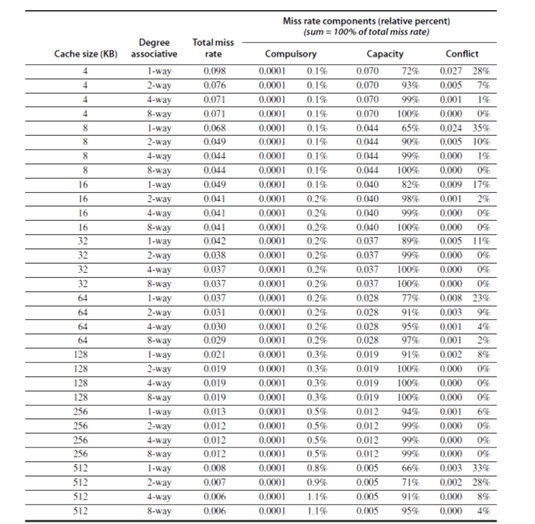
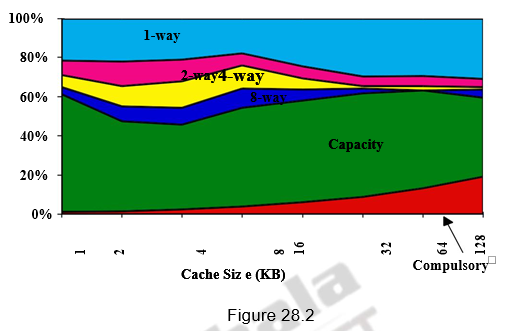
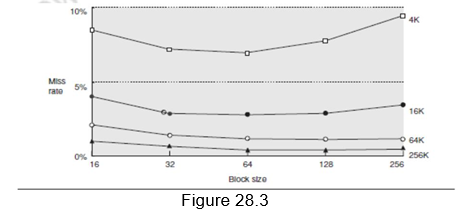
Larger block size: The simplest and obvious way to reduce the miss rate is to increase the block size. By increasing the block size, we are trying to exploit the spatial locality of reference in a better manner, and hence the reduction in miss rates. Larger block sizes will also reduce compulsory misses. At the same time, larger blocks increase the miss penalty. Since they reduce the number of blocks in the cache, larger blocks may increase conflict misses and even capacity misses if the cache is small. Figure 28.3 shows how the miss rate varies with block size for different cache sizes. It can be seen that beyond a point, increasing the block size increases the miss rate. Clearly, there is little reason to increase the block size to such a size that it increases the miss rate. There is also no benefit to reducing miss rate if it increases the average memory access time. The increase in miss penalty may outweigh the decrease in miss rate.

 

 

Larger cache size: The next optimization that we consider for reducing the miss rates is increasing the cache size itself. This is again an obvious solution. Increasing the size of the cache will reduce the capacity misses, given the same line size, since more number of blocks can be accommodated. However, the drawback is that the hit time increases and the power and cost also increase. This technique is popular in off-chip caches. Always remember the fact that execution time is the only final measure we can believe. We will have to analyze whether the clock cycle time increases as a result of having a more complicated cache, and then take an appropriate decision.

 

Higher associativity: This is related to the mapping strategy adopted. Fully associative mapping has the best associativity and direct mapping, the worst. But, for all practical purposes, 8-way set associative mapping itself is as good as fully associative mapping. The flexibility offered by higher associativity reduces the conflict misses. The 2:1 cache rule needs to be recalled here. It states that the miss rate of a direct mapped cache of size N and the miss rate of 2-way set associative cache of size N/2 are the same. Such is the importance of associativity. However, increasing the associativity increases the complexity of the cache. The hit time increases.

 

Way prediction and pseudo associativity: This is another approach that reduces conflict misses and also maintains the hit speed of direct-mapped caches. In this case, extra bits are kept in the cache, called block predictor bits, to predict the way, or block within the set of the next cache access. The bits select which of the blocks to try on the next cache access. If the predictor is correct, the cache access latency is the fast hit time. If not, it tries the other block, changes the way predictor, and has a latency of one extra clock cycle. This prediction means the multiplexor is set early to select the desired block, and only a single tag comparison is performed in that clock cycle in parallel with reading the cache data. A miss, of course, results in checking the other blocks for matches in the next clock cycle. The Pentium 4 uses way prediction. The Alpha 21264 uses way prediction in its instruction cache. In addition to improving performance, way prediction can reduce power for embedded applications, as power can be applied only to the half of the tags that are expected to be used.

 

A related approach is called pseudo-associative or column associative. Accesses proceed just as in the direct-mapped cache for a hit. On a miss, however, before going to the next lower level of the memory hierarchy, a second cache entry is checked to see if it matches there. A simple way is to invert the most significant bit of the index field to find the other block in the ―pseudo set.‖ Pseudo-associative caches then have one fast and one slow hit time—corresponding to a regular hit and a pseudo hit—in addition to the miss penalty. Figure 28.4 shows the relative times. One danger would be if many fast hit times of the direct-mapped cache became slow hit times in the pseudo-associative cache. The performance would then be degraded by this optimization. Hence, it is important to indicate for each set which block should be the fast hit and which should be the slow one. One way is simply to make the upper one fast and swap the contents of the blocks. Another danger is that the miss penalty may become slightly longer, adding the time to check another cache entry.

 

Compiler Optimizations: So far, we have discussed different hardware related techniques for reducing the miss rates. Now, we shall discuss some options that the compiler can provide to reduce the miss rates. The compiler can easily reorganize the code, without affecting the correctness of the program. The compiler can profile code, identify conflicting sequences and do the reorganization accordingly. Reordering the instructions reduced misses by 50% for a 2-KB direct-mapped instruction cache with 4-byte blocks, and by 75% in an 8-KB cache. Another code optimization aims for better efficiency from long cache blocks. Aligning basic blocks so that the entry point is at the beginning of a cache block decreases the chance of a cache miss for sequential code. This improves both spatial and temporal locality of reference.

 

Now, looking at the data, there are even fewer restrictions on location than code. These transformations try to improve the spatial and temporal locality of the data. The general rule that is always adopted is that, once a data has been brought to cache, use it to the fullest possibility and then put it back in memory. We should not keep shifting data between the cache and main memory. For example, exploit the spatial locality of reference when accessing arrays. If arrays are stored in a row major order (column major order), then also access them accordingly, so that they will be available within the same block. We should not blindly stride through arrays in the order the programmer happened to place the loop. The following techniques illustrate these concepts.

 

Loop Interchange: Some programs have nested loops that access data in memory in non-sequential order. Simply exchanging the nesting of the loops can make the code access the data in the order it is stored. Assuming the arrays do not fit in cache, this technique reduces misses by improving spatial locality. The reordering that is done maximizes the use of the data in a cache block before it is discarded.

 

/* Before */

 

for (j = 0; j < 100; j = j+1)

 

for (i = 0; i < 5000; i = i+1)

 

x[i][j] = 2 * x[i][j];

 

/* After */

 

for (i = 0; i < 5000; i = i+1)

 

for (j = 0; j < 100; j = j+1)

 

x[i][j] = 2 * x[i][j];

 

The original code would skip through memory in strides of 100 words, while the revised version accesses all the words in one cache block before going to the next block. This optimization improves cache performance without affecting the number of instructions executed.

 

Loop fusion: We can fuse two or more loops that operate on the same data, instead of doing the operations in two different loops. The goal again is to maximize the accesses to the data loaded into the cache before the data are replaced from the cache.

 

/* Before */

 

for (i = 0; i < N; i = i + 1)

 

for (j = 0; j < N; j = j + 1)

 

a [i][j] = 1/b [i][j] * c [i][j];

 

for (i = 0; i < N; i = i + 1)

 

for (j = 0; j < N; j = j + 1)

 

d [i][j] = a [i][j] + c [i][j];

 

/* After */

 

for (i = 0; i < N; i = i + 1)

 

for (j = 0; j < N; j = j + 1)

 

{a [i][j] = 1/b [i][j] * c [i][j];

 

d [i][j] = a [i][j] + c [i][j]; }

 

Note that instead of the two probable misses per access to a and c, we will have only one miss per access. This technique improves the temporal locality of reference.

 

Blocking: This optimization tries to reduce misses via improved temporal locality. Sometimes, we may have to access both rows and columns. Therefore, storing the arrays row by row (row major order) or column by column (column major order) does not solve the problem because both rows and columns are used in every iteration of the loop. Therefore, the previous techniques will not be helpful. Instead of operating on entire rows or columns of an array, blocked algorithms operate on submatrices or

 

blocks. The goal is to maximize accesses to the data loaded into the cache before the data are replaced. The code example below, which performs matrix multiplication, helps explain the optimization:

 

/* Before */

 

for (i = 0; i < N; i = i+1)

 

for (j = 0; j < N; j = j+1)

 

{r = 0;

 

for (k = 0; k < N; k = k + 1)

 

r = r + y[i][k]*z[k][j];

 

x[i][j] = r;

 

};

 

The two inner loops read all N by N elements of z, read the same N elements in a row of y repeatedly, and write one row of N elements of x. Figure 28.5 shows a snapshot of the accesses to the three arrays. A dark shade indicates a recent access, a light shade indicates an older access, and white means not yet accessed.

 

 

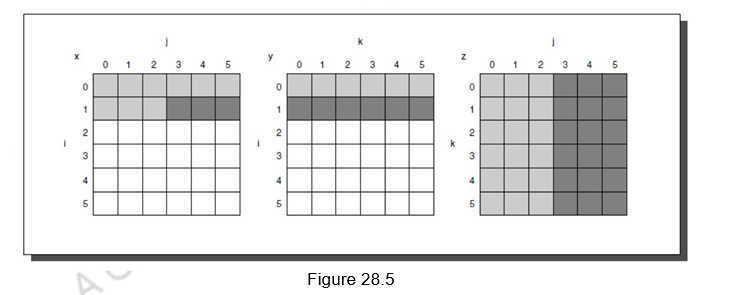
The number of capacity misses clearly depends on N and the size of the cache. If it can hold all three N by N matrices, then we don‘t have any problems, provided there are no cache conflicts. If the cache can hold one N by N matrix and one row of N, then at least the i-th row of y and the array z may stay in the cache. If we cannot accommodate even that in cache, then, misses may occur for both x and z. In the worst case, there would be 2N3 + N2 memory words accessed for N3 operations.

 

To ensure that the elements being accessed can fit in the cache, the original code is changed to compute on a submatrix of size B by B. Two inner loops now compute in steps of size B rather than the full length of x and z. B is called the blocking factor. (Assume x is initialized to zero.)

 

/* After */

 

for (jj = 0; jj < N; jj = jj+B)

 

for (kk = 0; kk < N; kk = kk+B)

 

for (i = 0; i < N; i = i+1)

 

for (j = jj; j < min(jj+B,N); j = j+1)

 

{r = 0;

 

for (k = kk; k < min(kk+B,N); k = k + 1)

 

r = r + y[i][k]*z[k][j];

 

x[i][j] = x[i][j] + r;

 

};

 

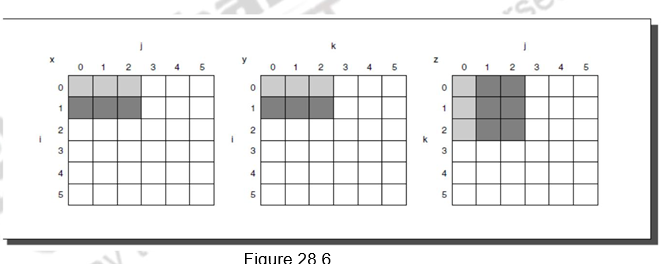
Figure 28.6 illustrates the accesses to the three arrays using blocking. Looking only at capacity misses, the total number of memory words accessed is 2N3/B + N2. This total is an improvement by about a factor of B. Hence, blocking exploits a combination of spatial and temporal locality, since y benefits from spatial locality and z benefits from temporal locality.

 

Although we have aimed at reducing cache misses, blocking can also be used to help register allocation. By taking a small blocking size such that the block can be held in registers, we can minimize the number of loads and stores in the program.

 

To summarize, we have defined the average memory access time in this module. The AMAT depends on the hit time, miss rate and miss penalty. Several optimizations exist to handle each of these factors. We discussed five different techniques for reducing the miss rates. They are: