31 Other Issues with Parallel Processors
Dr A. P. Shanthi
The objectives of this module are to discuss about the synchronization issues present in multi-processors and also give an introduction to the various memory consistency models.
We have so far discussed about the various cache coherency protocols that are used to maintain cache coherency in multi-processor systems. But, apart from the cache coherency problem, there are other issues to be handled in a multi-processor system. We shall discuss about them in this module.
In a multi-processor system, where data is being shared by multiple processors, we need to provide synchronization to know when it is safe for different processes to use shared data. In the case of communication through message passing, there is explicit coordination with transmission or arrival of data . However, when communication is through shared address space, additional operations to explicitly coordinate the sharing of data between the various processors are required. For example, enabling a flag, awakening a thread, interrupting a processor, etc. may be required.
Normally, the hardware provides some synchronization primitives and we have software synchronization routines/libraries built based on them. In small scale systems, the most primitive support provided by the hardware is an uninterruptible instruction or an instruction sequence that can atomically retrieve the contents of a memory location and also change it. Software synchronization mechanisms are then constructed using this capability. In larger-scale multiprocessors or high-contention situations, synchronization can become a performance bottleneck because contention introduces additional delays and because latency is potentially greater in such a multiprocessor.
Basic Hardware Primitives: The primary hardware support is the ability to retrieve and change the contents of a memory location. This can be achieved with an atomic exchange, which interchanges a value in a register for a value in memory. Let us assume that we want to build a simple lock, where the value 0 is used to indicate that the lock is free and 1 is used to indicate that the lock is unavailable. A processor tries to set the lock by doing an exchange of 1, which is in a register, with the memory address, which is corresponding to the lock. The value returned from the exchange instruction is 1 if some other processor had already claimed access, and 0 otherwise. In the latter case, the value is also changed to 1, preventing any competing exchange from also retrieving a 0.
For example, consider two processors that each try to do the exchange simultaneously. This race is broken since exactly one of the processors will perform the exchange first, returning 0, and the second processor will return 1 when it does the exchange. The key to using the exchange (or swap) primitive to implement synchronization is that the operation is atomic. The exchange is indivisible, and two simultaneous exchanges will be ordered by the write serialization mechanisms. It is impossible for two processors trying to set the synchronization variable in this manner to assume that have simultaneously set the variable.
Yet another operation, present in many older multiprocessors, is test-and-set, which tests a value and sets it if the value passes the test. For example, an operation that tests for 0 and sets the value to 1 can be used. This is similar to the atomic exchange discussed earlier. Another atomic synchronization primitive is fetch-and-increment. It returns the value of a memory location and atomically increments it. By using the value 0 to indicate that the synchronization variable is unclaimed, we can use fetch-and-increment, just as we used exchange.
However, implementing a single atomic memory operation introduces some challenges, since it requires both a memory read and a write in a single, uninterruptible instruction. This requirement complicates the implementation of coherence, since the hardware cannot allow any other operations between the read and the write, and yet must not deadlock. An alternative is to have a pair of instructions where the second instruction returns a value from which it can be deduced whether the pair of instructions was executed as if the instructions were atomic. The pair of instructions is said to be atomic if it appears as if all other operations executed by any processor occurred before or after the pair. The pair of instructions includes a special load called a load linked or load locked and a special store called a store conditional. These instructions are used in sequence. If the contents of the memory location specified by the load linked are changed before the store conditional to the same address occurs, then the store conditional fails. If the processor does a context switch between the two instructions, then also the store conditional fails. The store conditional is defined to return 1 if it was successful and a 0 otherwise. Since the load linked returns the initial value and the store conditional returns 1 only if it succeeds, the following sequence implements an atomic exchange on the memory location specified by the contents of R1:
try: MOV R3,R4 ;mov exchange value
LL R2,0(R1) ;load linked
SC R3,0(R1) ;store conditional
BEQZ R3,try ;branch store fails
MOV R4,R2 ;put load value in R4
At the end of this sequence the contents of R4 and the memory location specified by R1 have been atomically exchanged. Any time a processor intervenes and modifies the value in memory between the LL and SC instructions, the SC returns 0 in R3, causing the code sequence to try again.
Similarly, the following example shows how we can implement a fetch &

These instructions are typically implemented by keeping track of the address specified in the LL instruction in a register, called the link register. If an interrupt occurs, or if the cache block matching the address in the link register is invalidated, for example, by another SC, the link register is cleared. The SC instruction simply checks that its address matches that in the link register. If so, the SC succeeds; otherwise, it fails. Since the store conditional will fail after either another attempted store to the load linked address or any exception, we must be careful in choosing what instructions are inserted between the two instructions. In particular, only register-register instructions can safely be permitted. Otherwise, it is possible to create deadlock situations where the processor can never complete the SC. In addition, the number of instructions between the load linked and the store conditional should be small to minimize the probability that either an unrelated event or a competing processor causes the store conditional to fail frequently.
Implementing Spin Locks: Once the atomic exchange primitive is available, we can implement a spin lock using this. A spin lock is one, wherein the processor keeps spinning for a lock, until it becomes available. This is normally used when we expect the lock to be held only for a short duration and the process of acquiring the lock itself does not consume too much time. Otherwise, the processor keeps waiting for a long time. Consider the following code sequence, assuming the lock variables are available in memory:
DADDUI R2, R0, #1
lockit: EXCH R2, 0(R1) ;atomic exchange
BNEZ R2, lockit ;already locked?
Here, we use the atomic exchange instruction. If the exchange happens successfully, R2 will have a value of 0. If R2 has a value of 1, the processor knows that the lock was not acquired, and starts spinning again.
If the multiprocessor system supports cache coherence, we can cache the locks using the coherence mechanism to maintain the lock value coherently. Caching locks has two advantages. First, the process of spinning could be done on a local cached copy rather than requiring a global memory access on each attempt to acquire the lock. The second advantage is because of the fact that there is often locality in lock accesses. That is, the processor that used the lock last will use it again in the near future. In such cases, the lock value may reside in the cache of that processor, greatly reducing the time to acquire the lock. We, accordingly, modify our spin lock procedure. The reads are done on the local copy, and only if the processor knows that the lock is available, it attempts to acquire the lock using a swap. This avoids the number of writes on the shared data. The winning processor executes the code after the lock and, when finished, stores a 0 into the lock variable to release the lock, which starts the race all over again. The following code illustrates the idea:
lockit: LD R2, 0(R1) ; load of lock
BNEZ R2, lockit ; not available-spin
DADDUI R2, R0, #1; load locked value
EXCH R2, 0(R1) ; swap
BNEZ R2, lockit ; branch if lock was not 0
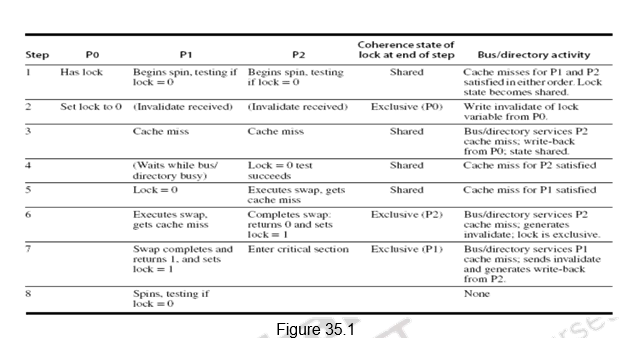
The spin lock mechanism using cache coherence is illustrated in Figure 35.1. Processor P0 has the lock and P1 and P2 are reading the lock status. So, the lock status becomes shared. One of them will be serviced first. When processor P0 releases the lock, it invalidates all other caches. They must fetch the new value to update their copy of the lock. One such cache gets the copy of the unlocked value (0) first and performs the swap. When the cache miss of other processors is satisfied, they find that the variable is already locked, so they must return to testing and spinning.
Barrier Sychronization: Next we shall look at how barrier synchronization is implemented. Barriers are synchronization primitives that ensure that some processes do not outrun others – if a process reaches a barrier, it has to wait until every process reaches the barrier. When a process reaches a barrier, it acquires a lock and increments a counter that tracks the number of processes that have reached the barrier. It then spins on a value that gets set by the last arriving process. This ensures that the processes are allowed to exit the barrier only when all the processes have reached t he barrier.

Figure 35.2 shows how barrier synchronization can be implemented. The first processor entering the barrier resets the release and increments the count. As each processor enters the barrier it acquires the lock for count and increments the count value. Once count becomes equal to total, indicating that all the processes have reached the barrier, the barrier is released. Till the count is satisfied, all the processes keep spinning.
But, we have a problem here. If we have two processes, one fast and the other slow. The slow process arrives first, reads release, sees 0 and waits. The fast process arrives, sets release to 1, goes on to execute other code, comes to barrier again, resets release, and starts spinning. The slow now reads release again, sees 0 again and gets stuck. Now, both the processes are stuck and will never leave.
This can be overcome by either counting on the number of processes leaving also, or using a sense-reversing barrier as shown in Figure 35.3. The release in the first barrier acts as the reset for the second. When the fast process comes back, it does not change release, it just waits for it to become 0. The slow eventually sees release is 1, stops spinning, does work, comes back, sets release to 0, and both go forward.
There are many more synchronizations possible. We have discussed only the most primitive ones.

An Introduction to Memory Consistency Models: Another important issue to be handled with multi-processors is memory consistency. We had already outlined the problem in an earlier module. Cache coherence ensures that multiple processors see a consistent view of memory. But, when must a processor see a value that has been updated by another processor, is a question. Since processors communicate through shared variables, the order in which a processor observes the data writes of another processor is important. Since the writes of another processor can only be observed through reads, we will have to decide on the properties that must be enforced among reads and writes to different locations by different processors.
As an example, observe the code sequence below. Here are two code segments from processes P1 and P2:

Assume that the processes are running on different processors, and that locations A and B are originally cached by both processors with the initial value of 0. If writes always take immediate effect and are immediately seen by other processors, it will be impossible for both if statements to evaluate their conditions as true. But suppose the write invalidate is delayed, and the processor is allowed to continue during this delay; then it is possible that both P1 and P2 have not seen the invalidations for B and A before they attempt to read the values. There is an ambiguity about what the programmer had in mind and what is actually happening. Consistency models clarify on these issues. The consistency model defines the ordering of writes and reads to different memory locations. The hardware guarantees a certain consistency model and the programmer attempts to write correct programs with those assumptions.
The most straightforward model for memory consistency is called sequential consistency. Sequential consistency requires that the result of any execution be the same as if the memory accesses executed by each processor were kept in order and the accesses among different processors were arbitrarily interleaved. Sequential consistency eliminates the possibility of some non obvious execution in the previous example because the assignments must be completed before the if statements are initiated.
The simplest way to implement sequential consistency is to require a processor to delay the completion of any memory access until all the invalidations caused by that access are completed. The next memory access has to be delayed until the previous one is completed. Memory consistency involves operations among different variables. The two accesses that must be ordered are actually to different memory locations. We must delay the read of A or B (A = 0 or B = 0) until the previous write has completed (B= 1 or A = 1). Under sequential consistency, we cannot place the write in a write buffer and continue with the read.
Sequential consistency is very easy to understand and presents a very simple programming model. However, it does not allow many of the optimizations and so the performance will get affected. It is the simplest, yet the strictest consistency model. A better implementation would be for the processor to issue accesses as it sees fit, but detect and fix potential violations of sequential consistency.
The challenge lies in developing a programming model that is simple and at the same time gives good performance. For example, we can assume that programs are synchronized, wherein all access to shared data are ordered by synchronization operations that we discussed earlier. A data reference is ordered by a synchronization operation if, in every possible execution, a write of a variable by one processor and an access (either a read or a write) of that variable by another processor are separated by a pair of synchronization operations, one executed after the write by the writing processor and one executed before the access by the second processor. In case of variables being updated without ordering by synchronization, this will lead to data races because the execution outcome depends on the relative speed of the processors and the outcome is unpredictable. So, we need to write synchronized programs that are data-race-free.
Programmers can write their own synchronization mechanisms, but this is not guaranteed to work and can lead to buggy programs. Therefore, typically all programmers will choose to use synchronization libraries that are correct and optimized for the multiprocessor and the type of synchronization. Also, the use of standard synchronization primitives ensures that even if the architecture implements a more relaxed consistency model than sequential consiste ncy, a synchronized program will behave as if the hardware implemented sequential consistency.
Relaxed Consistency Models: The key idea in relaxed consistency models is to allow reads and writes to complete out of order, but to use synchronization operations to enforce ordering, so that a synchronized program behaves as if the processor were sequentially consistent. There are a variety of relaxed models that are classified according to what read and write orderings they relax. Sequential consistency constraints can be relaxed in the following ways (allowing higher performance):
- within a processor, a read can complete before an earlier write to a different memory location completes
- within a processor, a write can complete before an earlier write to a different memory location completes
- within a processor, a read or write can complete before an earlier read to a different memory location completes
- a processor can read the value written by another processor before all processors have seen the invalidate
- a processor can read its own write before the write is visible to other processors
We specify the orderings by a set of rules of the form X→Y, meaning that operation X must complete before operation Y is done. Sequential consistency requires maintaining all four possible orderings: R→W, R→R, W→R, and W→W. The relaxed models are defined by which of these four sets of orderings they relax:
- Relaxing the W→R ordering yields a model known as total store ordering or processor consistency. Because this ordering retains ordering among writes, many programs that operate under sequential consistency operate under this model, without additional synchronization.
- Relaxing the W→W ordering yields a model known as partial store order.
- Relaxing the R→W and R→R orderings yields a variety of models including weak ordering, the PowerPC consistency model, and release consistency, depending on the details of the ordering restrictions and how synchronization operations enforce ordering.
Thus, by relaxing different orderings, the processor can possibly obtain significant performance advantages.
To summarize, we have discussed the synchronization issues associated with multi-processors. We have discussed the primitive atomic exchange instruction supported by the hardware and looked at how this can be used to build various synchronization primitives like simple locks, spin locks and barrier synchronization. We also had an introduction to memory consistency models.
Web Links / Supporting Materials
- Computer Architecture – A Quantitative Approach , John L. Hennessy and David A.Patterson, 5th Edition, Morgan Kaufmann, Elsevier, 2011.